蓝桥杯DFS专题
2016-C-7 寒假作业
刷题链接: link.
现在小学的数学题目也不是那么好玩的。
看看这个寒假作业:
□ + □ = □
□ - □ = □
□ × □ = □
□ ÷ □ = □
(如果显示不出来,可以参见【图1.jpg】)
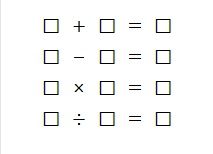
每个方块代表1~13中的某一个数字,但不能重复。
比如:
6 + 7 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
以及:
7 + 6 = 13
9 - 8 = 1
3 * 4 = 12
10 / 2 = 5
就算两种解法。(加法,乘法交换律后算不同的方案)
你一共找到了多少种方案?
请填写表示方案数目的整数。
注意:你提交的应该是一个整数,不要填写任何多余的内容或说明性文字。
注意:该题全排列会超时。
我的代码:
#include
int count=0;
int a[15],vis[15];
void dfs(int n)
{
if(n==3)
{
if(a[0]+a[1]!=a[2])
return;
}
if(n==6)
{
if(a[3]-a[4]!=a[5])
return;
}
if(n==9)
{
if(a[6]*a[7]!=a[8])
return;
}
if(n==12)
{
if(a[10]*a[11]==a[9])
count++;
return;
}
for(int i=1;i<=13;i++)
{
if(vis[i]==0)
{
vis[i]=1;
a[n]=i;
dfs(n+1);
vis[i]=0;
}
}
}
using namespace std;
int main()
{
dfs(0);
printf("%d",count);
return 0;
}
参考代码:
#include
int count=0;
int v[15],a[15];
void dfs(int n)
{
if(n==3)
{
if(a[0]+a[1]!=a[2])
return;
}
if(n==6)
{
if(a[3]-a[4]!=a[5])
return;
}
if(n==9)
{
if(a[6]*a[7]!=a[8])
return;
}
if(n==12)
{
if(a[10]*a[11]==a[9])
count++;
return;
}
for(int i=1;i<=13;i++)
{
if(v[i]==0)
{
v[i]=1;
a[n]=i;
dfs(n+1);
v[i]=0;
}
}
}
int main()
{
dfs(0);
printf("%d",count);
return 0;
}
2013-A-9 剪格子
刷题链接: link.
如图p1.jpg所示,3 x 3 的格子中填写了一些整数。
我们沿着图中的红色线剪开,得到两个部分,每个部分的数字和都是60。
本题的要求就是请你编程判定:对给定的m x n 的格子中的整数,是否可以分割为两个部分,使得这两个区域的数字和相等。
如果存在多种解答,请输出包含左上角格子的那个区域包含的格子的最小数目。
如果无法分割,则输出 0
程序输入输出格式要求:
程序先读入两个整数 m n 用空格分割 (m,n<10)
表示表格的宽度和高度
接下来是n行,每行m个正整数,用空格分开。每个整数不大于10000
程序输出:在所有解中,包含左上角的分割区可能包含的最小的格子数目。
例如:
用户输入:
3 3
10 1 52
20 30 1
1 2 3
则程序输出:
3
再例如:
用户输入:
4 3
1 1 1 1
1 30 80 2
1 1 1 100
则程序输出:
10
(参见p2.jpg)
思路:dfs
我的代码:
#include
#include
#include
using namespace std;
int m,n,count=0;
int a[10][10],vis[15][10];
int MOVE[2][4]={{1,-1,0,0},{0,0,1,-1}};
long long sum=0,ans=0;
int cnt=99999;
void dfs(int x,int y,int k)
{
/*if(vis[x][y]==1)
return;*/
if(x<0||y<0||x>=n||y>=m)
return;
if(sum-ans==ans)
{
cnt=min(cnt,k);
return;
}
for(int i=0;i<4;i++)
{
int tx=x+MOVE[0][i];
int ty=y+MOVE[1][i];
if(vis[x][y]==0)
{
vis[x][y]=1;
ans+=a[x][y];
k++;
dfs(tx,ty,k);
k--;
ans-=a[x][y];
vis[x][y]=0;
}
}
}
using namespace std;
int main()
{
scanf("%d%d",&m,&n);
for(int i=0;i 参考代码:
#include
#include
#include
#include
using namespace std;
int a[10][10];
bool vis[10][10];
int n,m,cnt=99999;
int MOVE[2][4]={{0,1,0,-1},{1,0,-1,0}};
long long sum=0,ans=0;
void dfs(int x,int y,int k)
{
if(vis[x][y]==true)
return;
if(x>=n||x<0||y>=m||y<0)
return;
if(sum-ans==ans)
{
cnt=min(cnt,k);
return;
}
for(int i=0;i<4;i++)
{
int tx=x+MOVE[0][i];
int ty=y+MOVE[1][i];
vis[x][y]=true;
ans+=a[x][y];
k++;
dfs(tx,ty,k);
k--;
ans-=a[x][y];
vis[x][y]=false;
}
}
int main()
{
scanf("%d%d",&m,&n);
for(int i=0;i 2017-A-4 方格分割
刷题链接: link.
6x6的方格,沿着格子的边线剪开成两部分。
要求这两部分的形状完全相同。
如图:p1.png, p2.png, p3.png 就是可行的分割法。
试计算:
包括这3种分法在内,一共有多少种不同的分割方法。
注意:旋转对称的属于同一种分割法。
请提交该整数,不要填写任何多余的内容或说明文字。
我的代码:
#include
using namespace std;
int count=0;
int MOVE[2][4]={{1,-1,0,0},{0,0,1,-1}};
int vis[10][10];
void dfs(int x,int y)
{
if(x<=0||x>=6||y<=0||y>=6)
{
count++;
return;
}
for(int i=0;i<4;i++)
{
int tx=x+MOVE[0][i];
int ty=y+MOVE[1][i];
if(vis[x][y]==0&&vis[6-x][6-y]==0)
{
vis[x][y]=1;
vis[6-x][6-y]=1;
dfs(tx,ty);
vis[x][y]=0;
vis[6-x][6-y]=0;
}
}
}
int main()
{
dfs(3,3);
printf("%d",count/4);
return 0;
}
参考代码(dfs解题):
#include
#include
using namespace std;
int vis[10][10]={0};
int count=0;
void dfs(int x,int y)
{
int move[2][4]={{1,-1,0,0},{0,0,-1,1}};
if(x<=0||x>=6||y<=0||y>=6)
{
count++;
return;
}
for(int i=0;i<4;i++)
{
int tx=x+move[0][i];
int ty=y+move[1][i];
if(vis[tx][ty]==0&&vis[6-tx][6-ty]==0)
{
vis[tx][ty]=1;
vis[6-tx][6-ty]=1;
dfs(tx,ty);
vis[tx][ty]=0;
vis[6-tx][6-ty]=0;
}
}
}
int main()
{
vis[3][3]=1;
dfs(3,3);
printf("%d",count/4);
return 0;
}
2017-A-1 迷宫
刷题链接: link.
X星球的一处迷宫游乐场建在某个小山坡上。
它是由10x10相互连通的小房间组成的。
房间的地板上写着一个很大的字母。
我们假设玩家是面朝上坡的方向站立,则:
L表示走到左边的房间,
R表示走到右边的房间,
U表示走到上坡方向的房间,
D表示走到下坡方向的房间。
X星球的居民有点懒,不愿意费力思考。
他们更喜欢玩运气类的游戏。这个游戏也是如此!
开始的时候,直升机把100名玩家放入一个个小房间内。
玩家一定要按照地上的字母移动。
迷宫地图如下:
UDDLUULRUL
UURLLLRRRU
RRUURLDLRD
RUDDDDUUUU
URUDLLRRUU
DURLRLDLRL
ULLURLLRDU
RDLULLRDDD
UUDDUDUDLL
ULRDLUURRR
请你计算一下,最后,有多少玩家会走出迷宫?
而不是在里边兜圈子。
请提交该整数,表示走出迷宫的玩家数目,不要填写任何多余的内容。
如果你还没明白游戏规则,可以参看一个简化的4x4迷宫的解说图:p1.png
我的代码:
#include
#include
using namespace std;
char a[15][15];
int vis[15][15];
int count=0;
int cnt=0;
void dfs(int x,int y)
{
memset(vis,0,sizeof(vis));
while(1)
{
if(x<0||x>9||y<0||y>9)
{
count++;
return;
}
if(vis[x][y]==1)
return;
vis[x][y]=1;
switch(a[x][y])
{
case 'U':x--;break;
case 'D':x++;break;
case 'L':y--;break;
case 'R':y++;break;
default:break;
}
}
}
int main()
{
for(int i=0;i<10;i++)
for(int j=0;j<10;j++)
scanf(" %c",&a[i][j]);
for(int i=0;i<10;i++)
for(int j=0;j<10;j++)
dfs(i,j);
printf("%d",count);
return 0;
}
参考代码(dfs解题)
#include
#include
using namespace std;
char map[20][20];
int vis[20][20];
int dfs(int i,int j)
{
memset(vis,0,sizeof(vis));
while(1)
{
if(i<0||i>9||j<0||j>9)
return 1;
if(vis[i][j])
return 0;
vis[i][j]=1;
switch(map[i][j])
{
case 'U':i--;break;
case 'D':i++;break;
case 'L':j--;break;
case 'R':j++;break;
default:break;
}
}
}
int main()
{
int count=0;
for(int i=0;i<10;i++)
for(int j=0;j<10;j++)
scanf(" %c",&map[i][j]);
//加空格可以吃掉回车
for(int i=0;i<10;i++)
for(int j=0;j<10;j++)
count=count+dfs(i,j);
printf("%d",count);
return 0;
}
对称迷宫
刷题链接: link.
用EXCEL求解迷宫真香~
wlxsq有一个N*NN∗N的网格迷宫,每一个网格都有一个字母编号。
他要从左上角(1,1)(1,1)出发,走到右下角(n,n)(n,n),由于wlxsq很懒,所以他每次只会往右或者往下走一格。
由于最后到终点的路径方案太多太多了,所以wlxsq想让你计算出所有不同的对称的路径个数。
例如:N = 3 N=3
ABA
BBB
ABA
对称路径6条:有ABABA(2条)、ABBBA(4条)
不同的对称路径有: 有ABABA、ABBBA
输入
第一行输入一个数NN,表示迷宫的大小。
接下来输入N*NN∗N的字母迷宫
输出
输出对称路径的数量
样例
输入复制
3
ABA
BBB
ABA
输出复制
2
提示
【评测用例规模与约定】
对于40%40%的数据,2<=N<=112<=N<=11
对于100%100%的数据,2<=N<=182<=N<=18
思路:双DFS
我的代码:
#include
#include
#include 参考代码:
#include
#include
#include
#include 




