LeetCode_Array_300. Longest Increasing Subsequence 最长递增子序列【动态规划】【Java】【中等】

目录

一，题目描述

英文描述

中文描述

示例与说明

二，解题思路

三，AC代码

Java

四，解题过程

第一搏

第二搏

---

 

一，题目描述

英文描述

Given an integer array nums, return the length of the longest strictly increasing subsequence.

A subsequence is a sequence that can be derived from an array by deleting some or no elements without changing the order of the remaining elements. For example, [3,6,2,7] is a subsequence of the array [0,3,1,6,2,2,7].

中文描述

给你一个整数数组 nums ，找到其中最长严格递增子序列的长度。

子序列 是由数组派生而来的序列，删除（或不删除）数组中的元素而不改变其余元素的顺序。例如，[3,6,2,7] 是数组 [0,3,1,6,2,2,7] 的子序列。

示例与说明

来源：力扣（LeetCode）
链接：https://leetcode-cn.com/problems/longest-increasing-subsequence
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

二，解题思路

只想到了O(N^2)的动态规划解法，贪心+二分查找O(NlogN)的解法看不懂┗( T﹏T )┛

开一个数组record，记录每一个位置最终答案。

从前往后遍历原始数组nums，计算当前位置 i 最终答案时，需要遍历record数组之前所有小于nums[i]的记录，计算并更新record[i]。

 

三，AC代码

Java

class Solution {
    public int lengthOfLIS(int[] nums) {
        int len = nums.length;
        int[] record = new int[len];
        int ans = 1;
        for (int i = 0; i < len; i++) {
            record[i] = 1;
        }
        for (int i = 1; i < len; i++) {
            for (int j = i - 1; j >= 0; j--) {
                if (nums[i] > nums[j]) {
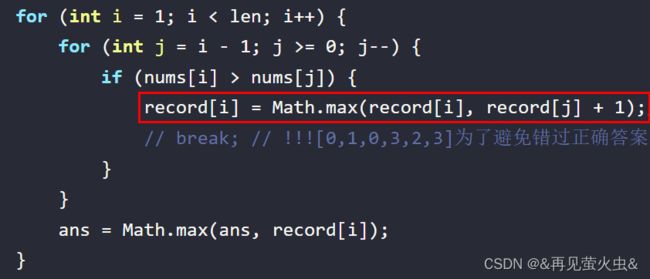
                    record[i] = Math.max(record[i], record[j] + 1);// !!![0,1,0,3,2,3]
                    // break; // !!![0,1,0,3,2,3]为了避免错过正确答案，需要遍历全部，不能中途break
                }
            }
            ans = Math.max(ans, record[i]);
        }
        return ans;
    }
}

四，解题过程

第一搏

开一个数组record，记录每一个位置最终答案。

从前往后遍历原始数组nums，计算当前位置 i 最终答案时，需要遍历record数组之前所有小于nums[i]的记录，计算并更新record[i]。这么说有点绕，直接上代码：

class Solution {
    public int lengthOfLIS(int[] nums) {
        int len = nums.length;
        int[] record = new int[len];
        int ans = 1;
        // 先把record中初始为1
        for (int i = 0; i < len; i++) {
            record[i] = 1;
        }
        for (int i = 1; i < len; i++) {
            for (int j = i - 1; j >= 0; j--) {
                if (nums[i] > nums[j]) {
                    record[i] = Math.max(record[i], record[j] + 1);// !!![0,1,0,3,2,3]
                    // break; // !!![0,1,0,3,2,3]为了避免错过正确答案，需要遍历全部，不能中途break
                }
            }
            ans = Math.max(ans, record[i]);
        }
        return ans;
    }
}

一开始想偷懒，j从后向前遍历时，遇到第一个小于nums[i]的就跳出来，以[0,1,0,3,2,3]为例

当i为4，即nums[i]=2时，j从3向前遍历，遇到第一个nums[j] < nums[i]=2时，更新record[i]=record[j]+1，然后跳出循环，i++，此时j=2，即nums[j]=0，record[j]=1。

但实际上j继续向左遍历时，j=1时，record[j]=2，这时计算record[i]=3，这样就错过了正确答案。

所以j还是采用从后向前全部遍历的方法，算法整体时间复杂度O(N^2)

第二搏

基于贪心+二分查找。看了好多题解，但是还没看明白┗( T﹏T )┛