精简版->优化版|01背包、完全背包、多重背包
背包问题
01背包问题
有n个物品,它们有各自的体积w和价值v,现有给定容量W的背包,在总体积不超过背包承载上限的情况下,如何让背包里装入的物品具有最大的价值总和?(每个物品最多可使用一次)
w(i) 表示第i个物品的体积,v(i) 表示第i个物品的价值,
dp[i,j] : 当前背包容量为j,前i个物品最佳组合对应的价值。
不装入第i个商品,则dp[i,j] = dp[i-1, j],
装入第i个商品, 则dp[i,j] = dp[i-1, j-w(i)] + v(i),
dp[i,j] = max{dp[i-1, j], dp[i-1, j-w(i)] + v(i)} j>=w(i).
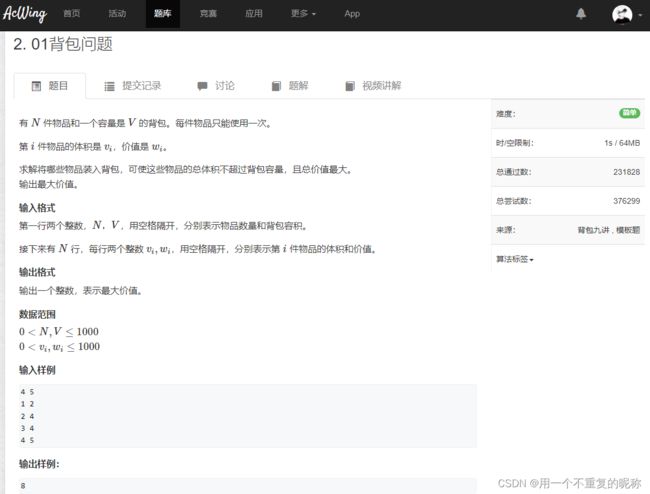
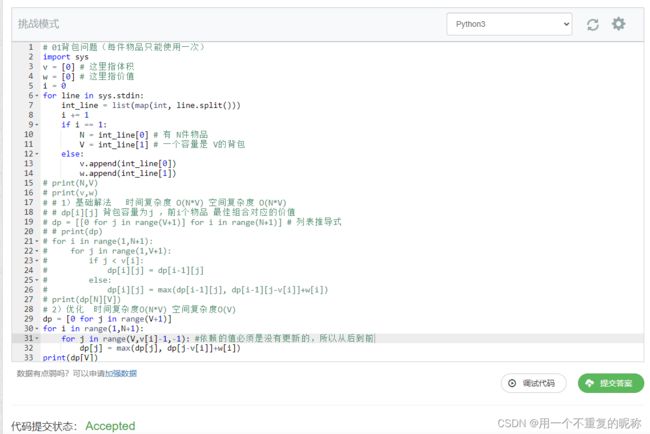
网站: https://www.acwing.com/problem/content/3/
# 01背包问题(每件物品只能使用一次)
import sys
v = [0] # 这里指体积
w = [0] # 这里指价值
i = 0
for line in sys.stdin:
int_line = list(map(int, line.split()))
i += 1
if i == 1:
N = int_line[0] # 有 N件物品
V = int_line[1] # 一个容量是 V的背包
else:
v.append(int_line[0])
w.append(int_line[1])
# print(N,V)
# print(v,w)
# # 1)基础解法 时间复杂度 O(N*V) 空间复杂度 O(N*V)
# # dp[i][j] 背包容量为j ,前i个物品 最佳组合对应的价值
# dp = [[0 for j in range(V+1)] for i in range(N+1)] # 列表推导式
# # print(dp)
# for i in range(1,N+1):
# for j in range(1,V+1):
# if j < v[i]:
# dp[i][j] = dp[i-1][j]
# else:
# dp[i][j] = max(dp[i-1][j], dp[i-1][j-v[i]]+w[i])
# print(dp[N][V])
# 2)优化 时间复杂度O(N*V) 空间复杂度O(V)
dp = [0 for j in range(V+1)]
for i in range(1,N+1):
for j in range(V,v[i]-1,-1):
dp[j] = max(dp[j], dp[j-v[i]]+w[i])
print(dp[V])
01背包问题最优解回溯 https://blog.csdn.net/qq_37767455/article/details/99086678
完全背包问题
有n种物品和一个容量为W的背包,第i种物品的体积是w(i),价值是v(i)。在总体积不超过背包承载上限的情况下,求解将哪些物品装入背包,可使这些物品的总价值最大。(每种物品都有无限件可用)
从装入第i种物品多少件出发,01背包只有两种情况即取0件和取1件,而这里是取0件、1件、2件…直到超过限重(k>j/w(i))
dp[i][j] : 当前背包容量为j,前i个物品最佳组合对应的价值。
#k为装入第i种物品的件数,k<=j/w(i)
dp[i][j] = max{ (dp[i-1][j- kw(i)] + kv(i) ) for every k }
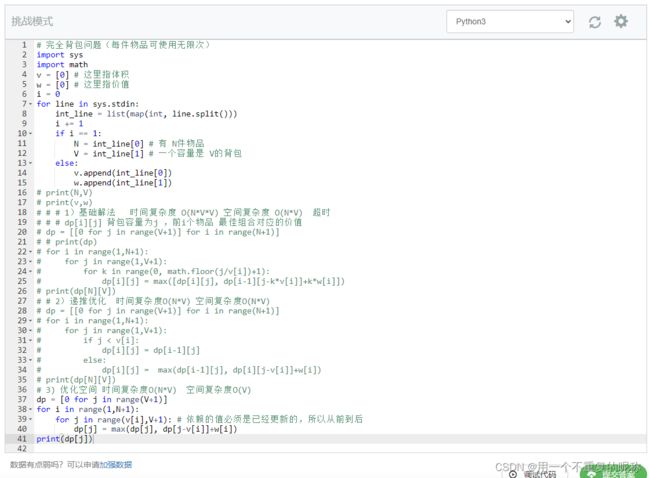

【参考】
http://jjzhong.com/2022/11/29/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E5%8F%8A%E5%85%B6%E4%BC%98%E5%8C%96/ 时间复杂度、空间复杂度
https://juejin.cn/post/7181264109470482488 看起来很详细的教程
【题解】https://www.acwing.com/solution/content/87389/ 包含递推、二进制优化等
# 完全背包问题(每件物品可使用无限次)
import sys
import math
v = [0] # 这里指体积
w = [0] # 这里指价值
i = 0
for line in sys.stdin:
int_line = list(map(int, line.split()))
i += 1
if i == 1:
N = int_line[0] # 有 N件物品
V = int_line[1] # 一个容量是 V的背包
else:
v.append(int_line[0])
w.append(int_line[1])
# print(N,V)
# print(v,w)
# # # 1)基础解法 时间复杂度 O(N*V*V) 空间复杂度 O(N*V) 超时
# # # dp[i][j] 背包容量为j ,前i个物品 最佳组合对应的价值
# dp = [[0 for j in range(V+1)] for i in range(N+1)]
# # print(dp)
# for i in range(1,N+1):
# for j in range(1,V+1):
# for k in range(0, math.floor(j/v[i])+1):
# dp[i][j] = max([dp[i][j], dp[i-1][j-k*v[i]]+k*w[i]])
# print(dp[N][V])
# # 2)递推优化 时间复杂度O(N*V) 空间复杂度O(N*V)
# dp = [[0 for j in range(V+1)] for i in range(N+1)]
# for i in range(1,N+1):
# for j in range(1,V+1):
# if j < v[i]:
# dp[i][j] = dp[i-1][j]
# else:
# dp[i][j] = max(dp[i-1][j], dp[i][j-v[i]]+w[i])
# print(dp[N][V])
# 3) 优化空间 时间复杂度O(N*V) 空间复杂度O(V)
dp = [0 for j in range(V+1)]
for i in range(1,N+1):
for j in range(v[i],V+1): # 依赖的值必须是已经更新的,所以从前到后
dp[j] = max(dp[j], dp[j-v[i]]+w[i])
print(dp[j])
多重背包问题
有n种物品和一个容量为W的背包,第i种物品的数量为s(i),体积是w(i),价值是v(i)。在总体积不超过背包承载上限的情况下,求解将哪些物品装入背包,可使这些物品的总价值最大。(每种物品的数量有限制)
从装入第i种物品多少件出发,取0件、1件、2件…s(i)件,还要满足不超过限重。
dp[i][j]: 当前背包容量为j,前i个物品最佳组合对应的价值。
#k为装入第i种物品的件数,k<= min{ s(i), j/w(i)}
dp[i][j] = max{ (dp[i-1][j-kw(i)] + kv(i)) for every k}
# 多重背包问题(每种物品的数量有限制)
import sys
import math
v = [0] # 这里指体积
w = [0] # 这里指价值
s = [0] # 数量限制
i = 0
for line in sys.stdin:
int_line = list(map(int, line.split()))
i += 1
if i == 1:
N = int_line[0] # 有 N件物品
V = int_line[1] # 一个容量是 V的背包
else:
v.append(int_line[0])
w.append(int_line[1])
s.append(int_line[2])
# # # # 1)基础解法 时间复杂度 O(N*V*S) 空间复杂度 O(N*V) 超时
# # # # dp[i][j] 背包容量为j ,前i个物品 最佳组合对应的价值
# dp = [[0 for j in range(V+1)] for i in range(N+1)]
# # print(dp)
# for i in range(1,N+1):
# for j in range(0,V+1):
# for k in range(0, min([math.floor(j/v[i])+1, s[i]+1])):
# dp[i][j] = max([dp[i][j], dp[i-1][j-k*v[i]]+k*w[i]])
# print(dp[N][V])
# 2) 二进制优化 把时间复杂度从朴素写法的 O(N*V*S) 优化为 O(N*logS*V)
new_v = [0] * (11 * 1000 + 1) # 2000件物品需要分11堆,最多有N=1000种物品
new_w = [0] * (11 * 1000 + 1)
cnt = 0 # 分的堆数
for i in range(1,N+1): # N*logS
k = 1
while(s[i]>=k):
cnt += 1
new_v[cnt] = v[i]*k
new_w[cnt] = w[i]*k
s[i] -= k
k = k * 2
if s[i] > 0 :
cnt += 1
new_v[cnt] = v[i]*s[i]
new_w[cnt] = w[i]*s[i]
dp = [0 for j in range(V+1)]
for i in range(1,cnt+1): # N*logS*V
for j in range(V,new_v[i]-1,-1): # 01背包的空间优化
dp[j] = max([dp[j], dp[j-new_v[i]]+new_w[i]])
print(dp[V])
# https://www.acwing.com/solution/content/87389/
https://juejin.cn/post/7181264109470482488 很完整的背包问题?
胡乱的参考链接-_-||
https://blog.csdn.net/woomay/article/details/133162560?spm=1001.2014.3001.5501
https://blog.csdn.net/weixin_41082481/article/details/115922389?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2defaultBlogCommendFromBaiduRate-1-115922389-blog-72900009.235%5Ev38%5Epc_relevant_default_base3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2defaultBlogCommendFromBaiduRate-1-115922389-blog-72900009.235%5Ev38%5Epc_relevant_default_base3&utm_relevant_index=2
动态规划-背包问题
https://blog.csdn.net/qq_37767455/article/details/99086678
https://zhuanlan.zhihu.com/p/93857890
https://blog.csdn.net/qq_38410730/article/details/81667885
【动态规划】01背包问题(通俗易懂,超基础讲解)
https://www.zhihu.com/question/23995189 什么是动态规划(Dynamic Programming)?动态规划的意义是什么?
https://www.cnblogs.com/mhpp/p/7700235.html 动态规划初探及什么是无后效性? (转)
https://www.zdaiot.com/DataStructureAlgorithm/40%E5%8A%A8%E6%80%81%E8%A7%84%E5%88%92%E7%90%86%E8%AE%BA%EF%BC%9A%E4%B8%80%E7%AF%87%E6%96%87%E7%AB%A0%E5%B8%A6%E4%BD%A0%E5%BD%BB%E5%BA%95%E6%90%9E%E6%87%82%E6%9C%80%E4%BC%98%E5%AD%90%E7%BB%93%E6%9E%84%E3%80%81%E6%97%A0%E5%90%8E%E6%95%88%E6%80%A7%E5%92%8C%E9%87%8D%E5%A4%8D%E5%AD%90%E9%97%AE%E9%A2%98/
0动态规划理论:一篇文章带你彻底搞懂最优子结构、无后效性和重复子问题
https://blog.csdn.net/qq_30137611/article/details/77655707 什么是无后效性?
https://juejin.cn/post/6951922898638471181
看一遍就理解:动态规划详解
https://houbb.github.io/2020/01/23/data-struct-learn-07-base-dp#%E6%9C%80%E5%B0%8F%E8%B7%AF%E5%BE%84%E4%B9%8B%E5%92%8C
五大基本算法之动态规划算法
https://zhuanlan.zhihu.com/p/368901684?utm_campaign=&utm_medium=social&utm_oi=740423421275422720&utm_psn=1689458562500431873&utm_source=zhihu
https://www.zhihu.com/question/484180920/answer/2574186966?utm_campaign=&utm_medium=social&utm_oi=740423421275422720&utm_psn=1689463449510371328&utm_source=zhihu
https://seramasumi.github.io/docs/Algorithms/mc-%E5%BE%AE%E8%AF%BE%E5%A0%82-%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98.html
https://programmercarl.com/%E8%83%8C%E5%8C%85%E9%97%AE%E9%A2%98%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%80%E5%AE%8C%E5%85%A8%E8%83%8C%E5%8C%85.html#%E7%AE%97%E6%B3%95%E5%85%AC%E5%BC%80%E8%AF%BE
https://blog.csdn.net/qq_37767455/article/details/99086678
https://blog.csdn.net/Biteht/article/details/124298926?spm=1001.2014.3001.5501
数据结构与算法—算法篇之动态规划(一)
https://blog.csdn.net/chinawangfei/article/details/123585910?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-0-123585910-blog-99086678.235v38pc_relevant_sort_base3&spm=1001.2101.3001.4242.1&utm_relevant_index=1
背包问题之0-1背包算法详解
https://blog.csdn.net/char_m/article/details/107112564?utm_medium=distribute.pc_relevant.none-task-blog-2defaultbaidujs_baidulandingword~default-13-107112564-blog-99086678.235v38pc_relevant_sort_base3&spm=1001.2101.3001.4242.8&utm_relevant_index=14
https://blog.csdn.net/mu399/article/details/7722810
动态规划之01背包问题(最易理解的讲解)
https://github.com/youngyangyang04/leetcode-master/blob/master/problems/%E8%83%8C%E5%8C%85%E7%90%86%E8%AE%BA%E5%9F%BA%E7%A1%8001%E8%83%8C%E5%8C%85-1.md
https://zhuanlan.zhihu.com/p/93857890
动态规划之背包问题系列
https://blog.csdn.net/woshi250hua/article/details/7636866
【DP_背包专辑】【10.14最新更新】
https://blog.csdn.net/weixin_41082481/article/details/115922389?spm=1001.2101.3001.6650.1&utm_medium=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-1-115922389-blog-72900009.235%5Ev38%5Epc_relevant_default_base3&depth_1-utm_source=distribute.pc_relevant.none-task-blog-2%7Edefault%7EBlogCommendFromBaidu%7ERate-1-115922389-blog-72900009.235%5Ev38%5Epc_relevant_default_base3&utm_relevant_index=2
动态规划-背包问题