220217每日一题:力扣688.骑士在棋盘上的概率
题目
在一个 n x n 的国际象棋棋盘上,一个骑士从单元格 (row, column) 开始,并尝试进行 k 次移动。行和列是 从 0 开始 的,所以左上单元格是 (0,0) ,右下单元格是 (n - 1, n - 1) 。
象棋骑士有8种可能的走法,如下图所示。每次移动在基本方向上是两个单元格,然后在正交方向上是一个单元格。
每次骑士要移动时,它都会随机从8种可能的移动中选择一种(即使棋子会离开棋盘),然后移动到那里。
骑士继续移动,直到它走了 k 步或离开了棋盘。
返回 骑士在棋盘停止移动后仍留在棋盘上的概率 。
提示:
1 <= n <= 250 <= k <= 1000 <= row, column <= n
示例
输入: n = 3, k = 2, row = 0, column = 0
输出: 0.0625
解释: 有两步(到(1,2),(2,1))可以让骑士留在棋盘上。
在每一个位置上,也有两种移动可以让骑士留在棋盘上。
骑士留在棋盘上的总概率是0.0625。
输入: n = 1, k = 0, row = 0, column = 0
输出: 1.00000
解法一:暴力DFS
这道题目给我的第一反应是DFS暴力求解。通过递归统计所有可能的次数,并计算概率。由于每次棋子有8种可选移动方向(题目允许跳出棋盘),因此其总移动方案有8^k次。具体实现代码如下:
//解法一:暴力dfs
class Solution {
int[][] path = new int[][]{{1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}};
double possible = 0;
public double knightProbability(int n, int k, int row, int column) {
//计算所有可能总数
double sum = Math.pow(8,k);
dfs(n,k,row,column);
double t = possible;
return possible / sum;
}
public void dfs(int n,int k,int row,int col){
//如果已越界,返回
if(row >= n || col >= n || row < 0 || col < 0){
return;
}else{
//若步数走完,则自增
if(k == 0){
possible++ ;
return;
}else{
for(int i = 0;i<8;++i){
dfs(n,k - 1,row + path[i][0],col + path[i][1]);
}
}
}
}
}
自信提交,然而其执行结果如下:
11 / 22 个通过测试用例
状态:超出时间限制
提交时间:几秒前
最后执行的输入:
8 30 6 4
可以看见直接递归效率太低,因此考虑对算法进行优化。此外,由于k最大值能到100,因此简单使用Math.pow()计算其总路线数明显会导致数据溢出,需要进行处理。
解法二:DFS + 记忆搜索
分析实际案例发现在DFS搜索时对很多情况进行了重复计算,因此考虑使用记忆搜索减少运算量,优化算法(使用board[row][col][k]记录在row,col位置跳k次后还在棋盘上的概率),当board上有记录时,直接返回结果而不需要计算。针对概率问题,由于对棋子的第n次方向,八个方向的概率是相等的因此可以通过对每步直接计算其概率,避免数据溢出。其实现代码如下:
//解法二:dfs + 记忆搜索
class Solution {
int[][] path = new int[][]{{1,2},{1,-2},{-1,2},{-1,-2},{2,1},{2,-1},{-2,1},{-2,-1}};
//使用board[row][col][k]记录在row,col位置跳k次后还在棋盘上的概率
double[][][] board = new double[30][30][105];
double possible = 0;
public double knightProbability(int n, int k, int row, int column) {
//计算所有可能总数
return dfs(n,k,row,column);
}
public double dfs(int n,int k,int row,int col){
//如果已越界,返回
if(row >= n || col >= n || row < 0 || col < 0){
return 0;
}else{
//若步数走完,则自增
if(k == 0){
return 1;
}
if(board[row][col][k] != 0){
return board[row][col][k];
}else{
for(int i = 0;i<8;++i){
board[row][col][k] += dfs(n,k - 1,row + path[i][0],col + path[i][1]) * 0.125;
}
}
}
return board[row][col][k];
}
}
其执行代码如下:
22 / 22 个通过测试用例
状态:通过
执行用时: 7 ms
内存消耗: 42.5 MB
提交时间:1 小时前
解法三:动态规划
根据记忆搜索容易想到动态规划解法。需要找到其状态转移方程,考虑:
一个骑士有 8 种可能的走法,骑士会从中以等概率随机选择一种。部分走法可能会让骑士离开棋盘,另外的走法则会让骑士移动到棋盘的其他位置,并且剩余的移动次数会减少 1。
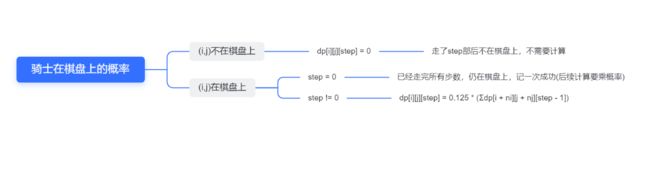
定义 dp[i][j][step] 表示骑士从棋盘上的点 (i, j)出发,走了 step 步时仍然留在棋盘上的概率。特别地,当点 (i, j) 不在棋盘上时dp[i][j][step]=0;当点 (i, j) 在棋盘上且 step=0 时,dp[i][j][step]=1。对于其他情况,dp[i][j][step]等于在step - 1步走到(i,j)的八个方向的概率和的1/8。其逻辑梳理如下:
其中(i+ni,j+nj)为与点(i,j)距离为一跳的八个坐标。其执行代码如下:
//解法三:动态规划
class Solution {
int[][] path = new int[][]{{-2, -1}, {-2, 1}, {2, -1}, {2, 1}, {-1, -2}, {-1, 2}, {1, -2}, {1, 2}};
public double knightProbability(int n, int k, int row, int column) {
double[][][] dp = new double[n][n][k + 1];
for (int step = 0; step <= k; step++) {
for (int i = 0; i < n; i++) {
for (int j = 0; j < n; j++) {
if (step == 0) {
dp[i][j][step] = 1;
} else {
for (int[] dir : path) {
int ni = i + dir[0], nj = j + dir[1];
if (ni >= 0 && ni < n && nj >= 0 && nj < n) {
dp[i][j][step] += dp[ni][nj][step - 1] * 0.125;
}
}
}
}
}
}
return dp[row][column][k];
}
}
其运行结果如下:
22 / 22 个通过测试用例
状态:通过
执行用时: 8 ms
内存消耗: 40.2 MB
提交时间:27 分钟前
其时间复杂度为O(k * n ^ 2),空间复杂度为O(k * n ^ 2)。
参考文献
LeetCode官方题解: https://leetcode-cn.com/problems/knight-probability-in-chessboard/solution/qi-shi-zai-qi-pan-shang-de-gai-lu-by-lee-2qhk/