数据结构的学习_4.1 多维数组和运算
4.1 多维数组和运算
4.1.1 数组的顺序存储
数组在各种高级语言中通常有两种不同的顺序存储方式,C语言是按行优先顺序存储的
(1)按行优先顺序存储,即将数组元素按行向量排列,第i+1个行向量紧接在第i个行向量后面。
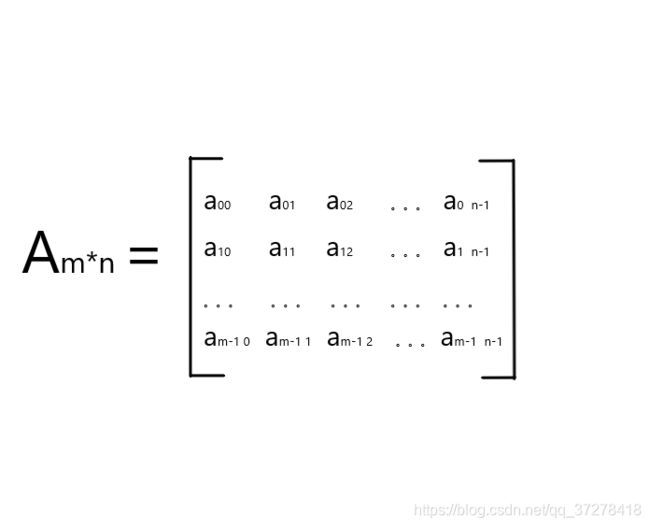
A的m * n 个元素按行优先顺序存储的线性序列为
a 00 , a 01 , . . . , a 0 n − 1 , a 10 , a 11 , . . . , a 1 n − 1 , . . . , a m − 10 , a m − 11 , . . . , a m − 1 n − 1 a_{00},a_{01},...,a_{0n-1},a_{10},a_{11},...,a_{1n-1},...,a_{m-10},a_{m-11},...,a_{m-1n-1} a00,a01,...,a0n−1,a10,a11,...,a1n−1,...,am−10,am−11,...,am−1n−1
(2)按列优先顺序存储,即将数组元素按列向量排列,第j+1个列向量紧接在第j个向量之后
A的m * n 个元素按列优先顺序存储的线性序列为
a 00 , a 10 , . . . , a m − 10 , a 01 , a 11 , . . . , a m − 11 , . . . , a 0 n − 1 , a 1 n − 1 , . . . , a m − 1 n − 1 a_{00},a_{10},...,a_{m-10},a_{01},a_{11},...,a_{m-11},...,a_{0n-1},a_{1n-1},...,a_{m-1n-1} a00,a10,...,am−10,a01,a11,...,am−11,...,a0n−1,a1n−1,...,am−1n−1
如果按这两种方式顺序存储数组,只要知道开始节点的存储地址(即基地址),维数和每维的上、下界,以及每个元素所占用的单元数,就可以将每个数组元素的存储地址表示为其下标的线性函数。
这个二维数组不好表示,插入公式又太丑,a_{m*n}这个就代表a下标m * n 吧
例如:二维数组a_{m*n}按行优先顺序存储在内存中,假设每个元素占d个存储单元,数组a_{i*j}位于第i行、第j列,前面i行共有in个元素,第i行上a_{i * j}前面又有j个元素,因此它的前面一共有in+j个元素,所以在C语言中的数组元素a_{ i * j} 的地址计算函数为:
L O C ( A i j ) = L O C ( a 00 ) + ( i ∗ n + j ) ∗ d LOC(A_{ij})=LOC(a_{00})+(i*n+j)*d LOC(Aij)=LOC(a00)+(i∗n+j)∗d

i * n * p 我的理解是,一层有n * p个,在第i层就是i * ( n * p)个元素,然后j*p+k就是在面上找,加在一起就是元素个数
4.1.2 数组运算举例
例4.1
设计一个算法,实现矩阵A_{m * n}的转置矩阵B_{m * n}
分析:对于一个mn的矩阵A,其转置矩阵是一个nm的矩阵B,而且B[i][j]=A[j][i],0≤i≤n-1,0≤j≤m-1。假设m=5,n=8,其实现算法是
void trsmat (int a[][8] ,int b[][5],int m,int n){
int i,j;
for(j=0;j<m;j++){
for(i=0;i<n;i++){
b[i][j]=a[j][i];
}
}
}
结果举个栗子
A m n A_{mn} Amn
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
B n m B_{nm} Bnm
| 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 |
| 3 | 4 | 5 | 6 | 7 |
| 4 | 5 | 6 | 7 | 8 |
| 5 | 6 | 7 | 8 | 9 |
| 6 | 7 | 8 | 9 | 10 |
| 7 | 8 | 9 | 10 | 11 |
| 8 | 9 | 10 | 11 | 12 |
例4.2
如果矩阵A中存在这样的一个元素A[i][j],满足:A[i][j]是第i行元素中最小值,且又是第j列元素中最大值,则称此元素为该矩阵的一个马鞍点。假设以二维数组存储矩阵A_{m*n},试编写求出矩阵中所有马鞍点的算法
分析:按照题意,先求出每行中的最小值元素,存入数组Min[m]之中再求出每列的最大值元素,存入数组Max[n]之中。若某元素既在Min[i]中又在Max[j]中,则该元素A[i][j]就是马鞍点,找出所有这样元素。因此,实现该题要求算法是:
void MaxMin(int A[4][5] ,int m,int n){
int i,j;
int Max[5],Min[4];
for(i=0;i<m;i++){ //计算每行的最小值元素,存入Min数组中
Min[i]=A[i][0]; //假设第i列第一个元素最小,然后再与后面的元素比较
for(j=1;j<n;j++){
if(A[i][j] < Min[i]){
Min[i]=A[i][j];
}
}
}
for(j=0;j<n;j++){ //计算每列的最大值元素,存入Max数组中
Max[j]=A[0][j]; //假设第j列第一个元素最大,然后再与后面的元素比较
for(i=1;i<m;i++){
if(A[i][j]>Max[j]){
Max[j]=A[i][j];
}
}
}
for(i=0;i<m;i++){ //判断是否为马鞍点
for(j=0;j<n;j++){
if(Min[i]==Max[j]){
printf("(%d,%d)",i,j) //显示马鞍点
}
}
}
}
A m n A_{mn} Amn
| 6 | 5 | 8 | 7 | 9 |
|---|---|---|---|---|
| 7 | 6 | 9 | 11 | 8 |
| 9 | 3 | 6 | 5 | 2 |
| 1 | 4 | 7 | 8 | 3 |