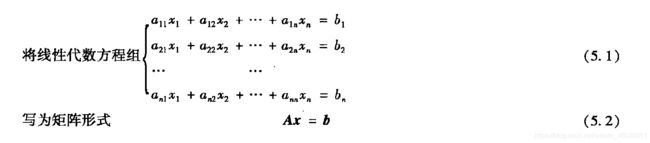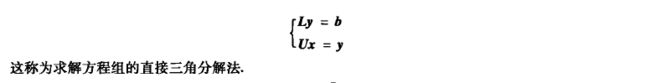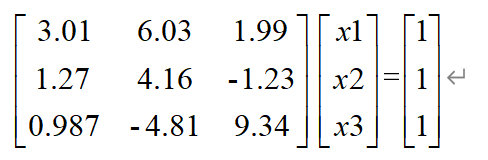数值分析:Python实现列主元高斯消去法与LU分解法求解线性方程组
Python实现列主元高斯消去法与LU分解法
数值分析:Python实现列主元高斯消去法与LU分解法求解线性方程组
一、矩阵形式的线性代数方程组
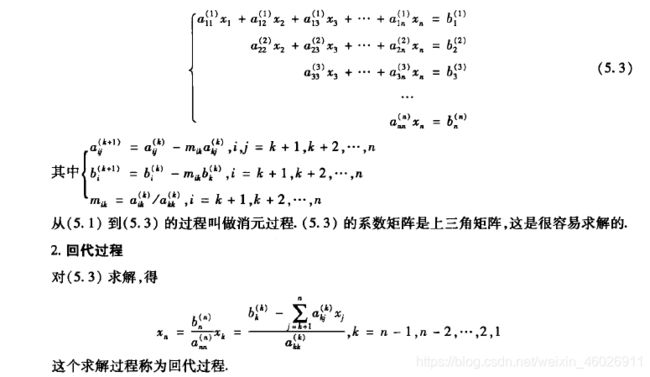
二、高斯消去法
三、高斯列主元消去法
四、矩阵三角分解法(LU分解)
题目:编写列主元高斯消去法与LU分解法解线性方程组Ax=b。
import math
import numpy as np
#目的:熟悉列主元消去法,以及三角分解法等直接求解线性方程组的算法
#列主元消元法
def CME(a,b,x):
isdet0 = 0
m, n = a.shape #矩阵a的行数和列数
# j表示列
for k in range(n - 1): # k表示第一层循环,(0,n-1)行
#在每次计算前,找到最大主元,进行换行
ans = np.fabs(a[k][k])
ik = k
for i in range(k+1, n):
if ans < np.fabs(a[i][k]): # fabs是绝对值,将a中绝
对值最大的找出来
ik = i
ans = np.fabs(a[i][k])
if np.fabs(ans) < 1e-10:
isdet0 = 1
break
if ik != k :
for i in range(k,m):
temp = a[k][i]
a[k][i] = a[ik][i]
a[ik][i] = temp
temp = b[k]
b[k] = b[ik]
b[ik] = temp
for i in range(k + 1, n): # i表示第二层循环,(k+1,n)行,
计算该行消元的系数
temp = a[i][k] / a[k][k] #计算
for j in range(k,m): # j表示列,对每一列进行运算
a[i][j] = a[i][j] - temp * a[k][j]
b[i] = b[i] - temp * b[k]
# 回代求出方程解
if np.fabs(a[n-1][n-1]) < 1e-10 :
isdet0 = 1
if isdet0 == 0:
# x = np.zeros(n)
x[n - 1] = b[n - 1] / a[n - 1][n - 1] #先算最后一位的x解
for i in range(n - 2, -1, -1): #依次回代倒着算每一个解
temp = 0
for j in range(n - 1, i,-1):
temp = temp + a[i][j]*x[j]
x[i] = (b[i]-temp) / a[i][i]
for i in range(n):
print("x" + str(i + 1) + " = ", x[i])
print("x" " = ", x)
if __name__ == '__main__': #当模块被直接运行时,以下代码块将被运行,当模块是被导入时,代码块不被运行。
a = np.array([[3.01, 6.03, 1.99], [1.27, 4.16, -1.23], [0.987, -4.81, 9.34]])
b = np.array([1.0, 1.0, 1.0])
m,n = a.shape
x = np.zeros(n)
B = np.zeros((n, n))
for i in range(n):
for j in range(n):
B[i][j] = a[i][j]
CME(a,b,x)
#验证
for i in range(0, n):
temp = 0
for j in range(0, n):
temp = temp + B[i][j] * x[j]
print("%f ", temp)
if __name__ == '__main__':
main()
LU分解法代码实现:
import math
import numpy as np
#目的:熟悉列主元消去法,以及三角分解法等直接求解线性方程组的算法
#列主元消元法
def CME(a,b,x):
isdet0 = 0
m, n = a.shape #矩阵a的行数和列数
# j表示列
for k in range(n - 1): # k表示第一层循环,(0,n-1)行
#在每次计算前,找到最大主元,进行换行
ans = np.fabs(a[k][k])
ik = k
for i in range(k+1, n):
if ans < np.fabs(a[i][k]): # fabs是绝对值,将a中绝对值最大的找出来
ik = i
ans = np.fabs(a[i][k])
if np.fabs(ans) < 1e-10:
isdet0 = 1
break
if ik != k :
for i in range(k,m):
temp = a[k][i]
a[k][i] = a[ik][i]
a[ik][i] = temp
temp = b[k]
b[k] = b[ik]
b[ik] = temp
for i in range(k + 1, n): # i表示第二层循环,(k+1,n)行,计算该行消元的系数
temp = a[i][k] / a[k][k] #计算
for j in range(k,m): # j表示列,对每一列进行运算
a[i][j] = a[i][j] - temp * a[k][j]
b[i] = b[i] - temp * b[k]
# 回代求出方程解
if np.fabs(a[n-1][n-1]) < 1e-10 :
isdet0 = 1
if isdet0 == 0:
# x = np.zeros(n)
x[n - 1] = b[n - 1] / a[n - 1][n - 1] #先算最后一位的x解
for i in range(n - 2, -1, -1): #依次回代倒着算每一个解
temp = 0
for j in range(n - 1, i,-1):
temp = temp + a[i][j]*x[j]
x[i] = (b[i]-temp) / a[i][i]
for i in range(n):
print("x" + str(i + 1) + " = ", x[i])
print("x" " = ", x)
#三角消元法
def LU(a,b,x):
m, n = a.shape # 矩阵a的行数和列数
y = np.array([0.0, 0.0, 0.0])
for j in range(1,n):# L的第0列
a[j][0] = a[j][0] / a[0][0]
for i in range(1,n-1):# 求U的第i行 L的第i行
for j in range(i,n):#求U的第i行的第j个元素
sum = 0.0 #求和
for s in range(0,i):
sum = sum +a[i][s] * a[s][j]
a[i][j] = a[i][j] - sum
#求L的第i列的第j个元素 在j行i列
for j in range(i+1,n):
sum = 0.0
for s in range(0,i):
sum = sum + a[j][s] * a[s][i]
a[j][i] = ( a[j][i] - sum ) / a[i][i]
#求U[n-1][n-1]
sum = 0.0 #求和
for s in range(0,n-1):
sum = sum + a[n-1][s] * a[s][n-1]
a[n-1][n-1] = a[n-1][n-1] - sum
y[0] = b[0]
for i in range(1,n):
sum = 0.0
for j in range(0,i):
sum = sum + a[i][j] * y[j]
y[i] = b[i] - sum
x[n-1] = y[n-1] / a[n-1][n-1]
for i in range(n-2,-1,-1):#求x[i]
sum = 0.0
for j in range(n-1,i,-1):
sum = sum + a[i][j] * x[j]
x[i] = ( y[i] - sum ) / a[i][i]
for i in range(n):
print("x" + str(i + 1) + " = ", x[i])
print("x" " = ", x)
if __name__ == '__main__': #当模块被直接运行时,以下代码块将被运行,当模块是被导入时,代码块不被运行。
a = np.array([[3.01, 6.03, 1.99], [1.27, 4.16, -1.23], [0.987, -4.81, 9.34]])
b = np.array([1.0, 1.0, 1.0])
m,n = a.shape
x = np.zeros(n)
B = np.zeros((n, n))
for i in range(n):
for j in range(n):
B[i][j] = a[i][j]
# CME(a,b,x)
LU(a,b,x)
#验证
for i in range(0, n):
temp = 0
for j in range(0, n):
temp = temp + B[i][j] * x[j]
print("%f ", temp)