2020_10_17 每日一题 N皇后II
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上,并且使皇后彼此之间不能相互攻击。
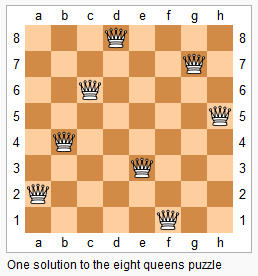
上图为 8 皇后问题的一种解法。
给定一个整数 n,返回 n 皇后不同的解决方案的数量。
示例:
输入: 4 输出: 2 解释: 4 皇后问题存在如下两个不同的解法。
[
[".Q…", // 解法 1
“…Q”,
“Q…”,
“…Q.”],["…Q.", // 解法 2
“Q…”,
“…Q”,
“.Q…”] ]来源:力扣(LeetCode) 链接:https://leetcode-cn.com/problems/n-queens-ii
著作权归领扣网络所有。商业转载请联系官方授权,非商业转载请注明出处。
总感觉昨天每日一题才出过N皇后问题:
N皇后
由于只用求方案数,其实是更省事了,连每行的情况都不用记录了:
class Solution {
boolean[] cols, ur, ul;
int ret;
int N;
int add;
boolean isSet(int row, int col) {
return ul[row - col + N - 1] || ur[row + col] || cols[col];
}
void set(int row, int col, boolean set) {
ul[row - col + N - 1] = set;
ur[row + col] = set;
cols[col] = set;
}
void rec(int row) {
if(row == N) {
ret += add;
return;
}
//System.out.println(row);
for(int i = 0; i < N; ++i) {
if(!isSet(row, i)) {
set(row, i, true);
rec(row + 1);
set(row, i, false);
}
}
}
public int totalNQueens(int n) {
if(n <= 1)
return n;
N = n;
cols = new boolean[n];
ur = new boolean[2 * n + 1];
ul = new boolean[2 * n + 1];
ret = 0;
add = 2;
for(int i = 0; i < n / 2; ++i){
set(0, i, true);
rec(1);
set(0, i, false);
}
if(n % 2 == 1) {
add = 1;
set(0, n / 2, true);
rec(1);
}
return ret;
}
}