LeetCode:二叉树刷题(篇章二)
往期回顾
- LeetCode:二叉树刷题(篇章一)
文章目录
- 往期回顾
- 前言
- 一、本期攻克题目
- 二、二叉树解题框架回顾
- 三、题解
-
- 3.1 翻转二叉树
- 3.2 填充每个节点的下一个右侧节点指针
- 3.3 二叉树展开为链表
- 3.4 最大二叉树
- 3.5 从前序与中序遍历序列构造二叉树
- 3.6 从中序与后序遍历序列构造二叉树
- 3.7 寻找重复的子树
- 总结
前言
本篇是跟着labuladong算法小抄刷题《二叉树》的第二个章节,发布博客的目的是为了加深记忆,以熟练算法框架为目的,解题思路并非原创。 参考资料已在文中多个位置进行引用,整理不易,多多支持吧。
一、本期攻克题目
- LeetCode226:翻转二叉树
- LeetCode116:填充每个节点的下一个右侧节点指针
- LeetCode114:二叉树展开为链表
- LeetCode654:最大二叉树
- LeetCode105:从前序与中序遍历序列构造二叉树
- LeetCode106:从中序与后序遍历序列构造二叉树
- LeetCode652:寻找重复的子树
二、二叉树解题框架回顾
解决二叉树相关的问题离不开对树的各种遍历,因此掌握了二叉树的前、中、后序方法,再去思考根节点(root)、子节点干了什么,应该放在前、中、后序的哪个位置【注意结合递归思想,但不要陷入递归的细节里面】,便可解题。除此之外,还需要考虑借助辅助函数进行解题。
注意: 二叉树题目的一个难点就是,如何把题目的要求细化成每个节点需要做的事情。
/* 二叉树遍历框架 */
void traverse(TreeNode* root) {
// 前序遍历
traverse(root->left)
// 中序遍历
traverse(root->right)
// 后序遍历
}
三、题解
3.1 翻转二叉树
题目要求:
翻转一棵二叉树。
通过对输入输出的观察,可以发现,root不变,然后我们只要把二叉树上的每一个节点的左右子节点进行交换,最后的结果就是完全翻转之后的二叉树。 代码见下。
C++实现:
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if (root==nullptr) {
return nullptr;
}
TreeNode* tmp;
tmp = root->left;
root->left = root->right;
root->right = tmp;
invertTree(root->left);
invertTree(root->right);
return root;
}
};
Python实现:
class Solution:
def invertTree(self, root: TreeNode) -> TreeNode:
if not root:
return root
root.left, root.right = root.right, root.left
self.invertTree(root.left)
self.invertTree(root.right)
return root
3.2 填充每个节点的下一个右侧节点指针
题目要求:
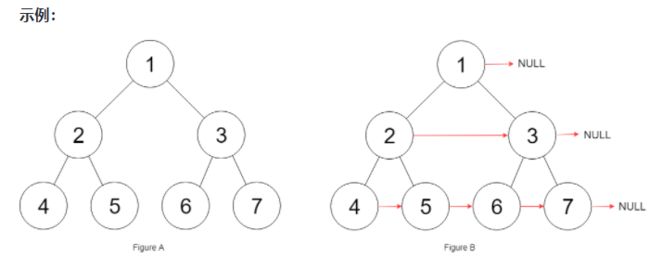
给定一个 完美二叉树 ,其所有叶子节点都在同一层,每个父节点都有两个子节点。填充它的每个 next 指针,让这个指针指向其下一个右侧节点。如果找不到下一个右侧节点,则将 next 指针设置为 NULL。初始状态下,所有 next 指针都被设置为 NULL。
示例:
输入:root = [1,2,3,4,5,6,7]
输出:[1,#,2,3,#,4,5,6,7,#]
解释:给定二叉树如图 A 所示,你的函数应该填充它的每个 next 指针,以指向其下一个右侧节点,如下图所示。序列化的输出按层序遍历排列,同一层节点由 next 指针连接,’#’ 标志着每一层的结束。
解题思路:
根据题目,我们可以很容易的想到,将每个二叉树的左节点和右节点连接起来即可,但是会出现一个问题就是左子树的右孩子节点与右子树的左孩子节点是没有办法被连接的。因此,可以想到只依赖一个节点的话,肯定是没办法连接「跨父节点」的两个相邻节点的。那么,我们的做法就是增加函数参数,一个节点做不到,我们就给他安排两个节点,「将每一层二叉树节点连接起来」可以细化成「将每两个相邻节点都连接起来」。 代码见下。
C++实现:
class Solution {
public:
void connectTwoNode(Node* node1, Node* node2) {
if (node1 == NULL || node2 == NULL) {
return ;
}
/**** 前序遍历位置 ****/
// 将传入的两个节点连接
node1->next = node2;
// 连接相同父节点的两个子节点
connectTwoNode(node1->left, node1->right);
connectTwoNode(node2->left, node2->right);
// 连接跨越父节点的两个子节点
connectTwoNode(node1->right, node2->left);
}
Node* connect(Node* root) {
if (root == NULL) {
return NULL;
}
connectTwoNode(root->left, root->right);
return root;
}
};
Python实现:
class Solution:
def connectTwoNode(self, node1: 'Optional[Node]', node2: 'Optional[Node]') -> 'Optional[Node]':
if not node1 or not node2:
return None
node1.next = node2
# 连接相同父节点的两个子节点
self.connectTwoNode(node1.left, node1.right)
self.connectTwoNode(node2.left, node2.right)
# 连接跨越父节点的两个子节点
self.connectTwoNode(node1.right, node2.left)
def connect(self, root: 'Optional[Node]') -> 'Optional[Node]':
if not root:
return None
self.connectTwoNode(root.left, root.right)
return root
3.3 二叉树展开为链表
题目要求:
给你二叉树的根结点 root ,请你将它展开为一个单链表:展开后的单链表应该同样使用 TreeNode ,其中 right 子指针指向链表中下一个结点,而左子指针始终为 null 。展开后的单链表应该与二叉树 先序遍历 顺序相同。
示例:
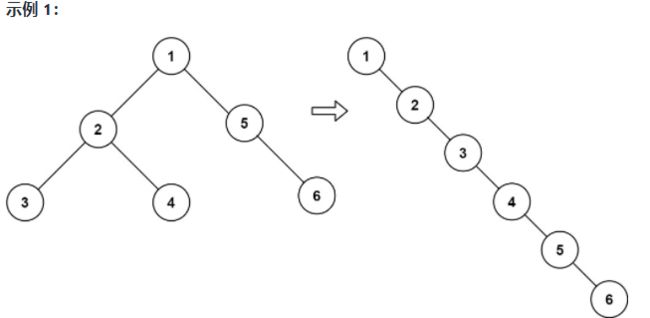
输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
解题思路:
本题较难理解,写下原作大大的思路,注意:不要陷入递归的细节里面,【作为小白的我,真的好难理解通T_T】。
给 flatten 函数输入一个节点 root,那么以 root 为根的二叉树就会被拉平为一条链表。我们再梳理一下,如何按题目要求把一棵树拉平成一条链表?很简单,以下流程:
1. 将 root 的左子树和右子树拉平;
2. 将 root 的右子树接到左子树下方,然后将整个左子树作为右子树;这就是递归的魅力,你说 flatten 函数是怎么把左右子树拉平的?说不清楚,但是只要知道 flatten 的定义如此,相信这个定义,让 root 做它该做的事情,然后 flatten 函数就会按照定义工作。另外注意递归框架是后序遍历,因为我们要先拉平左右子树才能进行后续操作。
C++实现:
class Solution {
public:
void flatten(TreeNode* root) {
// base case
if (root == nullptr) {
return ;
}
flatten(root->left);
flatten(root->right);
/**** 后序遍历位置 ****/
// 1、左右子树已经被拉平成一条链表
TreeNode* left = root->left;
TreeNode* right = root->right;
// 2、将左子树作为右子树
root->left = nullptr;
root->right = left;
// 3、将原先的右子树接到当前右子树的末端
TreeNode* p = root;
while (p->right != nullptr) {
p = p->right;
}
p->right = right;
}
};
Python实现:
class Solution:
def flatten(self, root: TreeNode) -> None:
"""
Do not return anything, modify root in-place instead.
"""
if not root:
return;
# 先递归拉平左右子树
self.flatten(root.left)
self.flatten(root.right)
# /****后序遍历位置****/
# 1、左右子树已经被拉平成一条链表
left=TreeNode(None)
left = root.left
right=TreeNode(None)
right= root.right
# 2、将左子树作为右子树
root.left = None
root.right = left
# 3、将原先的右子树接到当前右子树的末端
p = TreeNode(None)
p = root
while p.right != None:
p = p.right
p.right = right
3.4 最大二叉树
题目要求:
给定一个不含重复元素的整数数组 nums 。一个以此数组直接递归构建的 最大二叉树 定义如下:
- 二叉树的根是数组 nums 中的最大元素;
- 左子树是通过数组中 最大值左边部分 递归构造出的最大二叉树;
- 右子树是通过数组中 最大值右边部分 递归构造出的最大二叉树;
- 返回有给定数组 nums 构建的 最大二叉树 。
示例:
输入:nums = [3,2,1,6,0,5]
输出:[6,3,5,null,2,0,null,null,1]
解释:递归调用如下所示:
- [3,2,1,6,0,5] 中的最大值是 6 ,左边部分是 [3,2,1] ,右边部分是 [0,5] 。
- [3,2,1] 中的最大值是 3 ,左边部分是 [] ,右边部分是 [2,1] 。
- 空数组,无子节点。
- [2,1] 中的最大值是 2 ,左边部分是 [] ,右边部分是 [1] 。
- 空数组,无子节点。
- 只有一个元素,所以子节点是一个值为 1 的节点。
- [0,5] 中的最大值是 5 ,左边部分是 [0] ,右边部分是 [] 。
- 只有一个元素,所以子节点是一个值为 0 的节点。
- 空数组,无子节点。
解题思路:
先明确根节点做什么?对于构造二叉树的问题,根节点要做的就是把想办法把自己构造出来。 具体做法:遍历数组把找到最大值 maxVal,把根节点 root 做出来,然后对 maxVal 左边的数组和右边的数组进行递归调用,作为 root 的左右子树。 C++的代码参考的LeetCode官方题解,labuladong算法小抄的解法是Java写的,一直没有成功改成C++的代码,它的解题思路与官方大致是相同的。
C++实现:
class Solution {
private:
// 在左闭右开区间[left, right),构造二叉树
TreeNode* traversal(vector<int>& nums, int left, int right) {
if (left >= right) return nullptr;
// 分割点下表:maxValueIndex
int maxValueIndex = left;
for (int i = left + 1; i < right; ++i) {
if (nums[i] > nums[maxValueIndex]) maxValueIndex = i;
}
TreeNode* root = new TreeNode(nums[maxValueIndex]);
// 左闭右开:[left, maxValueIndex)
root->left = traversal(nums, left, maxValueIndex);
// 左闭右开:[maxValueIndex + 1, right)
root->right = traversal(nums, maxValueIndex + 1, right);
return root;
}
public:
TreeNode* constructMaximumBinaryTree(vector<int>& nums) {
return traversal(nums, 0, nums.size());
}
};
Python实现:
class Solution:
def build(self, nums: List[int], left, right):
if (left >= right):
return None
maxValueIndex=left
for i in range(left+1, right):
if (nums[i] > nums[maxValueIndex]):
maxValueIndex = i
root = TreeNode(nums[maxValueIndex])
root.left = self.build(nums, left, maxValueIndex)
root.right = self.build(nums, maxValueIndex+1, right)
return root
def constructMaximumBinaryTree(self, nums: List[int]) -> TreeNode:
return self.build(nums, 0, len(nums))
3.5 从前序与中序遍历序列构造二叉树
题目要求:
给定一棵树的前序遍历 preorder与中序遍历 inorder。请构造二叉树并返回其根节点。
示例:
Input: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
Output: [3,9,20,null,null,15,7]
解题思路:
根据先序和中序的性质,确定root的位置,然后根据下图去确定,左右子树的范围,然后递归的构建左右子树。
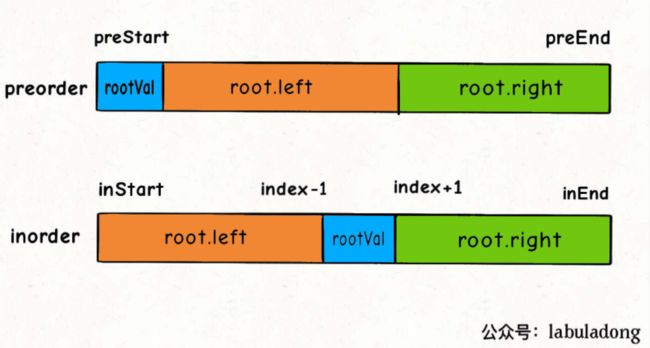
C++实现:
class Solution {
public:
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
return build(preorder, 0, preorder.size() -1 , inorder, 0, inorder.size() - 1);
}
TreeNode* build(vector<int>& preorder, int preStart, int preEnd, vector<int>& inorder, int inStart, int inEnd) {
if(preStart > preEnd) {
return nullptr;
}
// root 节点对应的值就是前序遍历数组的第一个元素
int rootVal = preorder[preStart];
// rootVal 在中序遍历数组中的索引
int index =0;
for(int i=inStart; i<=inEnd; i++) {
if(inorder[i] == rootVal) {
index = i;
break;
}
}
int leftSize = index - inStart;
//先构造出当前根节点
TreeNode* root = new TreeNode(rootVal);
//递归构造左右子树
root->left = build(preorder, preStart + 1, preStart + leftSize,
inorder, inStart, index - 1);
root->right = build(preorder, preStart + leftSize + 1, preEnd,
inorder, index + 1, inEnd);
return root;
}
};
Python实现:
class Solution:
def build(self, preorder: List[int], preStart, preEnd, inorder: List[int], inStart, inEnd) -> TreeNode:
if preStart > preEnd:
return None;
# 定位根节点
rootVal = preorder[preStart]
index=0
for i in range(len(inorder)):
if inorder[i] == rootVal:
index = i
break
leftSize = index - inStart
# 定义根节点
root = TreeNode(rootVal)
root.left = self.build(preorder, preStart + 1, preStart + leftSize, inorder, inStart, index - 1)
root.right = self.build(preorder, preStart + leftSize + 1, preEnd, inorder, index + 1, inEnd)
return root
def buildTree(self, preorder: List[int], inorder: List[int]) -> TreeNode:
return self.build(preorder, 0, len(preorder) - 1, inorder, 0, len(inorder) - 1)
3.6 从中序与后序遍历序列构造二叉树
题目要求:
根据一棵树的中序遍历与后序遍历构造二叉树。
示例:
中序遍历 inorder = [9,3,15,20,7]
后序遍历 postorder = [9,15,7,20,3]
返回如下图:
解题思路:
此题的解法跟上一题是一致的,无外乎左右子树的区间零界点更换了,区间如下图所示。
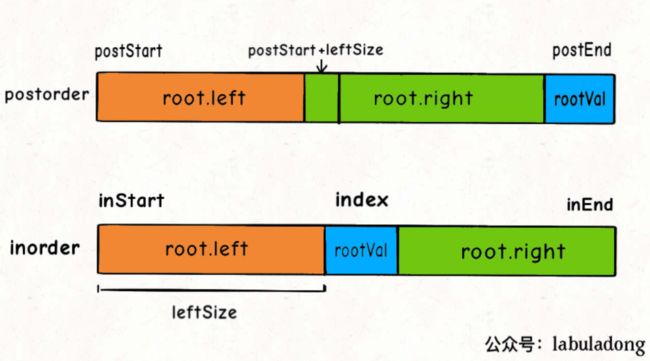
C++实现:
class Solution {
public:
TreeNode* buildTree(vector<int>& inorder, vector<int>& postorder) {
return build(inorder, 0, inorder.size() - 1,
postorder, 0, postorder.size() - 1);
}
/*
定义:
中序遍历数组为 inorder[inStart..inEnd],
后序遍历数组为 postorder[postStart..postEnd],
构造这个二叉树并返回该二叉树的根节点
*/
TreeNode* build(vector<int>& inorder, int inStart, int inEnd,
vector<int>& postorder, int postStart, int postEnd) {
if (inStart > inEnd) {
return nullptr;
}
// root 节点对应的值就是后序遍历数组的最后一个元素
int rootVal = postorder[postEnd];
// rootVal 在中序遍历数组中的索引
int index = 0;
for (int i = inStart; i <= inEnd; i++) {
if (inorder[i] == rootVal) {
index = i;
break;
}
}
// 左子树的节点个数
int leftSize = index - inStart;
TreeNode* root = new TreeNode(rootVal);
// 递归构造左右子树
root->left = build(inorder, inStart, index - 1,
postorder, postStart, postStart + leftSize - 1);
root->right = build(inorder, index + 1, inEnd,
postorder, postStart + leftSize, postEnd - 1);
return root;
}
};
Python实现:
class Solution:
def build(self, inorder: List[int], inStart, inEnd, postorder: List[int], postStart, postEnd, ) -> TreeNode:
if inStart > inEnd:
return None
#定位根的位置
rootVal = postorder[postEnd]
#遍历中序数组
index = 0
for i in range(len(inorder)):
if inorder[i] == rootVal:
index = i
break
leftSize = index - inStart
# 定义根节点
root = TreeNode(rootVal)
root.left = self.build(inorder, inStart, index - 1, postorder, postStart, postStart+leftSize -1)
root.right = self.build(inorder, index + 1, inEnd, postorder, postStart+leftSize, postEnd -1)
return root
def buildTree(self, inorder: List[int], postorder: List[int]) -> TreeNode:
return self.build(inorder, 0, len(inorder)-1, postorder, 0, len(postorder)-1)
3.7 寻找重复的子树
题目要求:
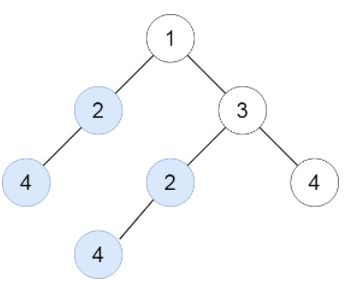
给定一棵二叉树 root,返回所有重复的子树。对于同一类的重复子树,你只需要返回其中任意一棵的根结点即可。如果两棵树具有相同的结构和相同的结点值,则它们是重复的。
示例:
解题思路:
C++实现:
在这里插入代码片
Python实现:
在这里插入代码片
总结
强烈推荐labuladong算法小抄,之前觉得刷题太难了,跟着练习,感觉二叉树问题并没有那么可怕了,但还是不够熟练,继续加油吧,刷起来。