Leetcode 刷题笔记：字符串篇

//结束了忙碌的期末，终于有了一个月的冬假，赶紧利用这段时间集中精力把Leetcode刷起来！

1.Leetcode344 反转字符串（题解）

难度：⭐️

这道题目算是比较基础也是很简单的一道题目了，用双指针的方法可以轻松解决。时间复杂度O(N)，空间复杂度O(1)。具体代码。

在反转链表中，使用了双指针的方法。

那么反转字符串依然是使用双指针的方法，只不过对于字符串的反转，其实要比链表简单一些。

因为字符串也是一种数组，所以元素在内存中是连续分布，这就决定了反转链表和反转字符串方式上还是有所差异的。

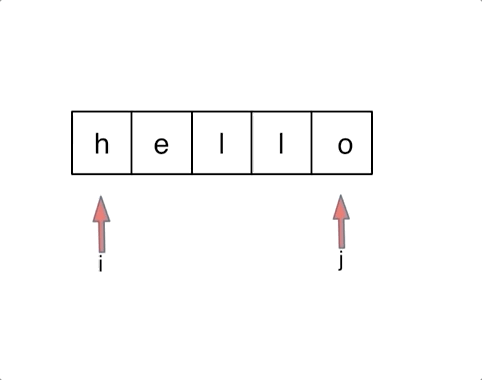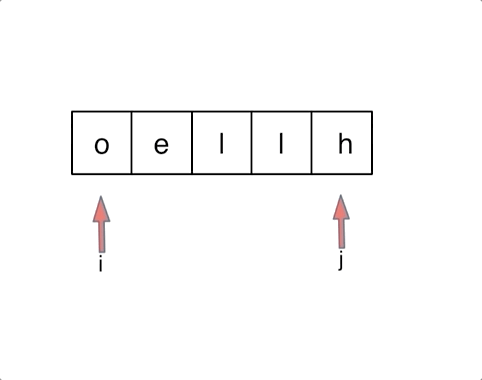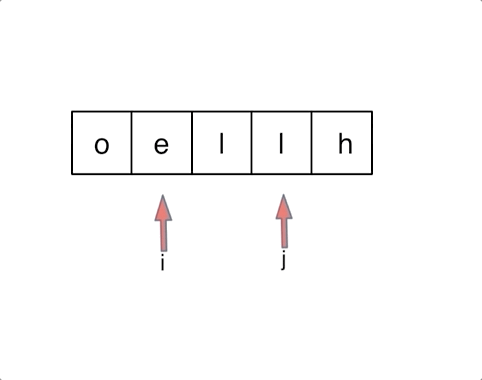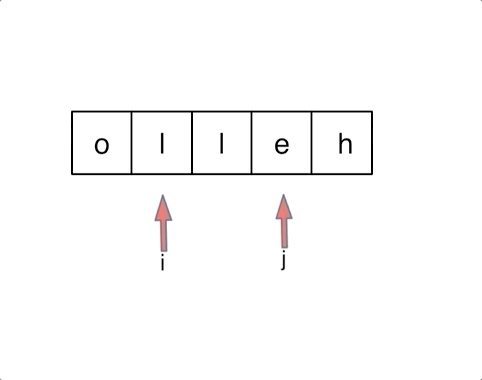
对于字符串，我们定义两个指针（也可以说是索引下标），一个从字符串前面，一个从字符串后面，两个指针同时向中间移动，并交换元素。

以字符串hello为例，过程如下：

 至于交换swap的实现，有三种方法：交换指针地址（本题不适用，因为要迭代）、交换数值（常用）、位运算。这里简单说一下位运算的实现：

Template void swap(T& x, T& y){

X^=y;

y^=x;

x^=y;

}

这里^是位异或运算符，A^A=0, 0^B=B。

最后提一下，本题仅需一行代码就能解决，即使用库函数reverse(s.begin(), s.end())；然而这样做便失去了题目的精髓。本题就是让你自己实现一个reverse方法。

2.Leetcode541 反转字符串II（题解）

难度：⭐️⭐️

这道题算是在上一题的基础上，加了一下判断和操作条件，需要以2k为区间，反转前k区间的字符串。一共需要O(n/2k)次循环，每次循环时完成反转需要O(k)，因此总时间复杂度为O(n/2k)*O(k)=O(n)，空间复杂度为O(1)。

思路1:先定义一个变量来存储剩余元素个数，然后每次循环递减2k，同时对这个区间的前k个元素反转，最后循环结束后，判断一下剩余元素个数，如果小于k，只反转剩下的部分，反之反转前k个元素。具体代码。

思路2：直接以2k区间大小来循环遍历，然后在循环函数体内判断2k区间实际包含的元素数量，如果小于k，则只反转开始位置到结束位置的字符，否则反转整个k区间。具体代码。（这样写虽然不用在循环结束后额外判断，但循环内需要多判断一次，相比思路1有利有弊）

官方题解的代码更加精妙，直接用reverse(s.begin()+i, s.begin()+ min(i+k, size))将两种判断情况合二为一。

3.剑指Offer05 替换空格（题解）

难度：⭐️⭐️

这道题有两个思路。

第一个是正向遍历+正向替换，在正向遍历的过程中，每遇到一个空格，就resize字符串长度+2，并且从后往前，将空格位置之后的每个字符后移2位，最后再替换空格位置及其后两个位置的值为“%20”。时间复杂度O(n2)，空间复杂度O(1)。具体代码。

也可以空间换时间，通过新开辟一个字符串，遍历并将s中每个字符拷贝到新的字符串中，遇到空格则拷贝替换值。时间复杂度O(n)，空间复杂度O(n)。具体代码。

第二个是正向遍历+反向替换，首先遍历一遍整个字符串s，统计空格个数space_num，然后resize字符串为s.size()+space_num*2，最后从后往前将每个字符后移2*space_num位，如果遇到空格则后移2*(space_num-1)位，并将后面的3位替换为”%20”，同时将space_num—，直到为0结束。时间复杂度O(n)，空间复杂度O(1)。具体代码。

题解在替换时给到了双指针法，但其实用单指针+偏移量也可以实现。

这里也给大家拓展一下字符串和数组有什么差别：

在C语言中，把一个字符串存入一个数组时，也把结束符 '\0'存入数组，并以此作为该字符串是否结束的标志。

例如这段代码：

char a[5] = "asd";
for (int i = 0; a[i] != '\0'; i++) {
}

在C++中，提供一个string类，string类会提供 size接口，可以用来判断string类字符串是否结束，就不用'\0'来判断是否结束。

例如这段代码:

string a = "asd";
for (int i = 0; i < a.size(); i++) {
}

那么vector< char > 和 string 又有什么区别呢？

其实在基本操作上没有区别，但是 string提供更多的字符串处理的相关接口，例如string 重载了+，而vector却没有。

所以想处理字符串，我们还是会定义一个string类型。​​​​​​​

4.Leetcode151 翻转字符串里的单词（题解）

难度：⭐️⭐️⭐️

这道题还是稍微有一点难度的，比较容易想到的解法，是借助辅助空间来存放翻转顺序后的单词。

解法1: 正向遍历+裁剪单词，建立一个临时字符串s，每当遍历到非空格字符时，将之后到每个字符存入s中，直到原字符串的末尾，或者遇到新的空格为止，然后将s压入vector/duque的末尾，最后依次从末端取出，便得到了翻转顺序后的单词。裁剪的过程也可以用的库函数strtok来实现。具体代码。时间复杂度O(n)，空间复杂度O(n)。

解法2: 反向遍历+裁剪单词，利用双指针的思想，用一个指针r从后往前遍历，指向第一个有效字符，然后另一个指针l继续从这个位置向前遍历，当遇到空格，或者字符串开头位置时停止，然后将l+1（遇到空格）或l（字符串开头）到r到这段字符，保存到结果数组s中。这种方式直接实现了翻转字符，无需通过vector/deque的push/pop来实现翻转。具体代码。时间复杂度O(n)，空间复杂度O(n)。

解法3:正向遍历+裁剪空格+翻转整个字符+翻转局部单词，通过后两个步骤的两次翻转，可以实现题目要求的结果。通过这种方式可以实现O(1)的空间复杂度，时间复杂度仍为O(n)。具体代码。另外一个优化版本，在正向遍历时，将裁减空格和翻转局部单词的操作合二为一。具体代码​​​​​​​。

5.剑指Offer58II 左旋转字符串（题解）

难度：⭐️⭐️

这道题可以看作上一道题的浓缩版。只需要将两个相连的"单词"进行翻转。

解法1: 先用一个临时字符串tmp保存长度为n的左旋转字符串，然后从第n+1个字符开始，将每个字符左移n位，最后将之前临时字符串的内容，依次写入到从s.size()-1-(n-1)=s.size()-n开始的n个位置。时间复杂度O(n)，空降复杂度O(c)，其中c为需要左旋转的字符串长度。具体代码。

解法2:使用上一题的解法三的后两步，翻转局部字符串+翻转整个字符串，首先分别将第1到第n个字符翻转，然后将n+1到最后一个字符翻转，最后将整个字符串翻转即可。时间复杂度O(n)，空间复杂度O(1)。具体代码​​​​​​​。

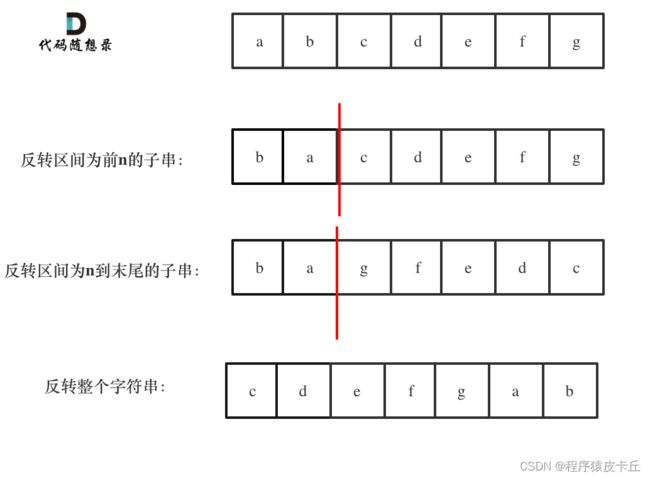
具体步骤为：

1. 反转区间为前n的子串
2. 反转区间为n到末尾的子串
3. 反转整个字符串

最后就可以达到左旋n的目的，而不用定义新的字符串，完全在本串上操作。

例如 ：示例1中 输入：字符串abcdefg，n=2

如图：

 最终得到左旋2个单元的字符串：cdefgab

思路明确之后，那么代码实现就很简单了。

6.Leeetcode28 实现strStr()（题解）

难度：⭐️⭐️⭐️⭐️⭐️

这道题居然只是中等难度。。？（更新：现在居然变成简单了？？？）光把KMP算法吃透，我就啃了整整三天T T。。给个五星难度以示尊重。。

如果单纯用暴力解法，具体代码。时间复杂度O(mn)，空间复杂度O(1)。

而如果用KMP算法。时间复杂度为O(m+n)，空间复杂度为O(m)。

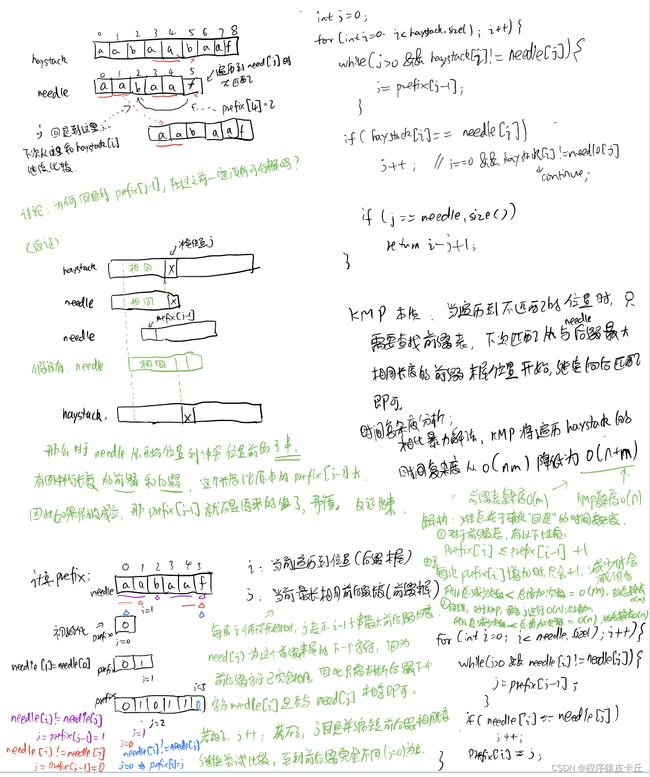
这道题目分为两个大的步骤：建立前缀表、通过KMP算法用前缀表查找相同字符串。

建立前缀表：用j表示当前子串的最大相同前后缀长度，初始化prefix[0]，j=0，用i开始遍历needle，当冲突(needle[i]!=needle[j])时，用while循环不断回退j。如果不冲突，则j++。最后记录结果prefix[i]=j并继续循环遍历。

用前缀表查找相同字符串：用i遍历haystack，用j遍历needle，当冲突时，用while循环不断回退j到prefix[j-1]，继续判断新的压缩长度后的前缀的下一个字符是否与i当前的字符冲突。如果不冲突，则j++，然后进行下一次循环(i++)，继续遍历haystack的下一个字符，判断是否与j冲突。直到j==needle.size()时，返回结果，即haystack中与needle相同字符串的起始位置。

题解具体实现代码。

此外，在用前缀表查找字符串的过程中，我自己还使用另外一种滑动窗口的解法。让i指向haystack中窗口的起始位置，j控制窗口的大小，i+j为滑动窗口的末尾位置。这样其实就有两个窗口了，haystack[i:i+j-1]和needle[0:j-1]。每次遇到冲突（haystack[i+j]!=needle[j]）时，回退j=prefix[j-1]，同时调整i=i+j-prefix[j-1]。不过这样需要同时维护两个变量i,j来调整窗口的大小，相比题解只用j指向haystack末尾位置的解法稍显繁琐。具体实现代码（详细注释版、精简注释版、补充注释版）

具体细节步骤可参考题解文章，我自己也画了一张图进行总结。

除了基本代码和思路外，还针对了一些细节问题进行分析讨论，比如在冲突时j回退到prefix[j-1]，为什么在这之前不可能有答案。以及为什么时间复杂度是O(m+n)。

//多说一句，如果在代码中加入了if(needle.size()>haystack.size()) return -1;的判断条件，时间复杂度可以直接简写为O(n)。

这道题力扣官方题解直接把KMP推理证明了一番。。不过我感觉自己已经理解的差不多了，证明以后有时间再看吧。。

补充：这道题目也可以用滚动哈希来做，时间复杂度O(m+n)即O(n)，空间复杂度O(1)。具体代码。

7.Leetcode459 重复的子字符串（题解​​​​​​​）

难度：⭐️⭐️⭐️

这道题算是KMP算法的一个应用，即使已经搞懂了这个算法，想要触类旁通还是有些困难的，重点是要发现并摸清题目的规律。一个很好的尝试方法就是举例子。

先说暴力解法，第一层for循环i遍历重复子串的长度（可通过是否能被size整除，以及iO(n2)，空间复杂度O(1)。

接下来就要考虑是否能用KMP实现更高效的解法了。那么就需要找规律。尝试写出几个例子的前缀表之后，发现了规律所在。

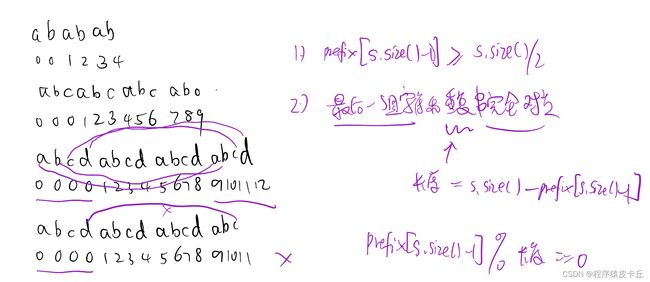
可以看到，从第二个重复串开始，前缀prefix的值会逐一累加，因此要满足重复条件，那么重复子串的长度就不能超过size的一半，那么prefix的值就应该大于等于size的一半。其次，还需要保证最后一次也是完整的子串重复，那么只需要计算所有重复字符的数量prefix[size-1]能否被子串的长度size-prefix[size-1]整除就可以了。具体代码。时间复杂度O(n)，空间复杂度O(n)。

题解还提到了一个移动匹配的解法。就是说将两个s拼在一起，掐头去尾一个字符后，如果中间还能找到s，说明s是由重复子串构成的。具体代码。时间复杂度O(n)，空间复杂度O(n)。这种解法调用了string::find函数，底层还是通过KMP实现的（不同语言也可能会调用其它方法，如暴力或者BM等平均时间复杂度更好的方法），但效率不如上一个方法高。

总结

字符串的题目包含双指针法、局部+整体翻转法、KMP法等，根据具体问题具体分析，采取合适的方法完成解题。

文中部分内容参考自：代码随想录​​​​​​​

补充题

1. Leetcode 1392 最长快乐前缀

难度：⭐️⭐️⭐️

做完实现strstr()题目后，这道题就很简单了，可以看做一个迷你版的strstr()。只需要遍历一遍整个字符串，得到next数组，那么这个数组的最后一个元素的值就是最大前后缀的个数。KMP具体代码：时间O(n) 空间O(n)。

本题也可以用串哈希来做，分别从两端开始遍历，计算经过的子串的哈希值，返回相同值的最大子串长度。具体代码​​​​​​​。时间O(n) 空间O(1)。