计算机组成原理 new08 电路 $\color{red}{Δ}$

ALU

在计算机中，二进制数据的运算和传输都是使用高低电平信号来进行传输的，高电平代表二进制的1，低电平代码二进制的0。

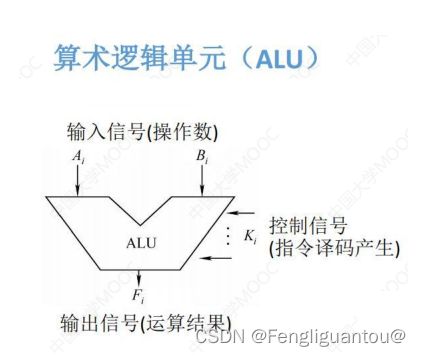
ALU：ALU是一种组合逻辑电路，能够进行算术运算和逻辑运算，因为加减乘除都能转换成加法的运算，所以ALU的核心是带标志加法器(实际上加法器内部的运算又都是采用的逻辑运算为基础)。在ALU中，有两个输入端输入高低电平信号(即操作数)，一个输入端输入CU发送的控制信号，一个输出端输出信号(运算的结果)。

实际ALU的物理结构是这样的：

其中 $B_0-B_3$ 4根线可以输入4个信号，即4bit的二进制信息，作为ALU的第一个操作数
同样 $A_0-B_3$ 4根线可以输入4个信号，即4bit的二进制信息，作为ALU的第二个操作数
机器字长就是ALU的宽度，即ALU输送操作数使用的数据线的条数，图中ALU的宽度为4，即机器字长为4。
M用于传输CU发送的控制信号，M=0表示算术运算，M=1表示逻辑运算。
$S_0-S_3$共4根数据线，每次可以传输4bit的信息，所以最多可以表示16个不同的状态。即每个类型的运算支持的种类，例如M=0，即支持16种算术运算。
其中 $F_0-F_3$ 4根线输出运算的结果

基本逻辑运算

事实上，计算机中的运算大多是由逻辑运算为基础完成的。

逻辑运算和普通的加减法一样支持分配律和结合律

逻辑运算中使用分配律和结合律有什么意义？

对电路进行简化，减少成本。
例如：

复合逻辑的运算

其中异或门可由与或非门组成,并且异或门常用于实现加法和奇偶校验：

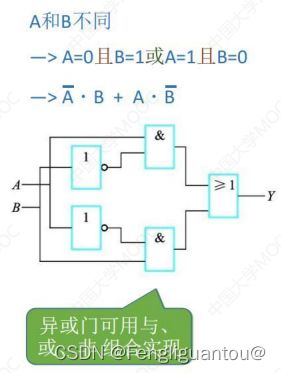
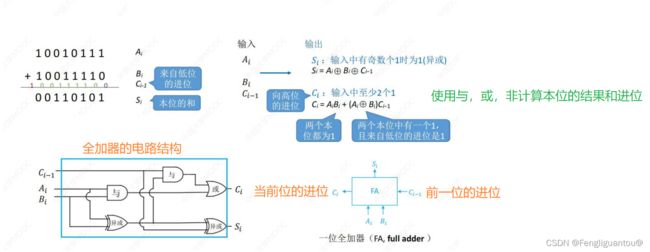
一位全加器

本位和：本位和=当前位的操作数1+当前位的操作数2加上前一位的进位信息。

串行加法器

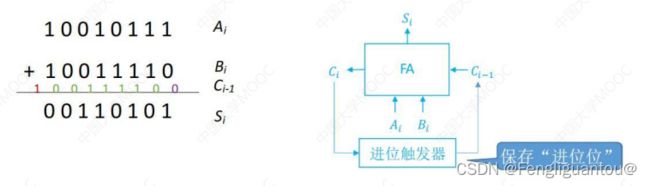
当串行加法器只有一个全加器的时候就可以看作是全加器。

构成：串行加法器由一个一位全加器组成。

特点：进位信息串行传输，当前位的进位信息需要等上一位运算完以后才能获取，并且每次只能输入两个操作数

运行原理如下：
$C_i$每次存储前一位的进位信息，当进行运算的时候$C_i$会将前一位的进位信息传输给$C_{i-1}$，$C_{i-1}$和 $A_i,B_i$进行当前位的运算，然后再将运算的结果从$S_i$输出并将进位信息输出给$C_i$。

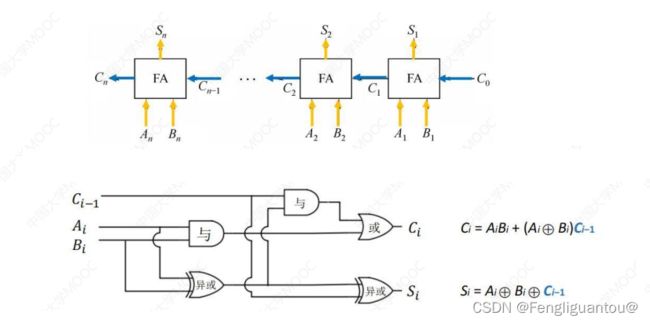
串行进位的并行加法器

构成：串行进位的并行加法器由多个一位全加器构成，也叫做串行进位加法器，其中串行进位又叫做行波进位。这里说的串行进位就是进位信息的串行运输的。

运行原理如下：当前位的进位信息会通过数据线传送到下一位参与运算。

特点：进位信息串行运输，当前位的计算需要等待上一位计算完成并且传输进位信息才能开始，因为有多个全加器所以可以并行的同时输入所有的操作数。因为串行进位的并行加法器中加法器的数量有限，所以最终最高位的进位是被舍弃的，所以这个实际上就等于是一个模 $2^n$的加法运算，即结果最多只能有n位。

特点：因为高位的计算收到低位进位信息的限制，所以运算时间主要是由进位信息的传递时间决定的，位数越多就会导致延迟时间越长(这里的延迟应该理解为后面的加法器需要等待进位信息的时间)，全加器本身对于本为和计算速度或者延迟是可以忽略的。所以关键是提高进位的产生速度和进位信息的传递速度

并行进位的并行加法器(全先行进位加法器)

并行进位的并行加法器可以看作是串行进位的并行加法器的一个优化：
在串行进位的并行加法器中，当前位的运算需要等待前一位完成才能开始执行，其进位信息是从前往后逐步进行传输的，这就会导致后面的全加器很大的一段时间中都是空有数据，没有进位信息，即是处于空闲状态的，而并行进位的并行加法器正是对进位信息这一环节进行了优化，并行进位的意思就是进位信息并行产生。

优化思路：
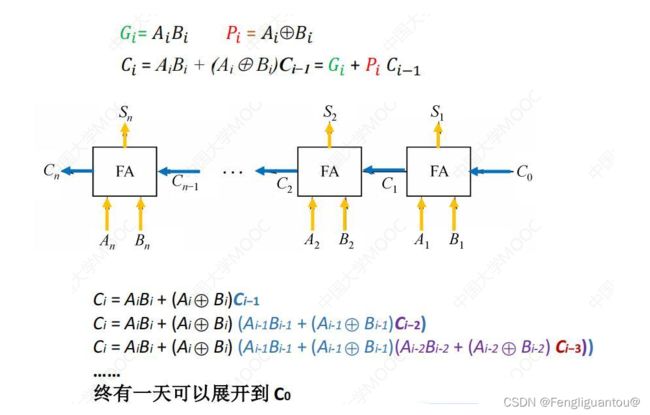
我们知道，我们是根据逻辑表达式得出当前的进位信息，而当前的进位信息依赖上一位的进位信息，我们对进位信息的表达式完全展开可以发现一个规律：
处于$B_i$，$A_i$位置的全加器，只需要依赖$A_1-A_{i-1}$和$B_i-Bi-1$加上$C_0$就可以得出$A_i$位置需要的进位信息，而$A1-An，B1-Bn$还有$C_0$我们都是一开始就已知的，所以这样一来可以根据表达式提前算出每个全加器需要的进位信息。

运行原理：我们可以使用CLA部件完成上述进位信息的计算，假设操作数为4位的长度，那么我们就可以使用4位CLA部件完成上述进位信息的计算。从图中我们可以看出，我们先将所有的操作数共同送入对应的加法器，并且将$C_0$ \color{red}{} 送入第一个加法器和CLA内部。所有的加法器在内部先计算出自己的$G_i$和$P_i$，然后将$G_i$和$P_i$送入CLA内部，最后CLA对这些数据进行整合，算出所有加法器需要的进位信息，同时输送到加法器内部。($G_i$和$P_i$的运算不依赖进位信息，所以可以先在加法器内部完成)。

注:CLA也叫做先进进位(超前进位)部件。

特点：因为通过表达式的优化，每个全加器需要的进位信息只和$B_i$，$A_i$和$C_0$有关，所以相互间的进位没有依赖关系，只要所有操作数$B_i$，$A_i$和$C_0$同时到达，CLA就几乎可以同时算出进位信息，并且将进位信息传输到对应的加法器内部，每个加法器可以同时生成自己的对应位的结果。进位方式快速，得到进位信息的速度和操作数的长度无关。(这个不好理解，对此我们应该以正常情况下正常的操作数长度进行理解)


对于进位的式子，我们还需要进行一些剖析，当前位是否产生进位有两种可能：
1.$A_i和B_i$都是1，我们将其记作 $G_i$，我们将其叫做进位产生信号。
2…$A_i和B_i$其中有一个是1，然后前一位的进位是1。所以如果要满足第二个条件，那么就需要$A_i$^$B_i$=1，将其记作$p_i$，将其叫做进位传递信号。
$C_i$的进位，需要$p_1-p_i,G_1-G_i和C_0$才能算出。

注意：当并行进位的并行加法器支持的操作数长度越长时，就需要更多的进位信息，就会导致后面处理进位信息的表达式越来越复杂，即内部电路实现更加复杂。所以一般来说支持操作数长度最长为4的并行进位的并行加法器可以完成进位信息的同时输入，进位信息同时输入到对应的全加器位置上。

虽然说，全进位加法器(并行进位的并行加法器)收到操作数位数的限制，但是我们依旧有解决方法，可以使用串联的方式将全进位加法器进行串联，例如串联两个4位全先行进位加法器，通过这样的方式，我们可以达到：组内进位并行传输，不同组的进位信息串行传输，只不过后面的组需要等前一组算完进位信息并且传输过来，才能开始计算。

如果想要更快，可以采用两级或者多级先行进位加法器

这个明天再写。

加法电路原理总结

实际上在计算机中，加法和减法都是通过加法电路完成的，而加法电路的本质是使用异或门来完成，异或可以采用与或非电路完成。

ALU和加法器有什么关系

我们说了这么多加法器和ALU，两者的联系是什么？
ALU叫做算术逻辑单元，其能够实现逻辑运算和算术运算。可以将其看作是一个大盒子，里面可能有加法器进行加法运算，减法器，等等部件。而ALU就是存储这些运算部件的一个盒子。
但是需要非常注意的是，ALU是一个包含了加法器之类的集合，但是这个集合里面没有寄存器！这个非常重要，寄存器都是在ALU内部的，ALU没有存储功能！在某些情况下，移位操作可能是在ALU内完成，也有可能是在ALU外的移位寄存器内完成。并且ALU不是一定要进行运算，ALU也可以做为一个中间介质，进行数据的流动，例如MDR的数据可能需要通过ALU流动到其他寄存内。

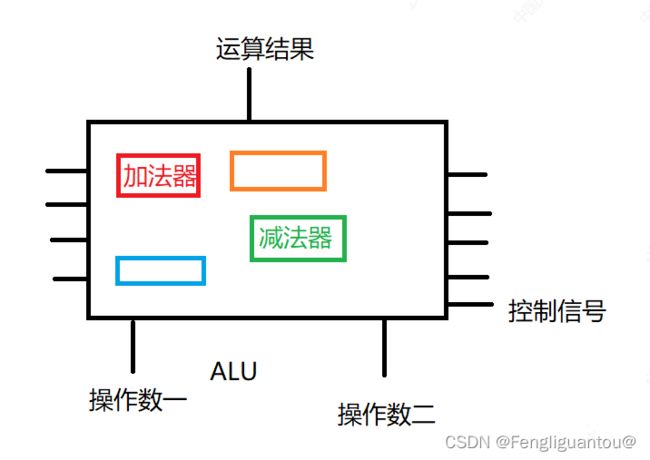
加法器原理

一个普通的加法器模型如下，其内部具体是全加器，还是并行进位的并行加法器，或者是其他细分类型的加法器，应该都是可以的。

这种加法器原理如下：
1.加法器右端
加法器右端会cin输入一个低位的进位。这里的进位应该和我们前面说的进位信息分开，因为这个进位可能不只是进位信息这一层含义，其可能还具有其他含义，例如使用这个进位可以完成求补的部分操作。这个进位参与最低位的运算。
2.加法器左端
左端会输出运算以后，最高位的进位。这个进位可能是进位信息，也有可能具有其他的含义，例如这个进位可以作为判断数据计算是否有溢出等等。
举个例子：

因为这种加法器具有的特性，所以有时候我们可以将两个加法器进行拼接，达到扩展功能。例如：

所以通过这种扩展的功能可以用于并行进位的并行加法器，即每个4位，然后进行扩展，就能更好的发挥并行进位的并行加法器的功能，这个实际上就是我前面说的并行进位加法器的串联。

ALU总结

ALU内没有寄存器，ALU没有存储功能，所以ALU内没有寄存器这些东西，所以ALU需要搭配外部的寄存器完成运算功能。

无符号整数/补码加减法加法器

这里为什么我们没说原码和反码，

因为原码和反码的符号位不能参与运算，我们接下来的计算是需要符号位参与的。

这里的说的加法器可以除了可以完成有符号补码整数和无符号整数的加减运算，可以完成有符号补码小数的加减法运算吗？

可以的，因为计算机内部并没有设置小数点，小数点是人为的，所以计算机内部运算的时候只关心数据的符号位和数值位

  $(1)$补码加减法加法器

补码加减法加法器实际上是在上一个加法器的基础上，添加了一些玩意制造成的，其模型如下：
运行原理如下：
1.CU会发送一个sub控制信号至cin和多路选择器。当执行加法时信号为0，减法信号为1。
2.X和Y为两个操作数的输入端口，多路选择器会根据信号为0为1选择导通的线路，被加数可以直接从X端口输入到达加法器，加数Y只能通过多路选择器中导通的接口达到加法器内。

对此我们分为补码加法和补码减法：
  $(1)$补码加法

因为补码加法可以直接执行，所以执行过程很简单：
1.通过X和Y输入被加数和加数，不知道是不是CU发送0sub信号给多路选择器和cin，多路选择器收到信后导通0号线路让加数进入加法器，最后在加法器内部进行运算即可。

  $(2)$补码减法

补码减法比较特殊，需要对减数进行求补，并且让减法变成加法。求补的本质操作数是所有位按位取反，末尾加1，因为多路选择器和cin的存在，当执行减法时，减数在参与运算的时候会完成求补这一操作，现在我们来看下具体原理：
1.通过X和Y输入两个操作数，不知道是不是CU发送1sub信号至cin和多路选择器。多路选择器导通1号线路，在多路选择器的1号线路中有一个非门，其会对被减数进行全部位取反，所以减数到达加法器内部时，求补工作已经完成一半，随后因为cin会参与最低位的运算，并且cin是1，所以求补需要的所有工作全部完成，即可开始正常的运算。

  $(2)$无符号整数加减法加法器
事实上无符号整数的加减法和补码加减法采用相同的加法器，因为两者的运算逻辑都是相同的，加法时直接按位相加即可，减法都是进行减数求补 ，然后减法变加法，所以两者的本质运算逻辑相同，所以这个加法器适用于无符号整数的加减法。但是需要注意的是因为无符号整数和补码的区别，两者的解释方式和进位溢出的判断方式具有差别，例如：
下面输入了两组操作数进行运算，最终得到的二进制序列相同，但是因为无符号整数和补码的特性不同，导致两者的运算结果出现了差异：

所以可以得出结论：
无符号整数和补码进行加减法时可以使用同一套电路主体，但是解释方式和溢出标志位等判断一定存在区别。

标志位的生成

前面我们说了，补码的加减法和无符号数的加减法可以使用同一套电路，但是因为两者的特性不同，对于溢出的判断和数据运算结果的解释和判断一定需要不同的处理机制，而在计组中，底层使用了标志位来分别进行判断：
事实上，加法器在运算以后不仅要输出运算的结果还有cout，还需要输出4个标志信息，分别是OF,SF,ZF,CF。
需要注意的是：无论是有符号整数的运算还是无符号整数的运算都需要输出这4个标志位的信息，但是标志信息是否具有意义就需要根据数据的类型即有符号或者无符号来进行决定。

现在我们给出四个标志位的计算方式：

现在我们开始验证为什么能够通过上述的方式判断数据是否溢出，为正数还是负数，是否溢出/借位。
首先在验证之前，我们需要明确一个知识点：

什么叫做溢出？

事实上，溢出指的是n位数值能够表示的范围溢出，例如nbit位可以表示最大的数字是127，这时结果出现了128，这时就叫做溢出，但是需要注意的是比特位的溢出并不一定代表数值的溢出，这是非常需要注意的，所以我们这里的OF溢出，实际上验证的数值是否溢出范围。

  $(1)$OF判断溢出的根据

首先，有符号的计算中，无论是什么加法运算还是减法运算，最后都被转换成了加法运算，首先需要知道的是，在将减法转换成加法的这个过程中，求补动作的比特位溢出是否会对减数具有影响，既然是减数比特位溢出，那就只有一种情况，即减数是全0，只有如此在经过求补以后才会比特位溢出，当减数全0时0，经过求补以后，得到的依旧是全0，因为0的真值就是0，全0对被减数不产生任何影响，所以这个比特位溢出对于接下来的运算是没有影响。所以除0以外的正数求补后一定是负数，负数求补以后一定是正数，虽然0作为例外，但是0对于运算不会产生影响，所以可以不用管。

在明白了这个以后，开始列举补码计算可能会出现的情况
所以一共会出现以下四种情况：
正数+正数
正数+负数
负数+正数
负数+负数

其中正数+负数和负数+正数因为是正常的计算，所以一定不会溢出。
所以只有可能正数+正数和负数+负数的这个过程产生溢出。

现在我们对这两种情况再次进行分析：
首先因为是正数+正数，所以cout位的进位一定是0，因为一开始两个正数的符号位都是0，所以即使次高位的进位是1，cout位的进位也一定是0。所以也就是说在正数+正数中，cout位的进位一定是0，所以如果数据发生溢出，根据OF的运算原理，那么次高位的进位就需要是1。我们看下如果次高位的进位是1会发生什么。按正常情况下，没有溢出的情况来说，正数+正数得到的符号位必须是0，因为补码的最高位代码符号位。一旦符号位出现1，则说明结果变成了负数，而这个1一定是次高位的进位。所以说在正数+正数中，一旦COUT^次高位进行=1，则说明数值发生了溢出。

分析完正数以后，负数就简单了，负数+负数时，cout位的进位一定是1，因为两个负数相加，最高位都是1，那么就会发生进位1，如果次高位不产生进位1，就会导致结果中最高位是0，0代表正数，而负数+负数不可能得到正数，所以说如果不溢出，要求次高位的进位一定是1。

所以我们可以总结出结论：
正数+正数：不溢出的情况下，cout和次高位进位都等于0
负数+负数：不溢出的情况下，cout和次高位进位都等于1
所以一旦cout^cin=1，则说明发生了溢出。

溢出以后，结果是怎么样的？

如果是两个正数溢出，那么结果是负数
两个负数溢出，结果是正数。

  $(2)$CF判断溢出的根据
CF溢出判断的公式是：cout^sub

CF本质是无符号整数使用的，所以CF也只有两种可能会溢出：

因为在无符号中只有正数的概念：
1.正数+正数
当最高位进位为1时表示溢出，这很好理解，两个正数最高位产生进位了那就是说明存不下了。
而进行加法时，sub=0，所以只要最高位有进位，那就是溢出了。

2.正数-正数
在CF中，对于正数-正数判断溢出我们不需要对减法变成加法，只要判断被减数和减数哪个大即可，被减数小即发生溢出。在减法中，sub为1，那就说明只要进位是0，就发生了溢出，我们思考下是为什么？
我们模拟下不溢出的情况下：
1001
0100

被减数：1001
求补：1100
我们可以看出相加以后最高位的进位肯定是1。

补码加减法发运算的溢出判断

  $(1)$
其实本质也是OF，因为只有正数+正数和负数+负数才可能溢出，所以只需要判断计算前的操作数符号和计算后结果的符号是否相同即可知道有无溢出，相同表示没有溢出，不同表示溢出。当采用一位符号位时，计算机会保留原操作数的符号信息，然后根据得到结果的符号，将两者进行异或。

  $(2)$
前面说的是OF的本质，这里说的就是OF的判断方法。和前面本质都是一样的。

其在计算机底层同样也是采用的异或，将最高有效位的进位和符号位的进位进行异或。
  $(3)$

根据溢出的结论：只有两种可能会导致溢出：
  $(1)$正数+正数

00+00=00，在OF中，次高位的进位一定是0，这样才是没有溢出，所以在双符号位中也是如此，这时次高位是第三位，因为多了一个符号位，但是同样是符号位后的一位。入宫该位的进位是1，就说明溢出 ，00就会变成01。

  $(2)$负数+负数

11+11=10，在OF中，如果负数+负数不溢出，符号位后一位的进位必须是1，如果是1最终得到的符号位就是11，不然就是10说明符号位的进位不是1，说明溢出了。
在计算机中，对于双符号的溢出判断，也是采用异或的，将两个符号位进行异或即可知道是否有发生溢出。

计算机中是如何存储双符号位的？

首先需要知道的是，在计算机中是只存储单符号位的，因为双符号位中两个位的符号相同，所以在存储的时候只需要存储一个，在进行计算的时候，ALU会保存其中一个符号位，然后使用计算结果和保留下来的符号位进行异或判断。

双符号位是如何完成算术移位的？

因为计算机中实际不存储双符号位，只存储一个符号位，所以在进行移位的时候只有次高位的符号位即单符号位参与移位。

溢出电路判断总结

前面说的三种溢出电路，本质都是使用异或来进行溢出判断的。

溢出和真值的关系

因为只有补码的符号位可以参与运算，所以这里我们只需要考虑补码。

只有两种运算会溢出：
正数+正数
负数+负数

这两种情况可能由两个状态迁移而来：
这两个状态是真值原本的状态，但是因为计算机的减法都变成了加法
正数-负数
负数-正数
所以两个状态变成了
正数+正数和负数+负数
而在真值中，正数-负数得到的也是正数+正数，负数-正数本质也是负数+负数。
所以补码的计算方法和真值是严格对应的，所以在有真值的前提下可以使用真值来判断是否溢出，例如下面这题：

8位补码可以表示最小数和最大数分别是-128，127。
所以可以直接计算每个选项的真值，然后判断是否落在区间内。
结果是x-y=103+25=128，不在区间内，所以溢出。