一篇文章带你彻底理解运用栈和队列,超详细千字总结对比.
published: true
date: 2022-1-22
tags: ‘算法与数据结构’
栈和队列
本章主要介绍并用cpp代码从零实现了栈和队列两个数据结构,同时引出了递归以及栈帧(函数调用)的介绍,以及对栈和队列的相关经典问题的解决,如运算符优先数法、地图四染色、子集划分问题等。
可以转载,但请声明源链接:文章源链接justin3go.com(有些latex公式某些平台不能渲染可查看这个网站)
栈
基础概念
| 定义 | 只能在表的一端进行插入和删除的线性表 |
|---|---|
| 逻辑结构 | 数据元素之间是一对一的关系 |
| 存储结构 | 顺序存储或链式存储 |
| 运算规则 | 只能在栈顶运算,且访问结点时依照后进先出(LIFO)或先进后出(FILO)的原则 |
| 基本操作 | 建栈、判断栈满或栈空、入栈、出栈、取栈顶元素值 |
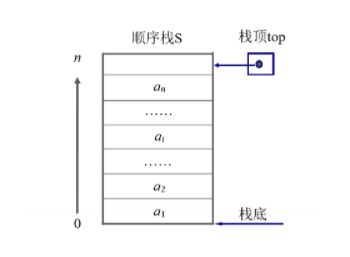
顺序栈
定义:利用一组地址连续的存储单元,依次存放从栈底到栈顶的数据元素。
P U S H : s − > e l e [ s − > t o p + + ] = a n + 1 PUSH: s->ele[s->top++] = a_{n+1} PUSH:s−>ele[s−>top++]=an+1
P O P : ( s − > t o p ) − − , e = s − > e l e [ s − > t o p ] POP: (s->top)--, e = s->ele[s->top] POP:(s−>top)−−,e=s−>ele[s−>top]
注:顺序栈不仅需要判断下溢(栈空),还需要判断上溢(栈满)。
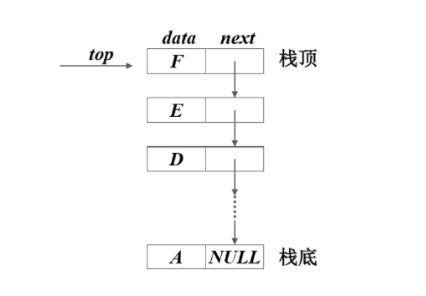
链式栈
定义:栈的链式存储结构,简称链栈;与单链表类似链表的尾部是栈底,链表的头部是栈顶。
栈的应用
运算符优先数法
问题:对算术表达式求值:1 + 2 * 4 - 9/3
解法
-
对每种运算符赋予一个优先数,如:
* / + - # 2 2 1 1 0 -
其中#是表达式结束符。
-
一般设两个栈:
- 运算符栈(OPTR):存放运算符。
- 操作数栈(OPND):存放操作数。
中缀表达式a + b*c + (d * e + f) * g,其转换成后缀表达式则为a b c * + d e * f + g * +。转换过程需要用到栈,具体过程如下:
1)如果遇到操作数,我们就直接将其输出。
2)如果遇到操作符,则我们将其放入到栈中,遇到左括号时我们也将其放入栈中。
3)如果遇到一个右括号,则将栈元素弹出,将弹出的操作符输出直到遇到左括号为止。注意,左括号只弹出并不输出。
4)如果遇到任何其他的操作符,如(“+”, “*”,“(”)等,从栈中弹出元素直到遇到发现更低优先级的元素(或者栈为空)为止。弹出完这些元素后,才将遇到的操作符压入到栈中。有一点需要注意,只有在遇到" ) “的情况下我们才弹出” ( “,其他情况我们都不会弹出” ( "。
5)如果我们读到了输入的末尾,则将栈中所有元素依次弹出。
#include地图四染色
栈的特性:
- 在某些问题的求解中常使用试探方法,当某一路径受阻时,需逆序退回,重新选择路径。
- 可利用栈记录曾到达的每一状态,栈顶状态即是回退的第一站。
问题:用不多于四种颜色对地图着色,使相邻地区不重色。
解法:
- 从1号地区开始逐一染色每一个地区逐次用色号1、2、3、4进行试探。
- 若当前所取的色号与周围已染色的地区不重色,则用栈记下该地区的色号,否则依次用下一色号进行试探。
- 若出现用1~4色均与相邻地区重色,则需退回,修改上一地区的色号:退栈回溯,修改当前栈顶的色号。
detail:
使用一个关系矩阵存储地区与地区之间是否相邻
伪代码:
for r in range(p): # p为1~7的城市号
for ci in range(c): # c为1~4的色号
for r in range(p): # 依次试探相邻城市是否染过颜色ci
step:{是:回退;否:染色}

/**gb2312**/
#include
if(map[i][j] == 1){
relationship.push_back(j);
}
}
return relationship;
}
void print_vec(vector<int> vec){
cout << "<";
for(int i = 0; i < vec.size(); i++){
cout << "{"<< name[i] << ": " << vec[i] << "}" << ", ";
}
cout << ">" << endl;
}
//非递归解法
void solution1(){
vector<int> color_stack;
vector<int> temp;
int i=0, c=0, k=0;//i为所有城市,c代表4种颜色
for(; i < 34; i++){//涂第i个城市
temp.clear();
temp = find(i);//temp为与当前i有关系且已经涂过色的城市
for(;c < 4; c++){
int flag1 = 0;
if(!temp.empty()){
for(int m = 0; m < temp.size(); m++){
if(color_stack[temp[m]] == c){
flag1 = 1;//说明当前颜色不能用
}
}
}
if(flag1 == 0){//涂色
color_stack.push_back(c);
c = 0;
break;
}
}
while(c == 4){//没有颜色可用,向上判断一次
c = color_stack.back() + 1;
color_stack.pop_back();
temp.clear();
temp = find(color_stack.size());
while(c < 4){//遍历后面几种颜色进行涂色
int flag2 = 0;
if(!temp.empty()){
for(int m = 0; m < temp.size(); m++){
if(color_stack[temp[m]] == c){
flag2 = 1;//说明当前颜色不能用
}
}
}
if(flag2 == 0){//涂色
color_stack.push_back(c);
c = 0;
break;
}
c++;
}
}
}
print_vec(color_stack);
/*<{广西: 0}, {广东: 1}, {云南: 1}, {贵州: 2}, {湖南: 3},
{江西: 0}, {福建: 2}, {浙江: 1}, {安徽: 2}, {湖北: 1},
{重庆: 0}, {四川: 3}, {西藏: 0}, {青海: 1}, {新疆: 2},
{甘肃: 0}, {陕西: 2}, {宁夏: 1}, {内蒙: 3}, {北京: 0},
{黑龙江: 0}, {吉林: 1}, {辽宁: 0}, {天津: 1}, {河北: 2},
{山西: 0}, {河南: 3}, {江苏: 0}, {山东: 1}, {上海: 2},
{海南: 0}, {台湾: 0}, {香港: 0}, {澳门: 0}, >
*/
}
// 递归解法
int isOk(int metrix[34][34],int city[34],int current){
for(int j=0; j<current; j++)
if(metrix[current][j]==1&&city[j]==city[current])
//他们之间是相邻且涂的是同一种颜色
return 0;
return 1;
}
void color(int metrix[34][34],int city[34],int sum,int current)
{
if(current<=sum){
for(int i=0; i<4; i++) //colored current city
{
city[current]=i;
if(isOk(metrix,city,current))
{
color(metrix,city,sum,current+1); //colored next city
break;
}
}//注意这个循环和递归的结合,挺巧妙的。
}
}
int main (){
//solution1:
cout << "****************1***************" << endl;
solution1();
//solution2:
int city[34] = {};
color(map,city,34,0);
//print
cout << "****************2***************" << endl;
cout << "<";
for(int i = 0; i < 34; i++){
cout << "{"<< name[i] << ": " << city[i] << "}" << ", ";
}
cout << ">" << endl;
//结果一致
// for(int i = 0; i < 34; i++){
// cout << city[i] << ", ";
// }
//color = [0, 1, 1, 2, 3, 0, 2, 1, 2, 1, 0, 3, 0, 1, 2, 0, 2, 1, 3, 0, 0, 1, 0, 1, 2, 0, 3, 0, 1, 2, 0, 0, 0, 0]
return 0;
}

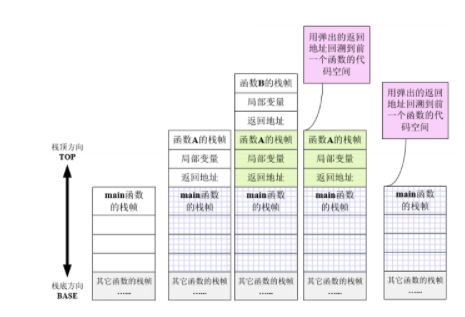
函数调用
- 栈是存储器的一个区域。
- 一般使用栈实现函数调用。
- 函数占用的区域被称作函数的栈帧。
- 函数调用时,为被调用的函数分配栈帧,存放函数创建的局部(临时)变量等信息。
- 函数嵌套调用时,堆栈中会同时存在多个函数的栈帧。
递归
定义:若一个过程直接地或间接地调用自己,则称这个过程是递归的。
分类:直接递归与间接递归。
条件:
-
解决问题时,可把一个问题转化为一个新的问题。
-
这个新问题的解法与原问题的解法相同,只是所处理的对象不同。
-
必须有结束递归的条件,否则递归将无休止地进行,导致耗尽系统资源。
-
数据结构是递归的,如二叉树。
-
问题的解法是递归的,如汉诺塔、地图四染色、走迷宫等。
-
大问题转换为几个小问题,小问题进一步分解为更小的小问题,直到递归出口为止。
-
递归模型由递归出口和递归体两部分组成,前者确定递归合适为止,后者确定递归的方式。
n ! = { 1 , n = 0 n ∗ ( n − 1 ) ! , n > = 1 n! = \begin{cases} & \text 1 ,n=0\\ & \text n*(n-1)!, n>=1 \end{cases} n!={1,n=0n∗(n−1)!,n>=1
-
递归算法的非递归描述:考虑到**栈帧的模型(系统栈的调用)**就很好理解。
\********递归解法********\
int fac(int n){
if(n == 1)
return 1;
else
return n*fac(n-1);
}
int main(){
fac(4)
return 0;
}
\*******非递归解法*******\
int fac(int n){
int s = 1;
while(n >= 1)
push(stack, p--);
while(!empty(stack))
s *= pop(stack);
return s;
}
int main(){
fac(4);
return 0;
}
两种解法的时间复杂度与空间复杂度都是一样的。
队列
基础概念
| 队列定义 | 只能在表的一端进行插入,在表的另一端进行删除的线性表 |
|---|---|
| 逻辑结构 | 元素之间是一对一的关系 |
| 存储结构 | 顺序队列和链队列 |
| 运算规则 | 队尾入队、队头出队、遵循先进先出(FIFO)的原则 |
| 基本操作 | 入队、出队、建空队列、判队空或对满 |
顺序队列
队列的顺序存储,称为顺序队列。由存放元素的顺序表、队头指针、队尾指针三部分组成。
顺序存储的两个问题:
-
普通队列出现的假上溢的问题:使用循环队列解决:
-
队空与队满的判定条件相同:少用一个元素空间
- 队空:front == rear
- 队满:(rear + 1)%M == front
初始化:
cquenetp *initquene(){
cquenetp *q;
q = new cquenetp;
//将队列头尾指针置为0
q->front = q->rear = 0;
return q;
}
入队:
if((q->rear+1)%M == q->front){ //判队满
q->rear = (q->rear+1)%M; //入队
q->v[q->rear] = x;
return true;
}else{
return false;
}
出队:
if(q->front == q->rear){ //判队空
q->front= (q->front + 1)%M; //出队
x = q->v[q->front];
return x
}else{
return false;
}
链队列
- 头指针(front)指向队头结点。
- 尾指针(rear)指向队尾结点。
- 注意是删头加尾,因为删除链表的一个结点需要知道它的前趋结点。

- 链为空的条件是front == rear, 原则上来说链队列是不需要判满的。
初始化:
linkquene *initquene(){
linkquene *q;//链队列指针,封装了队头队尾指针
QUENE *p;//p为指向链队列结点的指针
q = new linkquene;
p = new QUENE;//生成头结点
p->next = NULL;//头节点指针域为空,空队列
q->front = q->rear = p;//队头队尾指针都指向头结点
return q;
}
入队:
void enquene(linkquene *q, datatype x){
QUENE *p; //p为指向链队列结点的指针
p = new QUENE;
p->data = x;
p->next = NULL;
q->rear->next = p;
q->rear= p;
}
出队:
datatype dequene(linkquene *q){
QUENE *p; //p为指向链队列结点的指针
datattype x;
if(q->front == q->rear){
return false;
}else{
p = q->front->next;//p指向队列头
x = p->data;//将队头元素的值赋给x
q->front->next = p->next;//出队
//若出队列后队列为空,则修改队尾指针
if(p->next == null)
q->rear = q->front;
delete(p);
return x;
}
}
队列的应用(子集划分问题)
运动会设立了n个比赛项目,没饿过运动员可以参加1~3个项目。请问应该如何安排比赛日程?从而使同一运动员参加的项目不能在同一时间进行,并使总的竞赛日程最短。
解决方法概述:
将集合A中的所有元素放入一个队列中,然后依次取出队头元素a_i放入一个待分配的组gm中,若a_i与组gm中的其他元素无冲突,则加入组gm,如产生冲突,则将重新入队;当遍历考察一轮队列中的所有元素后,产生一个无冲突的子集gm,如此循环,直到所有元素都被分配完成。
细节:
- 同样使用关系矩阵存放冲突关系
- 使用**newrela[]**存放与当前子集的元素冲突的关系元素==>存一个元素到该子集就将该元素所有有冲突关系的元素在newrela[]中标为1,如此累积,直到这次循环结束,newrela[]清空。

- 是将A中元素的编号(1,2,3······,n)入队到cq中,reault[],newrela[]清空,组号group=1,pre=1。
- 出队一个元素->i,pre = i,result[i] = group,判断冲突。
- 如果i
准备
#include顺序存储实现队列
class my_quene{
int nums[10];
int front = 0;
int rear = 0;
public:
my_quene(){
}
~my_quene(){
}
void enquene(int x){
if((this->rear+1)%10 == this->front){
throw std::out_of_range( "duiman~" );
}
this->rear = (++this->rear)%10;
this->nums[this->rear] = x;
return;
}
int dequene(){
if(this->front == this->rear){
throw std::out_of_range( "duikong~" );
}
this->front = (++this->front)%10;
int x = this->nums[this->front];
return x;
}
int empty(){
if(this->front == this->rear){
return 1;
}
else{
return 0;
}
}
//为该题单独封装的一个方法
//判断一次是否遍历完了
int over(){
//这里后面还要出队入队才算结束
if(this->nums[(this->front + 1)%10] < this->nums[this->rear]){
return 1;
}
return 0;
}
};
链式存储实现队列
struct qnode
{
int key;
qnode* next;
qnode(int x) :
key(x), next(NULL) {
}
};
class my_quene{
qnode* front = NULL;
//front相当于头节点
qnode* rear = NULL;
public:
my_quene(){
front = new qnode(-1);
rear = front;
}
~my_quene(){
delete(front);
}
void enquene(int x){
qnode* temp = new qnode(x);
rear->next = temp;
rear = rear->next;
}
int dequene(){
if(this->empty()){
throw std::out_of_range("quene_empty!");
}
qnode* temp = front->next;
//这里最后一个节点删除的时候需要手动移动rear指针;
if(temp->next == NULL){
rear = front;
}
front->next = temp->next;
int x = temp->key;
delete(temp);
return x;
}
int empty(){
if(rear == front){
return 1;
}
return 0;
}
int over(){
if(this->empty()){
return 2;
}
if(front->next == NULL){
return 0;
}
if(front->next->key < rear->key){
return 1;
}
return 0;
}
};
测试
void test_my_quene(){
my_quene test;
for(int i = 0; i < 4; i++){
test.enquene(i);
}
for(int i = 0; i < 4; i++){
int temp = test.dequene();
cout << temp << ", ";
}
cout << endl;
}
添加冲突
int add_rela(int i){
//如果和当前组冲突,就返回0
if(newrela[i] == 1){
return 0;
}
//不冲突就增加当前会冲突的,返回1
for(int j = 1; j < 10; j++){
if(matrix[i][j] == 1){
newrela[j] = 1;
}
}
return 1;
}
主函数
int main(){
//test_my_quene();
vector<vector<int>> groups;
vector<int> group;
//init_quene
my_quene match;
for(int i = 0; i < 9; i++){
match.enquene(i+1);
}
int temp = 0;
int flag = 1;
int flag_1 = 0;
while(!match.empty()){
while(1){
if(match.empty()){
break;
}
if(match.over()){//标志着一轮结束了,下一步就是这个
if(flag){//说明是开始就不跳出
flag = 0;//下一次是结束
}else if(flag_1){
flag = 1;//下一次是开始
flag_1 = 0;
break;
}
}
temp = match.dequene();
if(add_rela(temp)){
group.push_back(temp);
}else{
match.enquene(temp);
flag_1 = 1;
}
}
//清空关系
for(int i = 0; i < 10; i++){
newrela[i] = 0;
}
if(match.empty()){
break;
}
groups.push_back(group);
group.clear();
}
//展示
for(int i = 0; i < groups.size(); i++){
cout << "{";
for(int j = 0; j < groups[i].size(); j++){
cout << groups[i][j] << ", ";
}
cout << "}, ";
}
cout << endl;
return 0;
}
