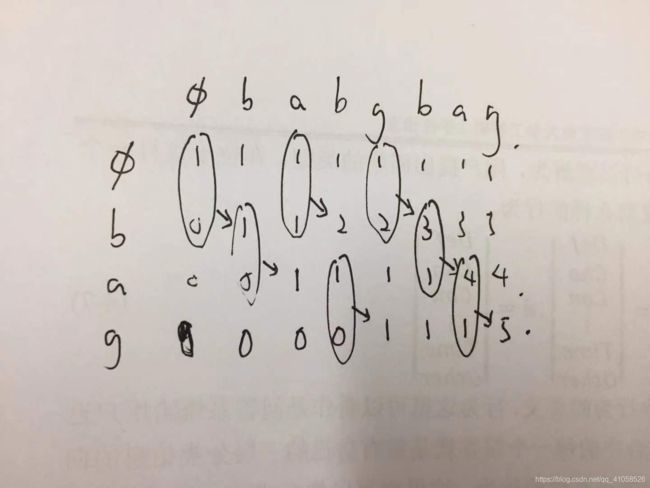leetcode(10) || 动态规划 && 位操作
目录
动态规划
Triangle(mid)
Maximum Subarray(easy)
Maximum Product Subarray(mid)
Longest Increasing Subsequence(最长递增序列)(mid)
Palindrome Partitioning II(分割回文串)(hard)
Maximal Rectangle(最大矩形)(hard)
Best Time to Buy and Sell Stock III(hard)
Best Time to Buy and Sell Stock with Cooldown(hard)
Minimum Path Sum(mid)
Interleaving String(hard)
Scramble String
Decode Ways(mid)
Distinct Subsequences(hard)
Word Break(mid)
Word Break II(hard)
Dungeon Game
House Robber(打家劫舍)(easy)
House Robber II(mid)
House Robber III(hard)
Range Sum Query - Immutable(easy)
range Sum Query 2D - Immutable(medium)
位操作
Number of 1 Bits(easy)
Reverse Bits(easy)
Repeated DNA Sequences(medium)
Gray Code
Single Number(easy)
Single Number II(mid)
Single Number III(mid)
Power of Two
Missing Number(easy)
Maximum Product of Word Lengths(mid)
Bitwise AND of Numbers Range
Power of Three(easy)
动态规划
注意点:
对于一部分的计算,可以把已经算过的节点用哈希表保存起来,以后递归调用的时候,现在哈希表里找,如:Word Break II,House Robber III
Triangle(mid)
Given a triangle, find the minimum path sum from top to bottom. Each step you may move to adjacent numbers on the row below.
For example, given the following triangle
[
[2],
[3,4],
[6,5,7],
[4,1,8,3]
]
The minimum path sum from top to bottom is 11 (i.e., 2 + 3 + 5 + 1 = 11).
Note:
Bonus point if you are able to do this using only O(n) extra space, where n is the total number of rows in the triangle.
解法一:从上往下
不新建dp数组,而是直接复用triangle数组,我们希望一层一层的累加下来,从而使得 triangle[i][j] 是从最顶层到 (i, j) 位置的最小路径和,那么我们如何得到状态转移方程呢?其实也不难,因为每个结点能往下走的只有跟它相邻的两个数字,那么每个位置 (i, j) 也就只能从上层跟它相邻的两个位置过来,也就是 (i-1, j-1) 和 (i-1, j) 这两个位置,那么状态转移方程为:
triangle[i][j] = min(triangle[i - 1][j - 1], triangle[i - 1][j])
我们从第二行开始更新,注意两边的数字直接赋值上一行的边界值,那么最终我们只要在最底层找出值最小的数字,就是全局最小的路径和啦
这种方法可以通过OJ,但是毕竟修改了原始数组triangle,并不是很理想的方法。
class Solution {
public:
int minimumTotal(vector>& triangle) {
if(triangle.empty()) return 0;
int h = triangle.size(),res = INT_MAX;
for(int i = 1;i < h;i++){
int len = triangle[i].size();
triangle[i][0] += triangle[i-1][0];
triangle[i][len-1] += triangle[i-1][len-2];
for(int j = 1;j < len-1;j++){
triangle[i][j] += min(triangle[i-1][j-1],triangle[i-1][j]);
}
}
for(int i = 0;i < triangle[h-1].size();i++){
res = min(res,triangle[h-1][i]);
}
return res;
}
}; 解法二:从下往上
这道题要求的是一个从上往下和最小的路径,下一步只能从下一行相邻的数中找。 很显然,从上往下找路径的可能是不断增加的,因此我们考虑从下往上找。
(1)很显然,当只有一行时:
最小值为那一行最小的数。
(2)当有两行时:
最小值为min(第二行中的两个数)+第一行的数。
依次类推,我们从下往上,可以找到某一行某个数到最后一行相应的最小和,即:
result[j] = min(result[j], result[j + 1]) + triangle[size - 2 - i][j];
当循环都第一行时,则是我们所求的从上往下路径的最小和。
class Solution {
public:
int minimumTotal(vector>& triangle) {
if(triangle.empty()) return 0;
int h = triangle.size()-1;
vector res(triangle[h]);
for(int i = h-1;i >= 0;i--){
for(int j = 0;j < triangle[i].size();j++){
res[j] = min(res[j],res[j+1]) + triangle[i][j];
}
}
return res[0];
}
};
Maximum Subarray(easy)
Given an integer array nums, find the contiguous subarray (containing at least one number) which has the largest sum and return its sum.
Example:
Input: [-2,1,-3,4,-1,2,1,-5,4],
Output: 6
Explanation: [4,-1,2,1] has the largest sum = 6.
Follow up:
If you have figured out the O(n) solution, try coding another solution using the divide and conquer approach, which is more subtle.
思路:这题挺简单,贪心即可
class Solution {
public:
int maxSubArray(vector& nums) {
if(nums.empty()) return 0;
int front = nums[0],max_num = front;
for(int i = 1;i < nums.size();i++){
if(front > 0) front += nums[i];
else front = nums[i];
max_num = max(front,max_num);
}
return max_num;
}
}; 解法二:分治
分治法的基本思想是将问题划分为一些子问题,子问题的形式与原问题一样,只是规模更小,递归地求解出子问题,如果子问题的规模足够小,则停止递归,直接求解,最后将子问题的解组合成原问题的解。
对于最大子数组,我们要寻求子数组A[low...high]的最大子数组。令mid为该子数组的中央位置,我们考虑求解两个子数组A[low...mid]和A[mid+1...high]。A[low...high]的任何连续子数组A[i...j]所处的位置必然是以下三种情况之一:
- 完全位于子数组A[low...mid]中,因此low≤i≤j≤mid.low≤i≤j≤mid.
- 完全位于子数组A[mid+1...high]中,因此mid
- 跨越了中点,因此low≤i≤mid
- 跨越了中点,因此low≤i≤mid
因此,最大子数组必定为上述3种情况中的最大者。对于情形1和情形2,可以递归地求解,剩下的就是寻找跨越中点的最大子数组。 Given an integer array Example 1: Example 2: 题意:注意,这里单个数也算product,所以[-4,2]的结果是2 解法一:和上一题解法一思路差不多 不同的是这里需要维护一个正数最大值和一个负数最小值,但是这个做法有个局限就是,当 一个更加简洁的思路: 1. 当遍历到一个正数时,此时的最大值等于之前的最大值乘以这个正数和当前正数中的较大值,此时的最小值等于之前的最小值乘以这个正数和当前正数中的较小值。 2. 当遍历到一个负数时,我们先用一个变量t保存之前的最大值mx,然后此时的最大值等于之前最小值乘以这个负数和当前负数中的较大值,此时的最小值等于之前保存的最大值t乘以这个负数和当前负数中的较小值。 3. 在每遍历完一个数时,都要更新最终的最大值。 Given an unsorted array of integers, find the length of longest increasing subsequence. Example: Note: Follow up: Could you improve it to O(n log n) time complexity? 解法1:O(n*n) LIS算是动态规划中的经典题目,DP中求什么就设什么。我们设dp[i]是在0~i上的LIS的长度。我们现在需要考虑初始条件和转移方程。 (1)初始条件: (2)转移方程: 解法二:O(NlogN) dp数组size为nums.size+1,里面用来存放长度 i 序列最小末尾的数,而后我们只需每次二分查找更新dp即可 。 例: 假设存在一个序列d[1..9] = 2 1 5 3 6 4 8 9 7,可以看出来它的LIS长度为5。 Given a string s, partition s such that every substring of the partition is a palindrome. Return the minimum cuts needed for a palindrome partitioning of s. Example: 重述题意:输入一个字符串,将其进行分割,分割后各个子串必须是“回文”结构,要求最少的分割次数。显然,为了求取最少分割次数,一个简单的思路是穷尽所有分割情况,再从中找出分割后可构成回文子串且次数最少的分割方法。 解题思路:对于输入字符串如s=“aab”,一个直观的思路是判断“aab”是否构成回文,根据回文的特点是对称性,那么,我们可以判断s[0]与s[2]是否相等,不等,因此“aab”不能构成回文,此后再怎么判断呢???这种无章法的操作没有意义,因为一个字符串构成回文的情况是很复杂的,对于一个长度为n的字符串,其构成回文的子串长度可能的长度分布范围可以是1—n:整体构成回文如“baab”,则子串长度可为n=4;如“cab”,只能构成长度为1的回文子串。 鉴于上述分析,对于一个字符串,我们需要考虑所有可能的分割,这个问题可以抽象成一个DP问题。 这里需要两次dp: (1)判断是否为回文字符串 对于一个长度为n的字符串,设 pd[i][j] 表示第i个字符到第j个字符是否构成回文,其状态转移方程为 p[i][j] = (s[i] == s[j]) && p[i+1][j-1],其中 p[i][j] = true if [i, j]为回文 (2)需要切割几次 一维的dp数组,其中dp[i]表示子串 [0, i] 范围内的最小分割数,那么我们最终要返回的就是 dp[n-1]。 我们需要判断区间 [j, i] 内的子串是否为回文串了,是回文串,dp[i] =1 + dp[j-1] Given a 2D binary matrix filled with 0's and 1's, find the largest rectangle containing only 1's and return its area. Example: 思路:这道题的二维矩阵每一层向上都可以看做一个直方图,输入矩阵有多少行,就可以形成多少个直方图,对每个直方图都调用 Largest Rectangle in Histogram 直方图中最大的矩形 中的方法,就可以得到最大的矩形面积。 (1)那么这道题唯一要做的就是将每一层构成直方图,由于题目限定了输入矩阵的字符只有 '0' 和 '1' 两种,所以处理起来也相对简单。方法是,对于每一个点,如果是‘0’,则赋0,如果是 ‘1’,就赋 之前的height值加上1。 (2)对每一行调用计算最大直方图 还有一种方法可参考:https://www.cnblogs.com/grandyang/p/4322667.html Say you have an array for which the ith element is the price of a given stock on day i. Design an algorithm to find the maximum profit. You may complete at most two transactions(最多执行两次交易). Note: You may not engage in multiple transactions(必须先卖出再买入) at the same time (i.e., you must sell the stock before you buy again). Example 1: Example 2: Example 3: 思路: 参考:https://blog.csdn.net/linhuanmars/article/details/23236995 这题很难,这里可以是k次交易 (1)global[i][j]:当前到达第 i 天,可以最多进行 j 次交易(不一定一定要交易到 j 次),最好的利润是多少 global[i][j] = max(local[i][j], global[i - 1][j]) 取当前局部最好的,和过往全局最好的中大的那个(因为最后一次交易如果包含当前天一定在局部最好的里面,否则一定在过往全局最优的里面) (2)local[i][j]:当前到达第 i 天,最多可进行 j 次交易,并且最后一次交易在当天卖出的最好的利润是多少 它们的递推式为: local[i][j] = max(global[i - 1][j - 1] + max(diff, 0), local[i - 1][j] + diff) 第一个是全局到i-1天进行j-1次交易,然后加上今天的交易,如果今天是赚钱的话(也就是前面只要j-1次交易,最后一次交易取当前天),如果今天不赚钱,就让其今天买进再卖出,这样也增加了一次交易,最后一次交易也在今天 第二个量则是取local第i-1天j次交易,然后加上今天的差值(这里因为local[i-1][j]比如包含第i-1天卖出的交易,所以现在变成第i天卖出,并不会增加交易次数,而且这里无论diff是不是大于0都一定要加上,因为否则就不满足local[i][j]必须在最后一天卖出的条件了)。 Say you have an array for which the ith element is the price of a given stock on day i. Design an algorithm to find the maximum profit. You may complete as many transactions as you like (ie, buy one and sell one share of the stock multiple times) with the following restrictions: Example: 思路: 参考:https://www.cnblogs.com/jdneo/p/5228004.html 这道题可以用动态规划的思路解决。但是一开始想的时候总是抽象不出状态转移方程来,之后看到了一种用状态机的思路,觉得很清晰,特此拿来分享,先看如下状态转移图 s0表示在第i天之前最后一个操作是冷冻期(此时既可以继续休息,又可以开始买入),此时的最大收益。 s1表示在第i天之前最后一个操作是买(此时可以卖出,可以休息),此时的最大收益。 s2表示在第i天之前最后一个操作是卖(此时只能休息),此时的最大收益。 这里我们把状态分成了三个,根据每个状态的指向,我们可以得出下面的状态转移方程: 这样就清晰了很多。 Given a m x n grid filled with non-negative numbers, find a path from top left to bottom right which minimizes the sum of all numbers along its path. Note: You can only move either down or right at any point in time. Example: 思路:这题挺简单的,我们维护一个二维的dp数组,其中dp[i][j]表示当前位置的最小路径和 Given s1, s2, s3, find whether s3 is formed by the interleaving of s1 and s2. Example 1: Example 2: 思路: 只要是遇到字符串的子序列或是匹配问题直接就上动态规划Dynamic Programming,其他的都不要考虑,什么递归呀的都是浮云,千辛万苦的写了递归结果拿到OJ上妥妥Time Limit Exceeded,能把人气昏了,所以还是直接就考虑DP解法省事些。 可以用递归做,每匹配s1或者s2中任意一个就递归下去。但是会超时。 DP设计: s1, s2只有两个字符串,因此可以展平为一个二维地图,判断是否能从左上角走到右下角。 边界条件: 这道题的大前提是字符串s1和s2的长度和必须等于s3的长度,如果不等于,肯定返回false。那么当s1和s2是空串的时候,s3必然是空串,则返回true。所以直接给dp[0][0]赋值true,然后若s1和s2其中的一个为空串的话,那么另一个肯定和s3的长度相等,则按位比较,若相同且上一个位置为True,赋True,其余情况都赋False,这样的二维数组dp的边缘就初始化好了。 递推关系: 在任意非边缘位置dp[i][j]时,s1到达第i个元素,s2到达第j个元素: 它的左边或上边有可能为True或是False,如果左边和右上都是false,则此路不通 否则,判断该位置是否与s3位置匹配 地图上往右一步就是s2[j-1]匹配s3[i+j-1]。 地图上往下一步就是s1[i-1]匹配s3[i+j-1]。 示例:s1="aa",s2="ab",s3="aaba"。标1的为可行。最终返回右下角。 0 a b 0 1 1 0 a 1 1 1 a 1 0 1 Given a string s1, we may represent it as a binary tree by partitioning it to two non-empty substrings recursively(这里分割可以是任意处的分割,而不是二分). Below is one possible representation of s1 = To scramble the string, we may choose any non-leaf node and swap its two children. For example, if we choose the node We say that Similarly, if we continue to swap the children of nodes We say that Given two strings s1 and s2 of the same length, determine if s2 is a scrambled string of s1. Example 1: Example 2: 题意:判断一个字符串是否为另一个字符串“乱序”得到,这种乱序采用的方式是将一个字符串从某个位置“割开”,形成两个子串,然后对两个子串进行同样的“割开”操作,直到到达叶子节点,无法再分割。然后对非叶子节点的左右孩子节点进行交换,最后重新从左至右组合形成新的字符串,由于这个过程中存在字符位置的变化,因此,原来的字符串顺序可能会被打乱,当然也可能没有(同一个非叶子节点的左右孩子交换0次或偶数次,就无变化)。 传统递归时间复杂度太高,这里使用对子串排序,如果两者排序后不相同,直接剪枝,从而降低时间复杂度 A message containing letters from Given a non-empty string containing only digits, determine the total number of ways to decode it. Example 1: Example 2: 思路:这题不难,但是!!!对0的处理很麻烦,老是会漏掉情况,要考虑清楚100,101这类情况 Given a string S and a string T, count the number of distinct subsequences of S which equals T. A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, Example 1: Example 2: 思路:这题我竟然做出来了,总结下主要两个套路: (1)把要求变换的两个字符串写成横竖形式 (2)dp数组里记录的内容就是我们所要求的内容 Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, determine if s can be segmented into a space-separated sequence of one or more dictionary words. Note: Example 1: Example 2: Example 3: 思路:如果直接暴力做,其实很难,因为每次字段都长短起始不一,所以我们用dp数组存放前面的匹配情况,保存中间的计算结果。 我们就用一个一维的dp数组,其中dp[i]表示范围[0, i)内的子串是否可以拆分,注意这里dp数组的长度比s串的长度大1,是因为我们要handle空串的情况,我们初始化dp[0]为true,然后开始遍历。 注意这里我们需要两个for循环来遍历,因为此时已经没有递归函数了,所以我们必须要遍历所有的子串,我们用j把[0, i)范围内的子串分为了两部分,[0, j) 和 [j, i),其中范围 [0, j) 就是dp[j],范围 [j, i) 就是s.substr(j, i-j),其中dp[j]是之前的状态,我们已经算出来了,可以直接取,只需要在字典中查找s.substr(j, i-j)是否存在了,如果二者均为true,将dp[i]赋为true,并且break掉,此时就不需要再用j去分[0, i)范围了,因为[0, i)范围已经可以拆分了。 Given a non-empty string s and a dictionary wordDict containing a list of non-empty words, add spaces in s to construct a sentence where each word is a valid dictionary word. Return all such possible sentences. Note: Example 1: Example 2: Example 3: 思路: 直接用递归会超时,因为举例来说: 如果当s变成 "sanddog"的时候,那么此时我们知道其可以拆分成sand和dog,当某个时候如果我们又遇到了这个 "sanddog"的时候,我们难道还需要再调用递归算一遍吗,当然不希望啦,所以我们要将这个中间结果保存起来,由于我们必须要同时保存s和其所有的拆分的字符串,那么可以使用一个HashMap,来建立二者之间的映射。 字典中保存{ "sanddog":["sand dog"]} 那么在递归函数中 (1) 我们首先检测当前s是否已经有映射,有的话直接返回即可 (2) 如果s为空了,我们如何处理呢,题目中说了给定的s不会为空,但是我们递归函数处理时s是会变空的,这时候我们是直接返回空集吗,这里有个小trick,我们其实放一个空字符串返回,为啥要这么做呢?我们观察题目中的Output,发现单词之间是有空格,而最后一个单词后面没有空格,所以这个空字符串就起到了标记当前单词是最后一个,那么我们就不要再加空格了。 The demons had captured the princess (P) and imprisoned her in the bottom-right corner of a dungeon. The dungeon consists of M x N rooms laid out in a 2D grid. Our valiant knight (K) was initially positioned in the top-left room and must fight his way through the dungeon to rescue the princess. The knight has an initial health point represented by a positive integer. If at any point his health point drops to 0 or below, he dies immediately. Some of the rooms are guarded by demons, so the knight loses health (negative integers) upon entering these rooms; other rooms are either empty (0's) or contain magic orbs that increase the knight's health (positive integers). In order to reach the princess as quickly as possible, the knight decides to move only rightward or downward in each step. Write a function to determine the knight's minimum initial health so that he is able to rescue the princess. For example, given the dungeon below, the initial health of the knight must be at least 7 if he follows the optimal path Note: 思路: 这题看着简单,其实有一个难点:如果从起始位置开始遍历,我们并不知道初始时应该初始化的血量,但是到达公主房间后,我们知道血量至少不能小于1,如果公主房间还需要掉血的话,那么掉血后剩1才能保证起始位置的血量最小。 故这道题应该逆向处理: 最先处理的是公主所在的房间的起始生命值,然后慢慢向第一个房间扩散,不断的得到各个位置的最优的生命值,逆向推正是本题的精髓所在。 dp中存储着该位置到公主所在房间所需的最低血量,如果该血量为负数,则设置成1即可 优化:其实使用一个一维数组覆盖即可 You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed, the only constraint stopping you from robbing each of them is that adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night. Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police. Example 1: Example 2: 思路:最开始写个个直接间隔算的,但是这样是会有问题的,比如[2,1,1,2]这种会有问题 正确应该使用dp记录 到达该位置时最大数,由于不能抢相邻的,所以我们可以用再前面的一个的dp值加上当前的房间值,和当前房间的前面一个dp值比较,取较大值当做当前dp值,所以我们可以得到状态转移方程dp[i] = max(num[i] + dp[i - 2], dp[i - 1]) You are a professional robber planning to rob houses along a street. Each house has a certain amount of money stashed. All houses at this place are arranged in a circle. That means the first house is the neighbor of the last one. Meanwhile, adjacent houses have security system connected and it will automatically contact the police if two adjacent houses were broken into on the same night. Given a list of non-negative integers representing the amount of money of each house, determine the maximum amount of money you can rob tonight without alerting the police. Example 1: Example 2: 思路:相较上一题,这题变成了一个圈,算两次即可,第一次抢劫第一家,最后一家不抢,第二次不抢第一家,最后一家可以抢 The thief has found himself a new place for his thievery again. There is only one entrance to this area, called the "root." Besides the root, each house has one and only one parent house. After a tour, the smart thief realized that "all houses in this place forms a binary tree". It will automatically contact the police if two directly-linked houses were broken into on the same night. Determine the maximum amount of money the thief can rob tonight without alerting the police. Example 1: Example 2: 思路:这题用上面的递归做是不行的,会重复计算,对于下面这种情况无法计算 这种问题是很典型的递归问题,我们可以利用回溯法来做,因为当前的计算需要依赖之前的结果, (1)对于某一个节点,如果其左子节点存在,我们通过递归调用函数,算出不包含左子节点返回的值,同理,如果右子节点存在,算出不包含右子节点返回的值 (2)那么此节点的最大值可能有两种情况,一种是该节点值加上不包含左子节点和右子节点的返回值之和,另一种是左右子节点返回值之和不包含当期节点值,取两者的较大值返回即可 (3)但是这种方法无法通过OJ,超时了,所以我们必须优化这种方法,这种方法重复计算了很多地方,比如要完成一个节点的计算,就得一直找左右子节点计算,我们可以把已经算过的节点用哈希表保存起来,以后递归调用的时候,现在哈希表里找,如果存在直接返回,如果不存在,等计算出来后,保存到哈希表中再返回,这样方便以后再调用 Given an integer array nums, find the sum of the elements between indices i and j (i ≤ j), inclusive. Example: Note: 思路:这题确实简单,使用一个dp数组,存放0-i直接的和即可 Given a 2D matrix matrix, find the sum of the elements inside the rectangle defined by its upper left corner (row1, col1) and lower right corner (row2, col2). Example: Note: 思路:情况比上面复杂一点,建立一个累计区域和的数组,然后根据边界值的加减法来快速求出给定区域之和。 这里我们维护一个二维数组dp,其中dp[i][j]表示累计区间(0, 0)到(i, j)这个矩形区间所有的数字之和,那么此时如果我们想要快速求出(r1, c1)到(r2, c2)的矩形区间时,只需dp[r2][c2] - dp[r2][c1 - 1] - dp[r1 - 1][c2] + dp[r1 - 1][c1 - 1]即可 下面的代码中我们由于用了辅助列和辅助行,所以下标会有些变化,增加一列全0,一行全0,方便计算 We are given A valid permutation is a permutation How many valid permutations are there? Since the answer may be large, return your answer modulo Example 1: Note: 思路: 这题直接dfs暴力是不行的,加上剪枝时间复杂度仍然超级高 思路应该是dp,难点是怎样dp 假如我们现在已经有了一个 "DID" 模式的序列 1032,假如我们还想加一个D,变成 "DIDD",该怎么加数字呢? 多了一个模式符,就多了一个数字4,显然直接加4是不行的,实际是可以在末尾加2的,但是要先把原序列中大于等于2的数字都先加1,即 1032 -> 1043,然后再加2,变成 10432,就是 "DIDD" 了。虽然我们改变了序列的数字顺序,但是升降模式还是保持不变的。同理,也是可以加1的,1032 -> 2043 -> 20431,也是可以加0的,1032 -> 2143 -> 21430。但是无法加3和4,因为 1032 最后一个数字2很很重要,所有小于等于2的数字,都可以加在后面,从而形成降序。那么反过来也是一样,若要加个升序,比如变成 "DIDI",猜也猜的出来,后面要加大于2的数字,然后把所有大于等于这个数字的地方都减1,比如加上3,1032 -> 1042 -> 10423,再比如加上4,1032 -> 1032 -> 10324。 通过上面的分析,我们知道了最后一个位置的数字的大小非常的重要,不管是要新加升序还是降序,最后的数字的大小直接决定了能形成多少个不同的序列,这个就是本题的隐藏信息,所以我们在定义 dp 数组的时候必须要把最后一个数字考虑进去,这样就需要一个二维的 dp 数组,其中 dp[i][j] 表示由范围 [0, i] 内的数字组成且最后一个数字为j的不同序列的个数。 https://www.cnblogs.com/grandyang/p/11094525.html Write a function that takes an unsigned integer and return the number of '1' bits it has (also known as the Hamming weight). Example 1: 思路:这题太简单了。。。 Reverse bits of a given 32 bits unsigned integer. Example 1: Example 2: Note: 思路:注意这里是逆置,不是每个位取反,注意看题。故这题比较简单,把要翻转的数从右向左一位位的取出来(通过n = n & 1取出,n = n >> 1移动),如果取出来的是1,我们将结果res左移一位并且加上1;如果取出来的是0,我们将结果res左移一位,然后将n右移一位即可 All DNA is composed of a series of nucleotides abbreviated as A, C, G, and T, for example: "ACGAATTCCG". When studying DNA, it is sometimes useful to identify repeated sequences within the DNA. Write a function to find all the 10-letter-long sequences (substrings) that occur more than once in a DNA molecule. Example: 思路:找到所有出现2次及以上的字符串,使用自定义的map和hash方法会让算法的效率得到很大的提高 解法二: 使用位运算,速度更快,使用空间更少 构成输入字符串的字符只有四种,分别是A, C, G, T,下面我们来看下它们的ASCII码用二进制来表示: A: 0100 0001 C: 0100 0011 G: 0100 0111 T: 0101 0100 由于我们的目的是利用位来区分字符,当然是越少位越好,通过观察发现,每个字符的后三位都不相同,故而我们可以用末尾三位来区分这四个字符。而题目要求是10个字符长度的串,每个字符用三位来区分,10个字符需要30位,在32位机上也OK。为了提取出后30位,我们还需要用个mask,取值为0x7ffffff,用此mask可取出后27位,再向左平移三位即可。 The gray code is a binary numeral system where two successive values differ in only one bit. Given a non-negative integer n representing the total number of bits in the code, print the sequence of gray code. A gray code sequence must begin with 0. Example 1: Example 2: 思路:格雷码主要特点是两个相邻数的代码只有一位二进制数不同的编码,格雷码的处理主要是位操作 Bit Operation 然后我们来看看其他的解法,参考维基百科上关于格雷码的性质,有一条是说镜面排列的,n位元的格雷码可以从n-1位元的格雷码以上下镜射后加上新位元的方式快速的得到,如下图所示一般。 有了这条性质,我们很容易的写出代码如下: Given a non-empty array of integers, every element appears twice except for one. Find that single one. Note: Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory? Example 1: Example 2: 这题很巧妙,利用计算机按位储存数字的特性来做的,因为每个数如果相同就出现两次,利用异或操作可以变为0,剩下那一个就是只出现一次的。用到的知识是A^A=0,两个相同的数异或变为0,然后0^B=B,这样即可找到出现一次的数。 Given a non-empty array of integers, every element appears three times except for one, which appears exactly once. Find that single one. Note: Your algorithm should have a linear runtime complexity. Could you implement it without using extra memory? Example 1: Example 2: 思路:我们可以建立一个32位的数字,来统计每一位上1出现的个数,我们知道如果某一位上为1的话,那么如果该整数出现了三次,对3去余为0,我们把每个数的对应位都加起来对3取余,最终剩下来的那个数就是单独的数字。 Given an array of numbers Example: Note: 思路:这题的难点是在最后得到ab异或的结果以后,怎样去将ab分开 (1)首先我们先把原数组全部异或起来,那么我们会得到一个数字,这个数字是两个不相同的数字异或的结果 (2)我们取出其中任意一位为‘1’的位,用来后面去区分a,b 就拿题目中的例子来说,如果我们将其全部亦或起来,我们知道相同的两个数亦或的话为0,那么两个1,两个2,都抵消了,就剩3和5亦或起来,那么就是二进制的11和101亦或,得到110。 然后我们先初始化diff为1,如果最右端就是1,那么diff与a_xor_b去做与会得到1,否则是0,我们左移diff,用10再去做与,此时得到结果11,找到最右端第一个1了 (3)用diff来和数组中每个数字相与 根据结果的不同,一定可以把3和5区分开来,而其他的数字由于是成对出现,所以区分开来也是成对的,最终都会亦或成0,不会3和5产生影响。分别将两个小组中的数字都异或起来,就可以得到最终结果了 Given an integer, write a function to determine if it is a power of two. Example 1: Example 2: Example 3: 思路:这道题要注意-2147483648 关于c++ int的表示范围:https://blog.csdn.net/y12345678904/article/details/52854230 我们来观察下2的次方数的二进制写法的特点: 1 2 4 8 16 .... 1 10 100 1000 10000 .... 那么我们很容易看出来2的次方数都只有一个1,剩下的都是0,所以我们的解题思路就有了,我们只要每次判断最低位是否为1,然后向右移位,最后统计1的个数即可判断是否是2的次方数。(一定要判断输入大于0) 解法二: 那么它的二进数必然是最高位为1,其它都为0,那么如果此时我们减1的话,则最高位会降一位,其余为0的位现在都为变为1,那么我们把两数相与,就会得到0 Given an array containing n distinct numbers taken from Example 1: Example 2: Note: 思路: 既然0到n之间少了一个数,我们将这个少了一个数的数组合0到n之间完整的数组异或一下,那么相同的数字都变为0了,剩下的就是少了的那个数字了(异或或者直接加减都可以) Given a string array Example 1: Example 2: Example 3: 思路:题目中说都是小写字母,那么只有26位,一个整型数int有32位,我们可以用后26位来对应26个字母,若为1,说明该对应位置的字母出现过,那么每个单词的都可由一个int数字表示,两个单词没有共同字母的条件是这两个int数相与为0 Given a range [m, n] where 0 <= m <= n <= 2147483647, return the bitwise AND of all numbers in this range, inclusive. Example 1: Example 2: 思路:m到n之间数相与的结果,其实就是m和n左边最长的公共1的部分,如: [5, 7]里共有三个数字,分别写出它们的二进制为: 101 110 111 相与后的结果为100,仔细观察我们可以得出,最后的数是该数字范围内所有的数的左边共同的部分。 如果上面那个例子不太明显,我们再来看一个范围[26, 30],它们的二进制如下: 11010 11011 11100 11101 11110 Given an integer, write a function to determine if it is a power of three. Example 1: Example 2: Example 3: Example 4: Follow up: 思路:这题不能位操作哎,用循环的话就不断去除3 解法二:不用递归来做 利用对数的换底公式来做,高中学过的换底公式为logab = logcb / logca,那么如果n是3的倍数,则log3n一定是整数,我们利用换底公式可以写为log3n = log10n / log103,注意这里一定要用10为底数,不能用自然数或者2为底数,否则当n=243时会出错,原因请看这个帖子。现在问题就变成了判断log10n / log103是否为整数,在c++中判断数字a是否为整数,我们可以用 a - int(a) == 0 来判断
任何跨越中点的子数组都是由两个子数组A[i...mid]和A[mid+1...j]组成,其中low≤i≤midlow≤i≤mid且midclass Solution {
public:
int maxSubArray(vectorMaximum Product Subarray(mid)
nums, find the contiguous subarray within an array (containing at least one number) which has the largest product.Input: [2,3,-2,4]
Output: 6
Explanation: [2,3] has the largest product 6.
Input: [-2,0,-1]
Output: 0
Explanation: The result cannot be 2, because [-2,-1] is not a subarray.class Solution {
public:
int maxProduct(vectorclass Solution {
public:
int maxProduct(vectorLongest Increasing Subsequence(最长递增序列)(mid)
Input:
[10,9,2,5,3,7,101,18]
Output: 4
Explanation: The longest increasing subsequence is [2,3,7,101], therefore the length is 4.
在最开始时,dp[i] = 1代表序列中只含有自身。
本问题的关键在于对于循环和大小关系的确定:我们对于任意的一个i,需要从0~i-1判断每个nums[i],nums[j]的大小关系。从而确定dp[i]的值,通过两者之间的大小关系我们可以得出:
若nums[i] > nums[j],则dp[i] = dp[j]+1
然后对于j从0~i-1,我们对上述式子求最大值,便可得出转移方程如下:
dp[i] = max(dp[i],dp[j]+1)
class Solution {
public:
int lengthOfLIS(vector
我们定义一个序列B[1..9],然后令 i = 1 to 9 逐个考察这个序列。
此外,我们用一个变量Len来记录现在最长算到多少了
首先,把d[1]有序地放到B里,令B[1] = 2,就是说当只有1一个数字2的时候,长度为1的LIS的最小末尾是2。这时Len=1
然后,把d[2]有序地放到B里,令B[1] = 1,就是说长度为1的LIS的最小末尾是1,d[1]=2已经没用了,很容易理解吧。这时Len=1
接着,d[3] = 5,d[3]>B[1],所以令B[1+1]=B[2]=d[3]=5,就是说长度为2的LIS的最小末尾是5,很容易理解吧。这时候B[1..2] = 1, 5,Len=2
再来,d[4] = 3,它正好加在1,5之间,放在1的位置显然不合适,因为1小于3,长度为1的LIS最小末尾应该是1,这样很容易推知,长度为2的LIS最小末尾是3,于是可以把5淘汰掉,这时候B[1..2] = 1, 3,Len = 2
继续,d[5] = 6,它在3后面,因为B[2] = 3, 而6在3后面,于是很容易可以推知B[3] = 6, 这时B[1..3] = 1, 3, 6,还是很容易理解吧? Len = 3 了噢。
第6个, d[6] = 4,你看它在3和6之间,于是我们就可以把6替换掉,得到B[3] = 4。B[1..3] = 1, 3, 4, Len继续等于3
第7个, d[7] = 8,它很大,比4大,嗯。于是B[4] = 8。Len变成4了
第8个, d[8] = 9,得到B[5] = 9,嗯。Len继续增大,到5了。
最后一个, d[9] = 7,它在B[3] = 4和B[4] = 8之间,所以我们知道,最新的B[4] =7,B[1..5] = 1, 3, 4, 7, 9,Len = 5。
于是我们知道了LIS的长度为5。
!!!!! 注意。这个1,3,4,7,9不是LIS,它只是存储的对应长度LIS的最小末尾。有了这个末尾,我们就可以一个一个地插入数据。虽然最后一个d[9] = 7更新进去对于这组数据没有什么意义,但是如果后面再出现两个数字 8 和 9,那么就可以把8更新到d[5], 9更新到d[6],得出LIS的长度为6。
然后应该发现一件事情了:在B中插入数据是有序的,而且是进行替换而不需要挪动——也就是说,我们可以使用二分查找,将每一个数字的插入时间优化到O(logN),于是算法的时间复杂度就降低到了O(NlogN)!class Solution {
public:
int lengthOfLIS(vectorPalindrome Partitioning II(分割回文串)(hard)
Input: "aab"
Output: 1
Explanation: The palindrome partitioning ["aa","b"] could be produced using 1 cut.
class Solution {
public:
int minCut(string s) {
int n = s.size();
if(n == 0) return 0;
vectorMaximal Rectangle(最大矩形)(hard)
Input:
[
["1","0","1","0","0"],
["1","0","1","1","1"],
["1","1","1","1","1"],
["1","0","0","1","0"]
]
Output: 6class Solution {
public:
int maximalRectangle(vectorBest Time to Buy and Sell Stock III(hard)
Input: [3,3,5,0,0,3,1,4]
Output: 6
Explanation: Buy on day 4 (price = 0) and sell on day 6 (price = 3), profit = 3-0 = 3.
Then buy on day 7 (price = 1) and sell on day 8 (price = 4), profit = 4-1 = 3.Input: [1,2,3,4,5]
Output: 4
Explanation: Buy on day 1 (price = 1) and sell on day 5 (price = 5), profit = 5-1 = 4.
Note that you cannot buy on day 1, buy on day 2 and sell them later, as you are
engaging multiple transactions at the same time. You must sell before buying again.
Input: [7,6,4,3,1]
Output: 0
Explanation: In this case, no transaction is done, i.e. max profit = 0.class Solution {
public:
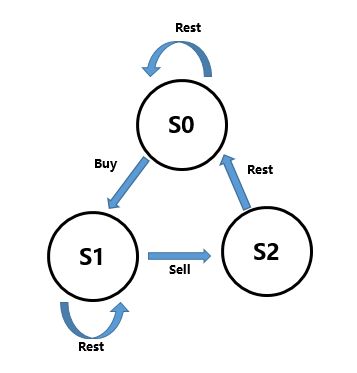
int maxProfit(vectorBest Time to Buy and Sell Stock with Cooldown(hard)
Input: [1,2,3,0,2]
Output: 3
Explanation: transactions = [buy, sell, cooldown, buy, sell]
class Solution {
public:
int maxProfit(vectorMinimum Path Sum(mid)
Input:
[
[1,3,1],
[1,5,1],
[4,2,1]
]
Output: 7
Explanation: Because the path 1→3→1→1→1 minimizes the sum.class Solution {
public:
int minPathSum(vectorInterleaving String(hard)
Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbcbcac"
Output: true
Input: s1 = "aabcc", s2 = "dbbca", s3 = "aadbbbaccc"
Output: falseclass Solution {
public:
bool isInterleave(string s1, string s2, string s3) {
int n1 = s1.size(),n2 = s2.size(),n3 = s3.size();
// 长度判断
if(n1+n2 != n3) return false;
if(n1 == 0) return s2 == s3;
if(n2 == 0) return s1 == s3;
vectorScramble String
"great": great
/ \
gr eat
/ \ / \
g r e at
/ \
a t
"gr" and swap its two children, it produces a scrambled string "rgeat". rgeat
/ \
rg eat
/ \ / \
r g e at
/ \
a t
"rgeat" is a scrambled string of "great"."eat" and "at", it produces a scrambled string "rgtae". rgtae
/ \
rg tae
/ \ / \
r g ta e
/ \
t a
"rgtae" is a scrambled string of "great".Input: s1 = "great", s2 = "rgeat"
Output: true
Input: s1 = "abcde", s2 = "caebd"
Output: false
思路1:递归加上剪枝class Solution {
public:
bool isScramble(string s1, string s2) {
int m = s1.size(),n = s2.size();
if(m != n) return false;
if(s1 == s2) return true;
// 使用排序剪枝
string str1 = s1,str2 = s2;
sort(str1.begin(),str1.end());
sort(str2.begin(),str2.end());
if(str1 != str2) return false;
// 递归
for(int i = 1;i < m;i++){
if(isScramble(s1.substr(0,i),s2.substr(0,i)) && isScramble(s1.substr(i,m-i),s2.substr(i,m-i)))
return true;
if(isScramble(s1.substr(0,i),s2.substr(m-i)) && isScramble(s1.substr(i),s2.substr(0,m-i)))
return true;
}
return false;
}
};Decode Ways(mid)
A-Z is being encoded to numbers using the following mapping:'A' -> 1
'B' -> 2
...
'Z' -> 26
Input: "12"
Output: 2
Explanation: It could be decoded as "AB" (1 2) or "L" (12).
Input: "226"
Output: 3
Explanation: It could be decoded as "BZ" (2 26), "VF" (22 6), or "BBF" (2 2 6).class Solution {
public:
int numDecodings(string s) {
if(s.empty()) return 0;
if(s[0] == '0') return 0;
int n = s.size(),front = s[0]-'0';
vectorDistinct Subsequences(hard)
"ACE" is a subsequence of "ABCDE" while "AEC" is not).Input: S =
"rabbbit", T = "rabbit"
Output: 3
Explanation:
As shown below, there are 3 ways you can generate "rabbit" from S.
(The caret symbol ^ means the chosen letters)
rabbbit
^^^^ ^^
rabbbit
^^ ^^^^
rabbbit
^^^ ^^^
Input: S =
"babgbag", T = "bag"
Output: 5
Explanation:
As shown below, there are 5 ways you can generate "bag" from S.
(The caret symbol ^ means the chosen letters)
babgbag
^^ ^
babgbag
^^ ^
babgbag
^ ^^
babgbag
^ ^^
babgbag
^^^class Solution {
public:
long long numDistinct(string s, string t) {
int m = s.size(),n = t.size();
if(m <= n) return s==t;
vectorWord Break(mid)
Input: s = "leetcode", wordDict = ["leet", "code"]
Output: true
Explanation: Return true because "leetcode" can be segmented as "leet code".Input: s = "applepenapple", wordDict = ["apple", "pen"]
Output: true
Explanation: Return true because "applepenapple" can be segmented as "apple pen apple".
Note that you are allowed to reuse a dictionary word.
Input: s = "catsandog", wordDict = ["cats", "dog", "sand", "and", "cat"]
Output: falseclass Solution {
public:
bool wordBreak(string s, vectorWord Break II(hard)
Input:
s = "
catsanddog"
wordDict = ["cat", "cats", "and", "sand", "dog"]
Output:
[
"cats and dog",
"cat sand dog"
]
Input:
s = "pineapplepenapple"
wordDict = ["apple", "pen", "applepen", "pine", "pineapple"]
Output:
[
"pine apple pen apple",
"pineapple pen apple",
"pine applepen apple"
]
Explanation: Note that you are allowed to reuse a dictionary word.
Input:
s = "catsandog"
wordDict = ["cats", "dog", "sand", "and", "cat"]
Output:
[]class Solution {
public:
vectorDungeon Game
RIGHT-> RIGHT -> DOWN -> DOWN.
-2 (K)
-3
3
-5
-10
1
10
30
-5 (P)
class Solution {
public:
int calculateMinimumHP(vectorclass Solution {
public:
int calculateMinimumHP(vectorHouse Robber(打家劫舍)(easy)
Input: [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.Input: [2,7,9,3,1]
Output: 12
Explanation: Rob house 1 (money = 2), rob house 3 (money = 9) and rob house 5 (money = 1).
Total amount you can rob = 2 + 9 + 1 = 12.class Solution {
public:
int rob(vectorHouse Robber II(mid)
Input: [2,3,2]
Output: 3
Explanation: You cannot rob house 1 (money = 2) and then rob house 3 (money = 2),
because they are adjacent houses.
Input: [1,2,3,1]
Output: 4
Explanation: Rob house 1 (money = 1) and then rob house 3 (money = 3).
Total amount you can rob = 1 + 3 = 4.class Solution {
public:
int rob(vectorHouse Robber III(hard)
Input: [3,2,3,null,3,null,1]
3
/ \
2 3
\ \
3 1
Output: 7
Explanation: Maximum amount of money the thief can rob = 3 + 3 + 1 = 7.Input: [3,4,5,1,3,null,1]
3
/ \
4 5
/ \ \
1 3 1
Output: 9
Explanation: Maximum amount of money the thief can rob = 4 + 5 = 9.
3
/ \
14 5
/ \ \
1 3 16
/**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
* };
*/
class Solution {
public:
int rob(TreeNode* root) {
if(!root) return 0;
unordered_mapRange Sum Query - Immutable(easy)
Given nums = [-2, 0, 3, -5, 2, -1]
sumRange(0, 2) -> 1
sumRange(2, 5) -> -1
sumRange(0, 5) -> -3
class NumArray {
public:
NumArray(vectorrange Sum Query 2D - Immutable(medium)

The above rectangle (with the red border) is defined by (row1, col1) = (2, 1) and (row2, col2) = (4, 3), which contains sum = 8.Given matrix = [
[3, 0, 1, 4, 2],
[5, 6, 3, 2, 1],
[1, 2, 0, 1, 5],
[4, 1, 0, 1, 7],
[1, 0, 3, 0, 5]
]
sumRegion(2, 1, 4, 3) -> 8
sumRegion(1, 1, 2, 2) -> 11
sumRegion(1, 2, 2, 4) -> 12
class NumMatrix {
public:
NumMatrix(vectorValid Permutations for DI Sequence(递增递减数列个数)(hard)
S, a length n string of characters from the set {'D', 'I'}. (These letters stand for "decreasing" and "increasing".)P[0], P[1], ..., P[n] of integers {0, 1, ..., n}, such that for all i:
S[i] == 'D', then P[i] > P[i+1], and;S[i] == 'I', then P[i] < P[i+1].10^9 + 7.Input: "DID"
Output: 5
Explanation:
The 5 valid permutations of (0, 1, 2, 3) are:
(1, 0, 3, 2)
(2, 0, 3, 1)
(2, 1, 3, 0)
(3, 0, 2, 1)
(3, 1, 2, 0)
1 <= S.length <= 200S consists only of characters from the set {'D', 'I'}.class Solution:
def numPermsDISequence(self, S: str) -> int:
mod = 1e9+7
n = len(S)
res = 0
dp = [[0]*(n+1) for _ in range(n+1)]
dp[0][0] = 1
for i in range(1,n+1):
if S[i-1] == 'D':
# 递减,新结尾最大是i-1,范围[0,i-1]
for j in range(0,i):
# 上一个串结尾,至少是j,将前面的串的数大于等于j的都+1
for k in range(j,i):
dp[i][j] = (dp[i][j] + dp[i-1][k])%mod
else:
# 递增,新结尾至少是1,[1,i]
for j in range(1,i+1):
# 上一个串结尾,至多是j-1,将前面的串的数大于等于j的都+1
for k in range(0,j):
dp[i][j] = (dp[i][j] + dp[i-1][k])%mod
res = sum(dp[n])%mod
return int(res)位操作
Number of 1 Bits(easy)
Input: 00000000000000000000000000001011
Output: 3
Explanation: The input binary string
00000000000000000000000000001011 has a total of three '1' bits.class Solution {
public:
int hammingWeight(uint32_t n) {
int cnt = 0;
for(int i = 0;i < 32;i++){
if(n & 1 == 1) cnt++;
n = n >> 1;
}
return cnt;
}
};Reverse Bits(easy)
Input: 00000010100101000001111010011100
Output: 00111001011110000010100101000000
Explanation: The input binary string 00000010100101000001111010011100 represents the unsigned integer 43261596, so return 964176192 which its binary representation is 00111001011110000010100101000000.
Input: 11111111111111111111111111111101
Output: 10111111111111111111111111111111
Explanation: The input binary string 11111111111111111111111111111101 represents the unsigned integer 4294967293, so return 3221225471 which its binary representation is 10101111110010110010011101101001.
-3 and the output represents the signed integer -1073741825.class Solution {
public:
uint32_t reverseBits(uint32_t n) {
uint32_t res = 0;
for(int i = 0;i < 32;i++){
if(n & 1 == 1) res = (res << 1) + 1;
else res = res << 1;
n = n >> 1;
}
return res;
}
};Repeated DNA Sequences(medium)
Input: s = "AAAAACCCCCAAAAACCCCCCAAAAAGGGTTT"
Output: ["AAAAACCCCC", "CCCCCAAAAA"]class Solution {
public:
vectorclass Solution {
public:
vectorGray Code
Input: 2
Output:
[0,1,3,2]
Explanation:
00 - 0
01 - 1
11 - 3
10 - 2
For a given n, a gray code sequence may not be uniquely defined.
For example, [0,2,3,1] is also a valid gray code sequence.
00 - 0
10 - 2
11 - 3
01 - 1
Input: 0
Output:
[0]
Explanation: We define the gray code sequence to begin with 0.
A gray code sequence of n has size = 2n, which for n = 0 the size is 20 = 1.
Therefore, for n = 0 the gray code sequence is [0].class Solution {
public:
vectorSingle Number(easy)
Input: [2,2,1]
Output: 1
Input: [4,1,2,1,2]
Output: 4class Solution {
public:
int singleNumber(vectorSingle Number II(mid)
Input: [2,2,3,2]
Output: 3
Input: [0,1,0,1,0,1,99]
Output: 99class Solution {
public:
int singleNumber(vectorSingle Number III(mid)
nums, in which exactly two elements appear only once and all the other elements appear exactly twice. Find the two elements that appear only once.Input:
[1,2,1,3,2,5]
Output: [3,5]
[5, 3] is also correct.class Solution {
public:
vectorPower of Two
Input: 1
Output: true
Explanation: 20 = 1
Input: 16
Output: true
Explanation: 24 = 16Input: 218
Output: falseclass Solution {
public:
bool isPowerOfTwo(int n) {
int cnt = 0;
while(n > 0){
if(n & 1) cnt++;
n = n >> 1;
}
if(cnt == 1) return true;
else return false;
}
};class Solution {
public:
bool isPowerOfTwo(int n) {
return (n > 0) && (!(n & (n-1)));
}
};Missing Number(easy)
0, 1, 2, ..., n, find the one that is missing from the array.Input: [3,0,1]
Output: 2
Input: [9,6,4,2,3,5,7,0,1]
Output: 8
Your algorithm should run in linear runtime complexity. Could you implement it using only constant extra space complexity?class Solution {
public:
int missingNumber(vectorMaximum Product of Word Lengths(mid)
words, find the maximum value of length(word[i]) * length(word[j]) where the two words do not share common letters. You may assume that each word will contain only lower case letters. If no such two words exist, return 0.Input:
["abcw","baz","foo","bar","xtfn","abcdef"]
Output: 16
Explanation: The two words can be "abcw", "xtfn".Input:
["a","ab","abc","d","cd","bcd","abcd"]
Output: 4
Explanation: The two words can be "ab", "cd".Input:
["a","aa","aaa","aaaa"]
Output: 0
Explanation: No such pair of words.class Solution {
public:
int maxProduct(vectorBitwise AND of Numbers Range
Input: [5,7]
Output: 4
Input: [0,1]
Output: 0class Solution {
public:
int rangeBitwiseAnd(int m, int n) {
int i = 0;
while(m != n){
m = m >> 1;
n = n >> 1;
i++;
}
return m << i;
}
};Power of Three(easy)
Input: 27
Output: true
Input: 0
Output: falseInput: 9
Output: trueInput: 45
Output: false
Could you do it without using any loop / recursion?class Solution {
public:
bool isPowerOfThree(int n) {
while(n && n % 3==0) n = n/3;
return n == 1;
}
};class Solution {
public:
bool isPowerOfThree(int n) {
// 判断int(log10(n) / log10(3)) - log10(n) / log10(3)是否为0,即可判断n是否为3的power
return (n > 0 && int(log10(n) / log10(3)) - log10(n) / log10(3) == 0);
}
};补充一下基础位操作:
判断一个二进制数中是否存在两个连续的1
bool is_true(int n){
return (n & n >> 1) > 0;
};快速统计二进制中1的个数
def my_function(int n){
int count = 0;
while (num)
{
num = num&(num - 1);
count++;
}
return count;
}