java 数组求和_树状数组：萌新的个人理解（1）
归航return：树状数组：萌新的个人理解（0）zhuanlan.zhihu.com
![]()
![]()
，修改某个位置的数的时间复杂度是
![]()
。如果使用数组大小的平方根作为分块大小，那么查询前缀和的时间复杂度是
![]()
，修改某个位置的数的时间复杂度是
![]()
。但是事实上，有一种针对此类单点查询和修改更快的数据结构，这就是：树状数组。
图源：OI Wiki（即上方超链接）
![]()
。（不考虑整数溢出问题）
![]()
上的数组和可以拆分成
![]()
和
![]()
上的和。
![]()
![]()
的二进制表示是这样的：
![]()
![]()
都是降序排列的。例如，当
![]()
的时候，因为
![]()
，因此
![]()
，
![]()
。那么在上述基础上，我们就可以将计算
![]()
个长度均为 2 的幂的子区间的和的求和问题。也就是说：
![]()
![]()
的结果。很容易知道，上述公式
![]()
中，我们最多要计算
![]()
个求和的表达式。以
![]()
为例，那么就有：
![]()
。
![]()
是降序排列的，因此我们发现，上述每个区间的右端点的
![]()
。
![]()
![]()
是一个解，因为只要
![]()
是一个正整数，就必然有
![]()
。定义迭代：
![]()
，规定
![]()
。
![]()
。由上面的
![]()
为奇数的情况，若不然，只需要使用
![]()
代替
![]()
即可转化为这种情况。此时有：
![]()
，
![]()
，于是我们只需证明：
![]()
即可。显然，由于
![]()
是偶数，那么必然有
![]()
，于是这就证明完毕了。 定义
![]()
，
![]()
，根据上述结论就可以得到：
![]()
![]()
中都包含了对下标为
![]()
的求和情况，需要相应加上对
![]()
的修改情况。任何一个大于
![]()
的下标
![]()
，且不是上述
![]()
中的下标，一定存在一个非负整数
![]()
，使得
![]()
。此时必然有
![]()
是偶数，否则这个区间内不存在
![]()
。我们来证明：
![]()
。
![]()
。若不然，这意味着
![]()
对应的位遭到了修改，因而这个时候一定有
![]()
，这是不符合要求的。
![]()
和更高的二进制位，都不会发生变动，因此的确有
![]()
，也就意味着
![]()
，因此其他的下标都不符合要求。
![]()
的方法，不过我为了让代码看起来更简单，使用的是 trivial 的时间复杂度是
![]()
的方法进行构造过程。
![]()
范围内所有元素的和，也就是原来数组下标中
![]()
内的求和结果，也就是
![]()
的结果，不难想到，如果
![]()
和
![]()
范围内的求和结果相减，自然也就得到了
![]()
范围内的求和结果。
![]()
。代码如下：
![]()
，但由于实际的常数问题（
回顾
在上一部分中，我们回顾了经典的前缀和问题的思路，包括在最平凡的前缀和思想和使用平方根作为分块大小的思想。使用最平凡的前缀和思想，查询前缀和的时间复杂度是
引理
- 可以使用以下函数获取一个整数的二进制表示中的最低的 1 对应的位置：
int lowBit(int x){
if (x == INT_MIN){
return INT_MIN;
}
return x & (-x);
}//C++，if you use Java, you should use Integer.MIN_VALUE instead.
证明如下：如果输入的整数是 INT_MIN，它的二进制表示是 0x80000000，正好最高位就是一个 1，因此返回本身就是最低的 1 对应的位置；如果输入的整数是 0，它的二进制表示是 0x00000000，一个 0 都没有，返回结果也正好是 0，是自洽的。
在其他的情况下：注意到：-x 这个运算在二进制上的本质是首先将原始数据逐个取反，最后加上 1。因此，如果这个整数的二进制表示结尾是 1，那么我们可以想像，反转之后再加上 1，只有最后一位的那个数字才是 1，其他的结果都被反转了，因此这个时候正好就应该返回的是 1。假设这个数字的二进制表示有若干个 0 结尾，例如：10000，那么反转之后再加上 1，正好可以进位，使得最后一个 1 对应的位置还是 1，而这个位置前面的相与的性质和前一种情况类似，因此也只有这个位置上的 1 保留下来。
综上所述，这个函数是正确的。
2.lowBit 函数的基本性质：
只需要简单地使用位运算左移的思想就可以理解这个结果。
3. 任何一个下标范围闭区间
这个只需要使用简单的求和公式即可验证，这是显然的。
基本思想
首先，暂时约定数组的下标从 1 开始，然后在最后代码实现的时候，我们再将其还原到从 0 开始。
任何一个正整数都可以借助其二进制表示，表示成若干个二的非负整数次幂之和。根据前缀和的基本思路，只要我们能求出这个数组中从开始的位置（也就是 a[1] ）到给定位置（也就是 a[n]）的和，那么其他的情况也就都解决了。假设
WLOG，规定上述的
a[1] 到 a[n] 的和的过程，拆分成
最后一个地方是 n 是因为这个地方正好就的确是
由于我们规定
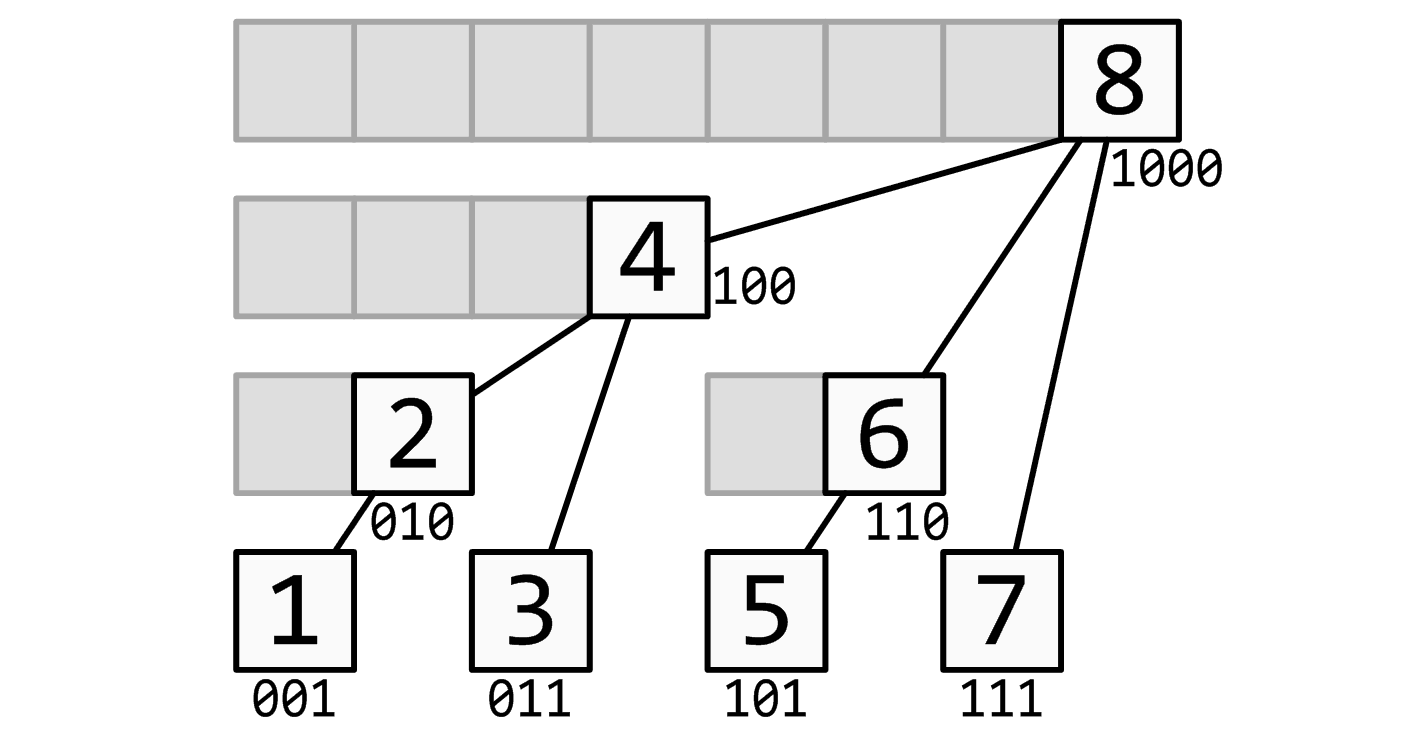
lowBit 函数，正好就是这个区间内包含的整数的个数（也就是右端点减去左端点然后加上 1，这个 1 千万不能忘记，这属于典型的 off-by-one-error）。因此，如果我们维护一个额外数组 assist（下标仍然从 1 开始），规定 assist[i] 代表的是 [i-lowBit(i)+1, i] 上区间的和，那么我们便可以使用循环迭代的方法，得到 [1, i] 范围内的前缀和。下面是 C++ 风格的伪代码——因为数组下标并不是从 1 开始。
int getSum(const vector& arr, int idx){
int ans = 0;
while (idx > 0){
ans += arr[idx];
idx -= lowBit(idx);
}
return ans;
}//C++ style pseudocode, cause the index in real std::vector starts from 0.
这就完成了求和的过程，时间复杂度是
对于动态维护前缀和的问题，我们不仅关心的是求和问题，更关心的是单点修改问题，假设修改的下标是 x，其中下标仍然暂时规定从 1 开始，修改的差值为 diff。那么，哪些下标对应的求和在上述范围内呢？我们已经指出，下标为 y 的 assist 数组，对应的是原始数组中：[y-lowBit(y)+1, y]范围内的求和，那么这里实际上就需要解一个不等式：
显然，
我们来证明：
lowBit 函数的基本性质可以知道，WLOG，我们只需考虑当
于是这些
a[x] 的修改值 diff。
下面还要证明，只有这样的下标才包含了针对下标为
首先：
那么，在这种情况下，无论如何运行，
综上所述，我们得到了更新的伪代码如下：
void update(vector& arr, int idx, int diff){
while (idx <= arr.size()){
arr[idx] += diff;
idx += lowBit(idx);
}
}//C++ style pseudocode, cause the index in real std::vector starts from 0.
具体实现
在上述的解释中，我们证明了树状数组的实现原理，接下来让我们具体来实现这个数据结构。
C++ 代码如下：
#include
using namespace std;
class BinaryIndexTree{
private:
vector prefixSumArr;
static int lowBit(int x){
if (x == INT_MIN){
return INT_MIN;
}
return x & (-x);
}
public:
BinaryIndexTree(const vector& arr){
prefixSumArr = vector(arr.size()+1);
for (int i = 0; i < arr.size(); ++i){
add(i, arr[i]);
}
}
void add(int idx, int diff){
++idx;
while (idx < prefixSumArr.size()){
prefixSumArr[idx] += diff;
idx += lowBit(idx);
}
}
int getSum(int left, int right){
return getSum(right)-getSum(left);
}
int getSum(int idx){
int ans = 0;
while (idx > 0){
ans += prefixSumArr[idx];
idx -= lowBit(idx);
}
return ans;
}
};
Java 代码如下：
import java.util.*;
class PrefixSumSupport{
public static int lowBit(int x){
return x & (-x);
}
public static long lowBit(long x){
return x & (-x);
}
}
class BinaryIndexTree {
private int[] prefixSum;
private int length;
private int[] arr;
public BinaryIndexTree(final int[] arr){
resetArr(arr);
}
public BinaryIndexTree(){
this(new int[0]);
}
public BinaryIndexTree(final ArrayList _arr){
resetArr(_arr.stream().mapToInt(i -> i).toArray());
}
public void modify(int idx, int diff){
checkBoundary(idx, length);
arr[idx++] += diff;
while (idx <= length){
prefixSum[idx] += diff;
idx += PrefixSumSupport.lowBit(idx);
}
}
public int returnSum(int begin, int end){
if (begin > end){
throw new IllegalStateException();
}
checkBoundary(begin, length+1);
checkBoundary(end, length+1);
if (begin == end){
return 0;
}
return returnSum(end)-returnSum(begin);
}
private int returnSum(int idx){
int ret = 0;
while (idx > 0){
ret += prefixSum[idx];
idx -= PrefixSumSupport.lowBit(idx);
}
return ret;
}
public void showArr(){
System.out.println(Arrays.toString(arr));
}
public void showPrefix(){
System.out.println(Arrays.toString(prefixSum));
}
public int[] getPrefixSum(){
return Arrays.copyOf(prefixSum, length+1);
}
public int[] getArr(){
return Arrays.copyOf(arr, length);
}
public void resetArr(final int[] arr){
length = arr.length;
prefixSum = new int[arr.length+1];
this.arr = new int[length];
for (int i = 0; i < length; ++i){
modify(i, arr[i]);
}
}
private void checkBoundary(int parameter, int limit){
if (parameter < 0 || parameter >= limit){
throw new ArrayIndexOutOfBoundsException(String.format("Your input is %d, which is out of the limit %dn", parameter, limit));
}
}
@Override
public String toString(){
StringBuffer SB = new StringBuffer();
SB.append("Original array: ");
SB.append(Arrays.toString(arr));
SB.append("n");
SB.append("Prefix sum array: ");
SB.append(Arrays.toString(prefixSum));
return SB.toString();
}
} 本质上是一样的，只不过 Java 多了更多的边界检查。接下来简要解释函数的原理，以 C++ 版本为例：
构造函数 BinaryIndexTree(const vector& arr)
按照惯例，通常前缀和数组的长度，设定为输入数组的长度 +1，能大幅简化问题的边界细节，这里也不例外，分配好空间之后，就将元素逐个逐个加入到树状数组中，这里实际上有一种时间复杂度
修改函数 void add(int idx, int diff)
树状数组中，数组下标的定义被规定从 1 开始，因此这里我们需要首先做一个偏移量，令其 +1，然后才能使用伪代码里面提到的方法来修改所有波及到的下标之处。
查询求和函数 int getSum(int left, int right) 和 int getSum(int idx)
这里的查询函数，都是左闭右开区间形式的定义，其中第二个函数相当于 left = 0, right = idx 的情况。这里使用左闭右开区间，能让边界条件的处理变得十分自然。 getSum(int idx) 函数，求出来的是转换下标之后
idx == 0，这个时候正好就是自然地定义为结果是 0 了。那么将
离散化
在 LeetCode 中，如果一个题目需要用到树状数组，那么还通常需要利用离散化的思想方法，就是将数组中的元素排序，然后去重。这个动作可以简单地使用一个哈希表和一个排序函数即可完成，时间复杂度为
template
vector discretization(const vector& input){
unordered_set duplicationRemoval(input.begin(), input.end());
vector output(duplicationRemoval.begin(), duplicationRemoval.end());
sort(output.begin(), output.end());
return output;
}
针对非 C++ 语言，上述代码已经足够。但是由于 unordered_set 自带大常数，因此如果是 C++，还可以使用 C++ 标准算法库 std::unique 函数，文档在
这个操作的时间复杂度仍然是
unordered_set 自带大常数，上文已经提及到了），这个算法是跑起来快了不少。一个简单的 unique 函数的 Java 实现：
class MySTLAlgorithmToJava{
public static int unique(int[] arr, int from, int to){
if (from == to){
return from;
}
int ans = from;
while (++from != to){
if (!(arr[ans] == arr[from])){
arr[++ans] = arr[from];
}
}
return ++ans;
}
} 使用 unique 函数之后，代码可以变成这样：
template
vector discretization(const vector& input){
vector output(input);
sort(output.begin(), output.end());
auto it = unique(output.begin(), output.end());
output.erase(it, output.end());
return output;
}
如果要求输入和输出数组类型不同，那么代码可以这样：
template
vector discretization(const vector& input, const outputType& typeIndicator){
vector output(input.begin(), input.end());
sort(output.begin(), output.end());
auto it = unique(output.begin(), output.end());
output.erase(it, output.end());
return output;
}
几道例题
LeetCode 307
307. 区域和检索 - 数组可修改 - 力扣（LeetCode）leetcode-cn.com直接应用上述模版即可。Java 代码如下：
class PrefixSumSupport{...}
class BinaryIndexTree {...}
class NumArray {
BinaryIndexTree Solution;
int[] numsCopy;
public NumArray(int[] nums) {
Solution = new BinaryIndexTree(nums);
numsCopy = Arrays.copyOf(nums, nums.length);
}
public void update(int i, int val) {
int diff = val-numsCopy[i];
numsCopy[i] = val;
Solution.modify(i, diff);
}
public int sumRange(int i, int j) {
int ret = Solution.returnSum(i, j+1);
return ret;
}
}省略号内容直接复制上述 Java 实现即可。
LeetCode 315
315. 计算右侧小于当前元素的个数 - 力扣（LeetCode）leetcode-cn.com逆序数问题。C++ 代码如下：
class BinaryIndexTree{...};
class Solution {
public:
vector countSmaller(vector& nums) {
if (nums.size() == 0){
return {};
}
vector discretization = discrete(nums);
vector ans(nums.size(), 0);
BinaryIndexTree Helper(vector(discretization.size()));
for (int i = nums.size()-1; i >= 0; --i){
int thisIdx = lower_bound(discretization.begin(), discretization.end(), nums[i])-discretization.begin();
ans[i] = Helper.getSum(thisIdx);
//because we want to get count of existence less than current number,
//so thisIdx is literally correct, if the problem is no more than,
//line 12 should be replaced by calling upper_bound function in
Helper.add(thisIdx, 1);
}
return ans;
}
private:
vector discrete(const vector& input){
unordered_set duplicationRemoval;
for (const auto & x : input){
duplicationRemoval.insert(x);
}
vector output;
output.reserve(duplicationRemoval.size());
for (const auto & x : duplicationRemoval){
output.emplace_back(x);
}
sort(output.begin(), output.end());
return output;
}
};
LeetCode 327
327. 区间和的个数 - 力扣（LeetCode）leetcode-cn.com这里因为需要知道的是给定区间范围内的前缀和结果求和，而且是闭区间上的结果，因此为了转换成左闭右开区间，求和的下界我们应该使用 lower_bound 函数，而上界应当使用 upper_bound 函数求解。另外，这个题目如果直接使用 int 类型，会溢出，改成 long 才行。
class BinaryIndexTree{
private:
vector prefixSumArr;
static int lowBit(int x){
if (x == INT_MIN){
return INT_MIN;
}
return x & (-x);
}
public:
BinaryIndexTree(const vector& arr){
prefixSumArr = vector(arr.size()+1);
for (int i = 0; i < arr.size(); ++i){
add(i, arr[i]);
}
}
void add(int idx, int diff){
++idx;
while (idx < prefixSumArr.size()){
prefixSumArr[idx] += diff;
idx += lowBit(idx);
}
}
long getSum(int left, int right){
return getSum(right)-getSum(left);
}
long getSum(int idx){
long ans = 0;
while (idx > 0){
ans += prefixSumArr[idx];
idx -= lowBit(idx);
}
return ans;
}
};
class Solution {
public:
int countRangeSum(vector& nums, int lower, int upper) {
if (nums.size() == 0){
return 0;
}
vector prefixSum = prefixSumGeneration(nums);
vector discreted = discretization(prefixSum);
BinaryIndexTree Helper(vector(discreted.size()));
int ans = 0;
for (int i = 0; i < prefixSum.size(); ++i){
long curSum = prefixSum[i];
int curIdx = lower_bound(discreted.begin(), discreted.end(), curSum)-discreted.begin();
int begin = lower_bound(discreted.begin(), discreted.end(), curSum-upper)-discreted.begin();
int end = upper_bound(discreted.begin(), discreted.end(), curSum-lower)-discreted.begin();
ans += Helper.getSum(begin, end);
Helper.add(curIdx, 1);
}
return ans;
}
private:
vector prefixSumGeneration(const vector& input){
vector output(input.size()+1);
for (int i = 0; i < input.size(); ++i){
output[i+1] = output[i]+input[i];
}
return output;
}
template
vector discretization(const vector& input){
unordered_set duplicationRemoval;
for (const auto & x : input){
duplicationRemoval.insert(x);
}
vector output;
output.reserve(duplicationRemoval.size());
for (const auto & x : duplicationRemoval){
output.emplace_back(x);
}
sort(output.begin(), output.end());
return output;
}
};
LeetCode 493
493. 翻转对 - 力扣（LeetCode）leetcode-cn.com同样需要注意 int 溢出问题。
class BinaryIndexTree{...
};
class Solution {
public:
int reversePairs(vector& nums) {
if (nums.size() <= 1){
return 0;
}
vectordiscreted = discretization(nums);
int ans = 0;
BinaryIndexTree Helper(vector(nums.size()));
for (int i = 0; i < nums.size(); ++i){
int thisIdx = lower_bound(discreted.begin(), discreted.end(), 1L*nums[i])-discreted.begin();
int targetIdx = upper_bound(discreted.begin(), discreted.end(), 2L*nums[i])-discreted.begin();
ans += Helper.getSum(targetIdx, discreted.size());
Helper.add(thisIdx, 1);
}
return ans;
}
private:
vector discretization(const vector& input){
unordered_set removalDuplicate;
for (auto x : input){
removalDuplicate.insert(x);
}
vector output;
for (int x : removalDuplicate){
output.emplace_back(x);
}
sort(output.begin(), output.end());
return output;
}
};
总之，在给定区间范围内的二分求范围，如果左边是闭区间，那么就用 lower_bound 函数，否则用 upper_bound 函数作为左闭右开区间的下界。如果右边是闭区间，就用 upper_bound 函数作为左闭右开区间的上界，否则就是 lower_bound ，这样可以保证我们可以方便地调用库函数，我用 Java 刷题的时候也自己写了一个类似的二分查找库，原封不动地实现了 STL 这几个二分函数，也同样支持泛型数组，自定义比较器的使用。
其他语言的实现：
Javascript：
windliang：二叉索引树（树状数组）的原理zhuanlan.zhihu.com
拓展
我们在查询求和的过程中，将下标拆分成若干个二进制的表示，使用的是 lowBit 函数，那么很容易对偶地猜测，highBit——也就是返回二进制最高位的 1 的函数，是否能对偶地实现同样的功能呢？经过我的思考，发现不是很可行，因为这么做之后，会让修改过程的时间复杂度变得不可接受，具体证明留做习题。
EOF。