菜鸟一个,说的不好还望指点
去年学的树状数组,现在都忘没了,复习一下。
给你一组数据,例如a[1],a[2],a[3],...a[k],..a[n],求任意一段区间和(比如说从a[i]---a[j]的所有数的和),线性求解,时间复杂度O(n),规模较大时,会TLE。怎么办?思路:以空间换时间。提前存储一些数据的和。怎么存储会节省时间?
方法一:构造一个和数组sum,每次输入第i个数据,就计算一下前i个数的和sum[i]。当求取前i个数和时,直接输出sum[i],O(1)时间复杂度,不很好吗。可是。。。如果我想更新一下第j个数据,那么就得连带着更新sum[j],sum[j+1],...sum[n],时间复杂度又是O(n),悲剧。。。
方法其他:还有其他方法,大家自己想吧,也可以查查。
现在隆重推出重量级方法:树状数组。让求和 和更新都是lg(n)。它的奥妙在哪呢?
设这个数组为tree[n](没错,就一个数组)
奥妙一:tree中存着神马东西?
举个栗子:tree[12]
解:12------>1100(把12转换为二进制)
把1100变身------>1001 1010 1011 1100
tree[1100]=a[1001]+a[1010]+a[1011]+a[1100]
也就是tree[12]=a[9]+a[10]+a[11]+a[12]
也就是1100从右向左数第一个1,把1及1后边的0去掉(把100去掉),让a[1001]一直加到a[1100]
再举个复杂点儿的栗子:tree[40]
解:40------>101000
101000变身-------->100001 100010 ... 101000
tree[101000]=a[100001]+a[100010]+...+a[101000]
也就是tree[40]=a[31]+a[32]+...+a[40]
也就是101000从右向左数第一个1,把1及1后边的0去掉(把1000去掉),让a[100001]一直加到a[101000]
上两个图,就看清楚了
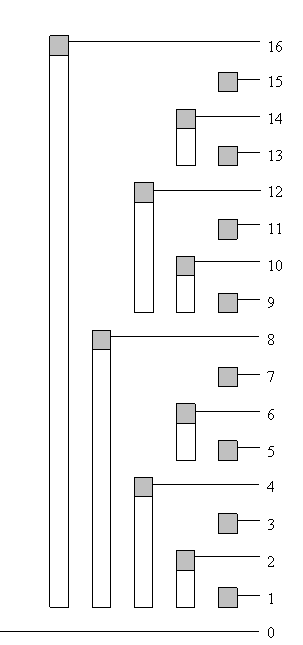
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| a |
1 |
0 |
2 |
1 |
1 |
3 |
0 |
4 |
2 |
5 |
2 |
2 |
3 |
1 |
0 |
2 |
灰色的是tree[i]大家可以把1~16转换为二进制验证一下
再上个图片
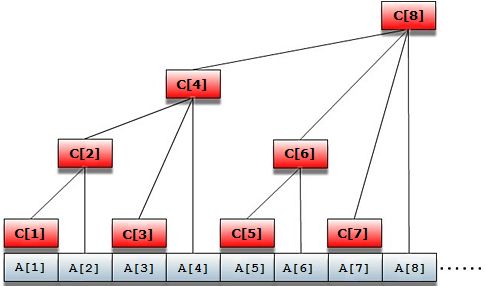
c是tree数组
明白了吗?
那则么求出从右向左数第一个1和它后边的0呢?
奥妙二:怎么求出从右向左数第一个1和它后边的0?
很简单。
知道补码肿么回事吗?正数的补码,不变;负数的补码取反加1,或者说,从右向左数一直不要变,直到第一个1,把1左边的数取反,这个大家都懂吧~
好的,继续。给你一个数x(一定是正数哦),求出他从右向左数第一个1和它后边的0?
1.求出它的补码,0-x
2.x与0-x相与
设出从右向左数第一个1和它后边的0这个数为low(x)
则low(x)=x&(-x)
奥妙三:求和
有了上边的基础,求和就好理解了
例如,求sum(13) 前13个数的和
13变身-------->1101 再变身 (先什么都不去掉)
--------->1101(去掉1,lowbit(1101))
---------->1100(去掉100,lowbit(100))
---------->1000
所以 sum[1101]=tree[1101]+tree[1100]+tree[1000]
也就是sum[13]=tree[13]+tree[12]+tree[8]
为什么这么算是对的?
好,复习一下奥妙二
tree[13]=a[13]
tree[12]=a[9]+a[10]+a[11]+a[12]
tree[8]=a[8]+a[7]+...+a[1]
很神奇吧~~~~~~
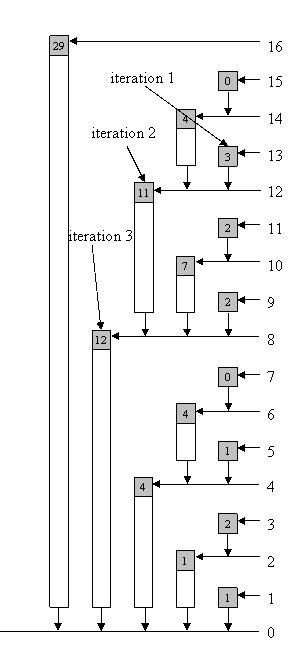
上个图:
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| a |
1 |
0 |
2 |
1 |
1 |
3 |
0 |
4 |
2 |
5 |
2 |
2 |
3 |
1 |
0 |
2 |
求sum[13]
写个求和函数
#define lowbit(x) ((x)&(-x))
int getsum(int i)
{
int sum=0;
while(i>0)
{
sum+=tree[i];
i-=lowbit(i);
}
return sum;
}
奥妙四:更新
更新一个数a[i],就得连带着更新存着a[i]的一些tree数组。怎么更新?想想~~~
没错!每次给i加lowbit(i)即可
举个栗子:)
更新a[5],比如给a[5]加上个新值nval
0101(+lowbit(0101))------->0110(+lowbit(0110))------->1000(+lowbit(1000))-------->10000
tree[5]+=nval tree[6]+=nval tree[8]+=nval tree[16]+=nval
上个图
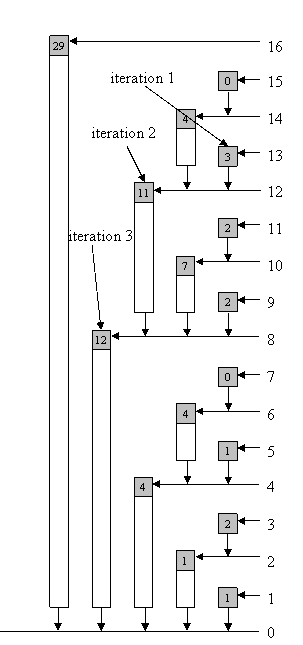
| |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
| a |
1 |
0 |
2 |
1 |
1 |
3 |
0 |
4 |
2 |
5 |
2 |
2 |
3 |
1 |
0 |
2 |
给a[5]加-1
写个函数:
#define lowbit(x) ((x)&(-x))
void update(int i,int val)
{
while(i<=n)
{
tree[i]+=val;
i+=lowbit(i);
}
}
对树状数组的进一步理解
很多人觉得树状数组很抽象,其实我的感觉也是一样。只是有些事如果想明白了,树状数组也是不难理解的。
下面我将进一步阐述我对树状数组的理解,既供大家参考,同时也是自己对树状数组的巩固。仅以一维为例,多维的推广即可。
一维:int c[N];
首先有一件事是大家必须清楚的:我们所有的操作(Lowbit(), Modify(), Getsum())都是对实实在在的 c[] 数组做的,因为我们只定义了 c[] 数组。但实际上我们却是在对一个假想的 a[] 数组进行操作。虽然这个 a[] 数组是假想出来的,但对我们来说却来得比 c[] 数组更加真实。c[] 数组只不过是为 a[] 数组服务的(注:因为对 a[] 数组来说,修改某个元素的值是 O(1) 的,但查询某个区间的和却是 O(n) 的,这在查询量很大的时候是根本不能满足要求的。现在有了 c[] 数组,可以使上述两个操作的时间均为 O(logn),从而大大降低了整体的复杂度,所以说 c[] 数组是为 a[] 数组服务的)。这一点想明白了,接下来的就都好理解了。
模式一:对数组 a[] 的某个元素作修改(O(logn)),查询某个区间内所有元素的和(O(logn))
这是树状数组比较常用的模式。比较难理解的地方在于 Modify() 和 Getsum() 两个函数中的 “i += Lowbit(i)” 和 “i -= Lowbit(i)” 的意义。先贴一张大家司空见惯的图吧:
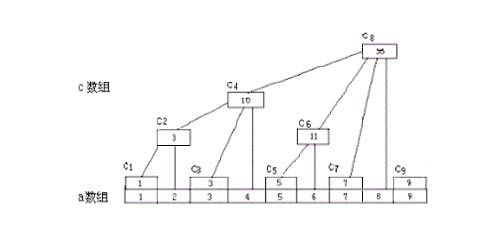
从这个图中大家可以清楚地看到,c[] 数组呈“树”状分布在 a[] 上,它的每一个元素都“管”着 a[] 中的一个或多个元素,而这样的关系正是利用了二进制的思想。
Modify(i, num): 现在我要对数组 a[] 中的第 i 个元素加上 num。那么为了维护 c[] 数组,我就必须要把 c[] 中所有“管”着 a[i] 的 c[i] 全部加上 num,这样才能随时保证 Getsum(i) 操作的正确性。而 "i += Lowbit(i)" 正是依次访问所有包含 a[i] 的 c[i] 的过程。
Getsum(i): 求和正好反过来,每次 “i -= Lowbit(i)” 依次求 a[i] 之前的某一段和。因为 c[i] 有这样一个性质:Lowbit(i) 的值即为 c[i] “管”着 a[i] 中元素的个数,比如 i = (101100)B,那么 c[i] 就是从 a[i] 开始往前数(100)B = 4 个元素的和,也就是 c[i] = a[i] + a[i - 1] + a[i - 2] + a[i - 3]。那么每次减去 Lowbit(i) 就是依次跳过当前 c[i] 所能管辖的范围,以便不重不漏地求出所有 a[i] 之前的元素之和。
模式二:随时修改数组 a[] 中某个区间的值(O(1)),查询某个元素的值(O(logn))
在这种模式下,a[i] 已经不再表示真实的值了,只不过是一个没有意义的、用来辅助的数组。这时我们真正需要的是另一个假想的数组 b[],b[i] 才表示真实的元素值。但 c[] 数组却始终是为 a[] 数组服务的,这一点大家要明确。此时 Getsum(i) 虽然也是求 a[i] 之前的元素和,但它现在表示的是实际我要的值,也就是 b[i]。
比如现在我要对图1 中 a[] 数组中红色区域的值全部加1。当然你可以用模式一的 Modify(i) 对该区间内的每一个元素都修改一次,但如果这个区间很大,那么每次修改的复杂度就都是 O(nlogn),m 次修改就是 O(mnlogn),这在 m 和 n 很大的时候仍是不满足要求的。这时模式二便派上了用场。我只要将该区域的第一个元素 +1,最后一个元素的下一位置 -1,对每个位置 Getsum(i) 以后的值见图2:
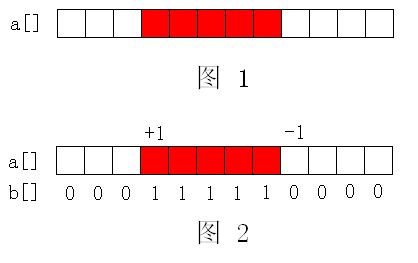
相信大家已经看得很清楚了,数组 b[] 正是我们想要的结果。模式二难理解主要在于 a[] 数组的意义。这时请不要再管 a[i] 表示什么,a[i] 已经没有意义了,我们需要的是 b[i]!但模式二同样存在一个缺陷,如果要对某个区间内的元素求和,就必须对该区间内的每个位置都作一次 Getsum(i),求出所有位置的真实元素值然后累加,这样复杂度又变成 O(nlogn) 了。所以要分清两种模式的优缺点,根据题目的条件选择合适的模式,灵活应变!
顺便给出二维树状数组模式二的修改方法:
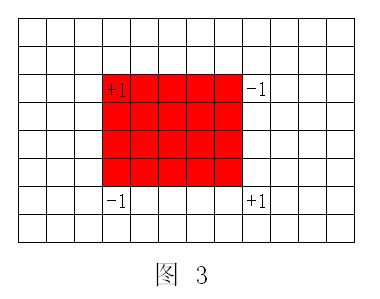
 从这个图中大家可以清楚地看到,c[] 数组呈“树”状分布在 a[] 上,它的每一个元素都“管”着 a[] 中的一个或多个元素,而这样的关系正是利用了二进制的思想。
从这个图中大家可以清楚地看到,c[] 数组呈“树”状分布在 a[] 上,它的每一个元素都“管”着 a[] 中的一个或多个元素,而这样的关系正是利用了二进制的思想。