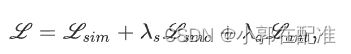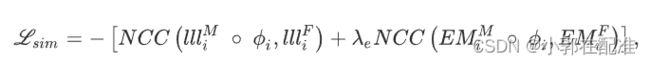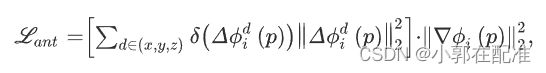医疗图像配准论文学习——AMnet（2023）自适应多级配准网络（

论文原文链接

前言

本文提出一种自适应多级配准网络（AMNet），以保持变形场的连续性，实现三维脑MR图像的高性能配准。首先，设计一种具有自适应增长策略的轻量级配准网络，从多级小波子带中学习变形场，便于全局和局部优化，实现高性能配准;其次，我们的AMNet设计用于图像配准，根据一个区域的变形复杂程度调整其局部重要性，从而提高配准效率并保持变形场的连续性。

key word：

Deformable registration、Adaptation、Multi-level、Wavelet transformation

一、介绍

传统的配准方法（基于特征、基于区域、基于几何量等）已经在图像配准上取得了成功，但这样的方法往往效率低、时间慢、无法共享参数（也就是说对每一对图像都需要搜索可变形变形场deformable transformation field）。这些年深度学习的方法进入配准领域，尽管训练基于深度学习的配准模型通常计算成本很高，但一旦训练了网络，配准就可以在几秒钟内完成，并在一次正向传递中估计全尺寸变形场。根据推导变形场的机理，这些深度配准方法可分为单级配准和多级配准。前者仅从一个分辨率级别或尺度导出变形场，而后者通常基于从粗到细的方案学习变形。根据搜索空间，单级配准模型可以进一步分为图像配准image-wise registration和补丁配准patch-wise registration。

图像单级配准模型通常构建在具有编码器-解码器架构的U-Net模型之上。尽管特征是从不同的图层和比例生成的，但最终仅使用全连接的图层或最高分辨率的比例来导出变形场。因此，直接在原始输入图像上搜索最佳变换的图像配准方案（在最高或最精细的分辨率级别），没有对变换进行初始估计的情况下，这种优化处理大位移时通常很慢，更容易陷入局部优化.此外，图像方法更侧重于全局上下文信息，限制了网络捕获复杂局部变形的能力。

补丁单级配准模型提高了计算效率和捕获局部变形的能力。 在这样的配准框架中，首先将输入图像分成小块，然后，在这些单独的块内限制变形场的搜索，以便快速进行变形学习。然后将来自补丁的变形场组合成一个全局变形场，以扭曲整个运动图像。尽管基于补丁的方法减轻了内存需求的负担，并且可以捕获更详细和微妙的局部变形，但这些模型可能面临一些重大限制。首先，如图1（a）所示，块之间的大变形可能导致近距离块的解剖特征出现严重的不一致性。因此，很难保持不同块之间的连续性，从而导致变形场的不连续性。此外，过度关注局部变形可能会导致陷入局部优化。

​ 具有大变形的 输入图像对的示例。补丁选择策略遵循 Fan等人（2019）的策略。三个不同颜色的框表示三个选定的相邻图块，大小为 64 × 64 × 64，相邻色块重叠 24 个体素。（b） 缩小采样图像的示例。左：基于高斯的下采样。右：基于小波的下采样（仅显示低频图像）。

 为了解决单级配准的局限性，多级配准以从粗到细的方式同时捕获全局和局部变形。根据不同的网络结构，多级注配准大致可分为多分支配准和多解析配准。

所谓多分支配准模型，是通过以下三种方式处理针对某些特定任务的子网络的大规模变形场。首先，已经有了仿射和可变形图像配准框架，通过它们来学习全局仿射变换参数和精细变形场。 其次，已经提出了一些不同精度的方法，通过堆叠多个网络来逐步估计部分变形。第三，通过组合全局和局部网络来执行多分支配准，以进行图像和补丁变形估计。这些方法通过多步渐进变形估计，提高了大规模变形的配准性能。当然，在基于补丁的全局-局部配准框架中，保持变形场的连续性是具有挑战性的，主要原因是由于局部子网络中补丁的分裂和组合。此外，这些具有多个子网的模型的复杂性给GPU的内存带来了巨大的负担，从而限制了收敛速度和配准稳定性。此外，这些网络的性能可能会受到级联传播引起的累积误差的影响。

多分辨率配准模型从最低分辨率级别开始，以不同的分辨率执行。 可以使用不同的下采样方案构建多分辨率图像金字塔，例如池化操作（Lee 等人，2020 年）、高斯滤波（Hering 等人，2019 年）和插值操作（Mok 和 Chung，2020 年）。这些方法首先计算低分辨率图像的全局变换，作为配准的初始变换估计，并重点关注高分辨率水平的局部变形。这些方法具有更有效的变形搜索和估计的优点;然而，用于构建多分辨率金字塔的下采样方案不可避免地会导致特征信息的丢失，导致图像中的纹理texture或空间混叠 spatial aliasing较弱（如图1（b）左侧）。如何更好地利用图像信息，降低网络复杂度，还有待探索。

综上所述，目前的单级配准方法，特别是基于补丁的方法，在处理大变形时难以保持变形场的连续性。对于目前的多层次配准，还有两大挑战有待探索。一方面，复杂的多分支模型可能高度依赖计算资源，收敛速度慢;另一方面，目前用于构建多分辨率图像金字塔的方案可能本质上无法充分利用图像信息，从而导致次优配准结果。

在本文中，我们旨在更全面地利用图像信息来提高配准性能，同时在应对复杂的变形和变化时保持变形场的连续性。我们提出了一种新颖的自适应多级网络（AMNet），以在一次正向传递中有效地捕获全局和复杂的局部变形。所提出的AMNet采用小波变换构建，以便更完整地利用低频全局信息和高频局部信息。对于高分辨率水平配准，AMNet根据其变形复杂性逐步调整具有更新重要性的区域，从而实现对大型或复杂变形的自适应聚焦并保持变形场的连续性。

​ AMNet框架由三个主要模块组成。（a）多级小波金字塔构造：从输入的运动图像和固定图像出发，基于三维离散小波变换（3D-DWT）构建具有四个分辨率级别的图像金字塔。（b） 适应性增长配准网络：来自AMNet的配准网络随着图像分辨率的提高而自适应地深化，以调整对全球-局部位移的关注。网络中的红色虚线表示新的网络图层在当前级别进行扩展。绿色虚线表示网络的当前级别共享上一级别的模型参数。（c）信息重要性适应：AMNet的适应能力主要体现在分辨率自适应、频率自适应和将配准重点从全局背景调整到局部变形的重要性适应三个方面。

二、方法

1.相关工作

小波变换：如Luo等人（2020）所述，小波变换可以实现与池化或插值操作相同的空间分辨率降低效果，而不会丢失任何信息。小波已被证明在传统的多分辨率配准方法中是有效的，可以避免局部最小值并减轻拓扑变化或折叠。最近，传统的小波理论已经与深度学习的优势相结合，并应用于图像分析任务，例如超分辨率（Liu等人，2018），图像合成（Qu等人，2020）和视差估计（Luo等人，2020).然而，小波理论尚未用于基于深度学习的配准。这主要是因为将图像分解为多频小波子带可能会大大增加配准过程的复杂性。例如，小波变换将3D图像分解为8个子带图像，如何利用这些低频和高频子带图像进行配准还有待研究。

由于本人没有学过信号处理，不太清楚小波变换，先学习这篇文章：图像的小波处理，主要讲的是2D方法，离散小波变换将一幅图象分解为大小，位置和方向都不同的分量。一个图像作小波分解后，可得一系列不同分辨率的子图像，小波变换正是沿着多分辨率这条线发展起来的。之后去读了一下这篇论文：基于3D离散小波变换的特征提取。与二维方法相比，将数据隔离到频率子带中的3D-DWT可以被视为更先进的3D编码预处理方法。它考虑了 3D 数据立方体的相关性，有助于改善压缩。基本思想是将信号呈现为小波的叠加。3D-DWT的优势在于在水平，垂直和深度方向上分解体积数据，而2D-DWT仅在水平和垂直维度上分解。3D-DWT 由张量积构造：

 图像的空间（水平和垂直）域和光谱维度分别由x、y和z方向表示，在应用单级分解之后将3D数据分解为八个子带。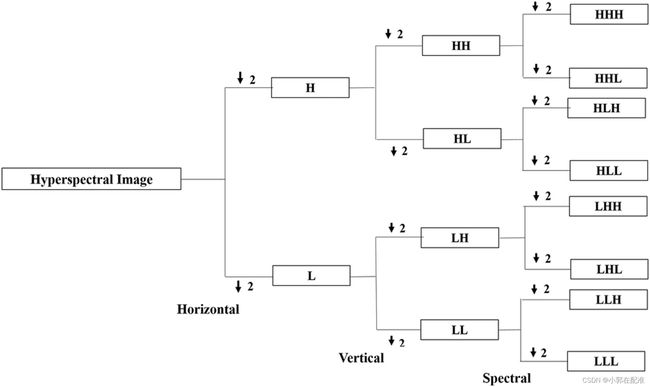

在水平垂直和频谱方向上通过低通滤波器的子带称为LLL。该波段是指数据立方体的近似值。数据立方体的顶点角度由HHH波段表示，该波段在水平，垂直和光谱方向上通过高通滤波器。

2.主要方法

这篇论文提取图像特征的方法就是基于这样的小波变换。

2.1多级小波金字塔构造

这种3D离散小波被用于构建多级图像金字塔，并发送到不同层的AMnet，这使得AMNet能够充分利用来自多频和多级小波子带图像的有用的补充信息（见上图（a））。每个金字塔包含四个分辨率级别：级别 0 对应于最高分辨率或最精细级别（也是原始输入图像），级别 3 表示最低分辨率或最粗糙级别。对于每个级别，有八个子波段图像，分别是hhh，hhl，hlh，hll，lhh，lhl，llh，lll。lll表示3d图像的低频分量或平均全局信息，而其他七个象限表示3D图像中的高频分量或局部细节。'l' 和 'h' 分别表示低通和高通滤波器。低频子波段用于学习全局变形，而其余的七个高频子波段融合成能量图（EM）来学习局部细节的变形。这允许模型同时考虑全局和局部优化，并降低计算复杂性。

点（x,y,z）处的EM可以被表示为：​

由7个高频子波段图像生成的EM图像反映了原始图像的显著特征，特别是边缘特征。这促使配准网络格外关注显著性感知信息，以实现结构对齐。配准过程从最粗糙的级别开始。粗略水平的估计值用于初始化金字塔下一级更精细水平的变形。这个过程传播到金字塔的最精细层次。

​ （a）第一级3D-DWT子带图像。（b） 在高分辨率水平上通过不同的协调参数计算局部重要性。

 注：论文中lll部分和sourse肉眼难以区分，我去学习2d小波变换图像处理的时候也发现，低频部分和原图基本一致，看不出来什么区别。也就是说其实我们肉眼可以识别的部分其实大多都是低频部分喽。高频的只有一些纹理、边缘之类的。个人的粗鄙之见，不一定正确哈，有大佬指正万分感谢。

2.2自适应增长配准网络

AMNet被设计为一个轻量级网络，具有自适应生长策略，以多级方式估计变形场。如图2所示，来自AMNetl3的配准网络到最后的AMNetl0随着图像分辨率的提高而自适应地深化，以调整对全局-局部位移的关注。这允许网络的浅层从低分辨率图像中学习全局变形，而深层可以从高分辨率图像中学习精细变形。

2.3信息重要性适配

我们网络的适应能力主要体现在三个方面：分辨率自适应、频率适应和局部重要性适应，用于将配准重点从全局上下文调整到局部变形。

首先，为了实现快速准确的图像配准，我们遵循多分辨率配准的思路，并在随后的高分辨率水平上进行计算，得到延长和细化的粗网格解决方案。因此，我们的网络使用渐进式学习策略学习变形场，允许从信息较少的低分辨率图像到信息更详细的高分辨率图像的更好适应性，特别是对于大变形。

其次，由于低频子波段反映了三维图像的全局平均信息，因此可以从低频子波段获得全局变形场;而具有局部细节的高频子带则用于获得组织边界处的局部变形。因此，我们的AMNet首先从3级的低频子带学习全局变形场，然后采取EM（由七个高频子带图像生成的energy map）和低频子带图像作为level 2、level 1的两个输入.这使我们的模型能够更好地从具有全局信息的低频特征适应具有边界感知重要性的高频特征。

第三，由于全局对齐是在低分辨率级别（级别 3 和 2）执行的，因此并非所有区域对于高分辨率图像级别（级别 1 和 0）的配准都具有相同的重要性。而随后在高分辨率水平上对图像对的精细对齐又很容易受到具有大或复杂局部变形的区域的影响。因此，我们提出了一种局部重要性适应机制，以定位困难/复杂的区域，同时捕获全球上下文信息。我们的AMNet将整个图像作为每个级别的输入。我们利用差异图（DM，difference map） 和固定图像来guide大型/复杂变形结构的局部优化。DM是计算为扭曲运动图像和固定图像之间的强度差，然后作用于该图像对。如图3（b）所示，差异图中的亮点是难以配准的区域，这些区域包含复杂的变形，需要重点关注以进一步细化。随后，DM归一化为 [0，1] 以反映图像中需要进一步配准的区域的重要性级别。

注：这段文字描述了这篇文章的核心立意，有需要的同学可以看看原文：

3.网络

 

 整体是一个类似unet的结构，需要注意的是，不同级的输入不一样，前三个阶段用小波子带图像训练，最后一个阶段用原始图像训练。每个阶段的训练都是基于卷积来的（这里有一个思考，如果使用transformer会不会是一个创新点？）

网络细节公式太多了，大家直接看原文：

4.损失函数

因为每一个level都会进行训练，输出一个变形场，所以每一个level都会有一个损失函数，这里损失函数由三部分组成：

 第一项是我们的相似性度量，局部归一化互相关NCC，

 分为两个部分，低频小波子带部分和能量图部分，这里的参数lamda在级别 0 和 3 处设置为 0;否则，它设置为 1。我们在能量图上也计算图像相似性，是为了确保组织边界可以比仅在低频图像中比较图像相似性时更准确地配准。

第二项是变形场的平滑度

 每一个体素在变形场中的梯度。我们知道图像对齐和变形场平滑度之间的平衡很难控制，因为图像对中的所有像素都有不同程度的变形。当由于过度正则化而为平滑度约束分配较大的权重时，配准结果将不准确。反之，较小的权重将提高配准精度，但会导致变形场中的折叠。在以前的研究中，使用反折叠约束来动态控制平滑度权重（Zhang，2018，Huang等，2021）。在这里，我们还在目标函数中使用了这样的反折叠约束，如下所示：（这个约束我没太看明白，之前看的论文里约束反转都是通过限制变形场雅可比矩阵中负数的个数，这个估计是比较新的一个约束）

 5.实验部分略

tips:未来工作：将这个网络引入多模态配准