【数据结构与算法】——第二章：线性表

 ============================ 【说明】 ===================================================
  大家好，本专栏是 数据结构与算法， 该科目是计算机类专业必修课之一，比较重要也比较基础，有想从事算法研究的同学，这些内容是专/本科、甚至硕士期间较为基础的内容，适用范围较广：大学专业课学习、考研复习等。
  通过自己的理解进行整理，希望大家积极交流、探讨，多给意见。后面也会给大家更新其他一些知识。若有侵权，联系删除！共同维护网络知识权利！

1、线性表

1.1 基本概念

  线性表：具有相同数据类型的的零个或多个数据元素的有限序列。
  例子：小朋友放学排队。
  关键：首先，它是一个序列。也就是说，元素之间是有顺序的，若元素存在多个，则第一个元素无前驱，最后一个元素无后继，其他每个元素都有且只有一个前驱和后继。如果一个小朋友去拉两个小朋友后面的衣服，那就不可以排成一队了；同样，如果一个小朋友后面的衣服，被两个甚至多个小朋友拉扯，这其实是在打架，而不是有序排队。
  然后，线性表强调是有限的。小朋友班级人数是有限的，元素个数当然也是有限的。事实上，在计算机中处理的对象都是有限的，那种无限的数列，只存在于数学的概念中。

  所以线性表元素的个数n (n≥0)定义为线性表的长度，当n=0时，称为空表。

1.2 线性表基本操作

  为了让小朋友有秩序地出入，所以就考虑给他们排一个队，并且是长期使用的顺序，这个考虑和安排的过程其实就是一个线性表的创建和初始化过程。
  把小朋友排好队后，发现有的高有的矮，队伍很难看，于是就让小朋友解散重新排．这是一个线性表重置为空表的操作。
  排好了队，我们随时可以叫出队伍某一位置的小朋友名字及他的具体情况。比如有家长问，队伍里第五个孩子，怎么这么调皮，他叫什么名字呀，老师可以很快告诉这位家长。这种可以根据位序得到数据元素也是一种很重要的线性表操作。
  有时我们想知道，某个小朋友，比如xx是否是班里的小朋友，老师会告诉我说，不是，麦兜在春田花花幼儿园里，不在我们幼儿园。这种查找某个元素是否存在的操作很常用。
  班里现在到底有多少个小朋友呀，这种获得线性表长度的问题也很普遍。
  对于一个幼儿园来说，加入一个新的小朋友到队列中，或因某个小朋友生病，需要移除某个位置，都是很正常的情况。对于一个线性表来说，插入数据和删除数据都是必须的操作。
  线性表除了以上基本操作，还有更为复杂的操作，例如实现两个线性表集合的并集操作等。

2、线性表的顺序存储

  顺序存储：指的是用一段地址连续的存储单元依次存储线性表的数据元素。

  顺序存储三个属性：
  存储空间的起始位置：数组data，它的存储位置就是存储空间的存储位置。
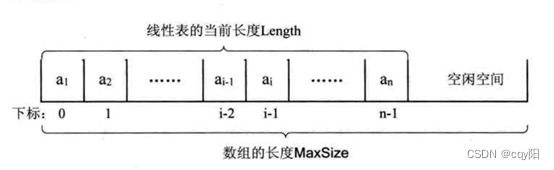
  线性表的最大存储容量：数组长度MaxSize
  线性表的当前长度：length

  数组长度和线性表长度区别：
  数组的长度是存放线性表的存储空间的长度，存储分配后这个量是一般是不变的。
  线性表的长度是线性表中数据元素的个数，随着线性表插入和删除操作的进行，这个量是变化的。
  在任意时刻，线性表的长度应该小于等于数组的长度。

  内存中的地址，就和图书馆或电影院里的座位一样，都是有编号的。存储器中的每个存储单元都有自己的编号，这个编号称为地址。
  由于每个数据元素，不管它是整型、实型还是字符型，它都是需要占用一定的存储单元空间的。
  假设占用的是c个存储单元，那么线性表中第i+1个数据元素的存储位置和第i个数据元素的存储位置满足下列关系：

  对于第i个数据元素ai的存储位置可以由al推算得出：

2.1 线性表顺序存储的插入与删除

  (1) 插入操作


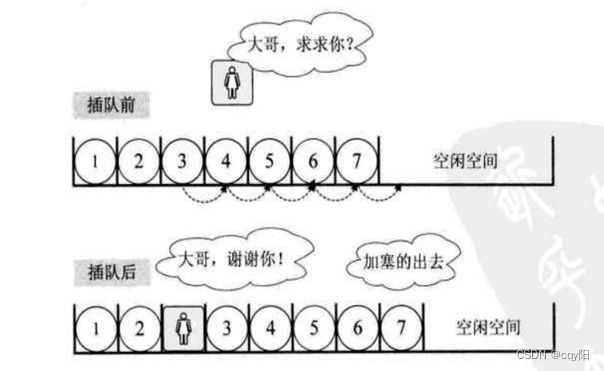
  思路（代码略）
  如果插入位置不合理，抛出异常；
  如果线性表长度大于等于数组长度，则抛出异常或动态增加容量；
  从最后一个元素开始向前遍历到第i个位置，分别将它们都向后移动一个位置；
  将要插入元素填入位置i处；
  表长加1。

  
  (2) 删除操作


  思路
  如果删除位置不合理，抛出异常；
  取出删除元素；
  从删除元素位置开始遍历到最后一个元素位置，分别将它们都向前移动一个位置；
  表长减1。

  
  

  (3) 优缺点

3、线性表的链式存储

为什么会有链式存储结构？

  为什么当插入和删除时，就要移动大量元素，仔细分析后，发现原因就在于相邻两元素的存储位置也具有邻居关系。它们编号是1，2，3， ，n，它们在内存中的位置也是挨着的，中间没有空隙，当然就无法快速介入，而删除后，当中就会留出空隙，自然需要弥补。问题就出在这里。
  线性表的链式存储结构的特点是用一组任意的存储单元存储线性表的数据元素，这组存储单元可以是连续的，也可以是不连续的。这就意味着，这些数据元素可以存在内存未被占用的任意位置。

  以前在顺序结构中，每个数据元素只需要存数据元素信息就可以了。现在链式结构中，除了要存数据元素信息外，还要存储它的后继元素的存储地址。
  因此，为了表示每个数据元素ai与其直接后继数据元素之间的逻辑关系，对数据元素a1来说，除了存储其本身的信息之外，还需存储一个指示其直接后继的信息（即直接后继的存储位置）。我们把存储数据元素信息的域称为数据域，把存储直接后继位置的域称为指针域。

  对于线性表来说，总得有个头有个尾，链表也不例外。我们把链表中第一个结点的存储位置叫做头指针，那么整个链表的存取就必须是从头指针开始进行了。之后的每一个结点，其实就是上一个的后继指针指向的位置。想象一下，最后一个结点，它的指针指向哪里？
  最后一个，当然就意味着直接后继不存在了，所以我们规定，线性链表的最后一个结点指针为“空"（通常用NULL或“ ^ ”符号表示）

  有时，我们为了更加方便地对链表进行操作，会在单链表的第一个结点前附设一个结点，称为头结点。头结点的数据域可以不存储任何信息，谁叫它是第一个呢，有这个特权。也可以存储如线性表的长度等附加信息，头结点的指针域存储指向第一个结点的指针。

  注意头结点和头指针的异同：

3.1 单链表

  (1) 单链表插入操作

  先来看单链表的插入。假设存储元素e的结点为s，要实现结点p、p->next和s 之间逻辑关系的变化、只需将结点s插入到结点p和p->next之间即可。可如何插入呢？

  根本用不着惊动其他结点，只需要让s->next和p->next的指针做一点改变即可。


  如果先p->next=s;再s->next=p->next;会怎么样？哈哈，因为此时第一句会使得将p->next给覆盖成s的地址了。那么s->next=p->next，其实就等于s->next=s，这样真正的拥有数据元素的结点就没了上级。这样的插入操作就是失败的，造成了临场掉链子的尴尬局面。所以这两句是无论如何不能反的，这点一定要注意。

  单链表第i个数据插入结点的算法思路

  
  (2) 单链表删除操作

  我们所要做的，实际上就是一步，p->next=p->next->next，用q来取代p->next。

  单链表第i个数据除结点的算法思路

3.2 静态链表

  其实C语言是个好东西，它具有的指针能力，使得它可以非常容易地操作内存中的地址和数据，这比其他高级语言更加灵活方便。后来的面向对象语言，如Java、C# 等，虽不使用指针，但因为启用了对象引用机制，从某种角度也间接实现了指针的某些作用。
  链表结构按照前面我们的讲法，它就没法实现了。怎么办呢？有人就想出来用数组来代替指针，来描述单链表。

  对数组第一个和最后一个元素作为特殊元素处理，不存数据。我们通常把未被使用的数组元素称为备用链表。而数组第一个元素，即下标为0的元素的cur 就存放备用链表的第一个结点的下标；而数组的最后一个元素的cur则存放第一个有数值的元素的下标，相当于单链表中的头结点作用。

  案例：

  (1) 静态链表插入操作

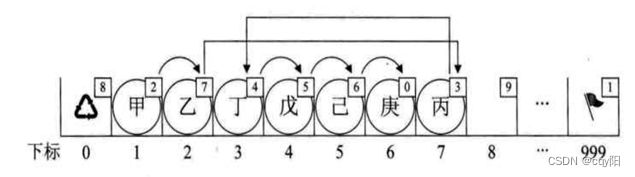
  (1) 静态链表删除操作

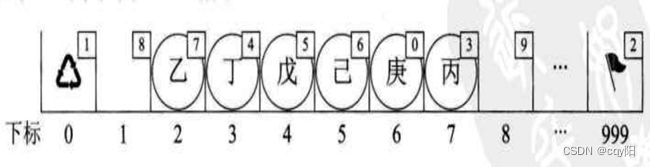
  (3) 静态链表优缺点

  静态链表是为没有指针的高级语言所设计。

3.3 循环链表

  将单链表中终端结点的指针端由空指针改为指向头结点，就使整个单链表形成一个环，这种头尾相接的单链表称为单循环链表，简称循环链表。

3.3 双向链表

  双向链表：在单链表的每个结点中，再设置一个指向其前驱结点的指针域。

4、线性表的顺序存储与链式存储的优缺点

  (1) 线性结构的特点
  1.只有一个首结点和一个尾结点
  2.除首尾结点外其他结点只有一个直接前驱和一个直接后继线性表第i个元素ai的存储位置：LOC(ai)=LOC(a1)+(i-1)×L
  3.顺序表的特点：逻辑上相邻的元素，物理上也相邻
  4.链式表的特点：逻辑上相邻的元素，物理上不一定相邻
  5.存取结构分为随机存取和顺序存取：随机存取就是直接存取，可以通过下标直接访问的数据结构，与存储位置无关，例如数组。
  6.非随机存取就是顺序存取，不能通过下标访问，只能按照存储顺序存取，与存储位置有关，例如链表。

  (2) 不同角度下优缺点对比

  若线性表需要频繁查找，很少进行插入和删除操作时，宜采用顺序存储结构。
  若需要频繁插入和删除时，宜采用单链表结构。
  比如说游戏开发中，对于用户注册的个人信息，除了注册时插入数据外，绝大多数情况都是读取，所以应该考虑用顺序存储结构。而游戏中的玩家的武器或者装备列表，随着玩家的游戏过程中，可能会随时增加或删除，此时再用顺序存储就不太合适了，单链表结构就可以大展拳脚。当然，这只是简单的类比，现实中的软件开发，要考虑的问题会复杂得多。

5、附习题

  (1) 线性表的顺序存储结构具有三个弱点:第一,在作插入或删除操作时,需要移动大量元素;第二,由于难以估计,必须预先分配较大的空间,往往使存储空间不能得到充分利用;第三,表的容量难以扩充。试问,线性表的链式存储结构是否一定能够克服上述三个弱点?请简述之。
  答：一般说链式存储结构克服了顺序存储结构的三个弱点。首先,插入、删除不需移动元素,只修改指针,时间复杂度为O(1);其次,不需要预先分配空间,可根据需要动态申请空间;其三,表容量只受可用内存空间的限制。其缺点是因为指针增加了空间开销,当空间不允许时,就不能克服顺序存储结构的缺点。

  (2) 在单链表和双向链表中,能否从当前结点出发访问到任何一个结点?

  答：在单链表中不能从当前结点(若当前结点不是第一结点)出发访问到任何一个结点。因为链表运算只能从头指针开始，访问到链表中每个结点。在双链表中从当前结点反向可以到第一结点，正向可以到最后结点，因而从当前结点出发可以访问到链表中任何一个结点。

  (3) 设双向循环链表中结点的数据域、前驱和后继指针域分别为data、pre和next,试写出在指针P所指结点之前插入一s结点的C语言描述语句。
  答：在指针P所指结点前插入结点s的语句如下：s->pre=p->pre; s->next=p; p->pre->next=s; p->pre=s;