用matlab求解线性规划
文章目录
-
- 1、用单纯形表求解线性规划
-
- 绘制单纯形表求解:
- 2、用matlab求解线性规划——linprog()函数
-
- 问题:
- 补充代码:显示出完整的影子价格向量
1、用单纯形表求解线性规划
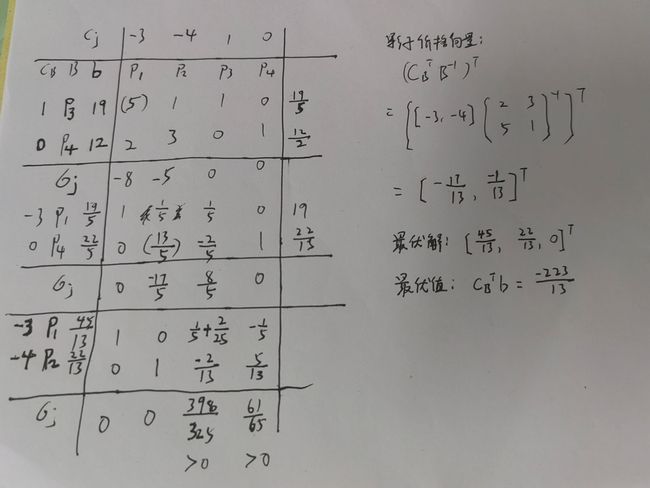
求解线性规划 m i n − 3 x 1 − 4 x 2 + x 3 min -3x_1-4x_2+x_3 min−3x1−4x2+x3,
约束条件为
2 x 1 + 3 x 2 ≤ 12 2x_1+3x_2≤12 2x1+3x2≤12
5 x 1 + x 2 + x 3 = 19 5x_1+x_2+x_3=19 5x1+x2+x3=19,
x 1 , x 2 , x 3 ≥ 0 x_1,x_2,x_3≥0 x1,x2,x3≥0.
绘制单纯形表求解:
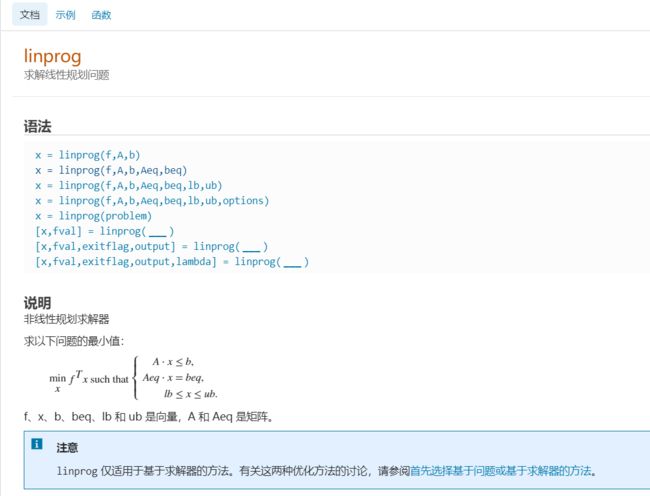
2、用matlab求解线性规划——linprog()函数
clc,clear,close all;
% 定义目标函数的系数向量
f = [-3; -4; 1];
% 定义不等式约束的系数矩阵和右侧常数向量
A = [2, 3, 0];
b = [12];
% 定义等式约束的系数矩阵和右侧常数向量
Aeq = [5, 1, 1];
beq = [19];
% 定义变量的边界
lb = zeros(3, 1); % 所有变量的下界都是0
% 使用linprog求解线性规划问题
[x, fval, exitflag, output, lambda] = linprog(f, A, b, Aeq, beq, lb);
% 输出结果
fprintf('最小值为: %.4f\n', fval);
fprintf('x1 = %.4f, x2 = %.4f, x3 = %.4f\n', x(1), x(2), x(3));
fprintf('\n')
disp('输出结果(以分数形式显示):')
fprintf('最小值为: %s\n', rats(fval));
fprintf('x1 =%s, x2 =%s, x3 =%s\n', rats(x(1)), rats(x(2)), rats(x(3)));
% 输出影子价格向量(以分数形式显示)
fprintf('影子价格向量为:\n');
disp(rats(lambda.ineqlin));
返回结果:
Optimal solution found.
最小值为: -17.1538
x1 = 3.4615, x2 = 1.6923, x3 = 0.0000
输出结果(以分数形式显示):
最小值为: -223/13
x1 = 45/13 , x2 = 22/13 , x3 = 0
影子价格向量为:
17/13
问题:
此处发现两个问题,主要体现在影子价格向量上:
1、影子价格少一个元素
2、影子价格向量元素和用代数公式法求解的结果差一个负号
通过查阅Mathworks官方文档,可以看到缺少负号并不是程序编写错误问题:
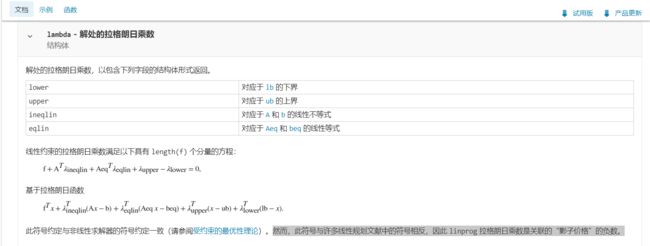
补充代码:显示出完整的影子价格向量
问题1的解决方法:需要将约束条件中的不等式全部写为等式。
因为将一个不等式和一个等式的约束条件传递给linprog函数时,它会计算一个相对较小的影子价格向量,其中包含了不等式约束的影响,而等式约束的影响通常不单独表示在影子价格向量中。
%% 约束条件全部为等式
disp('求解完整的影子价格向量:')
% 定义目标函数的系数向量
f = [-3; -4; 1];
% 定义不等式约束的系数矩阵和右侧常数向量
A = [2, 3, 0; 5, 1, 1];
b = [12; 19];
% 定义变量的边界
lb = zeros(3, 1); % 所有变量的下界都是0
% 使用linprog求解线性规划问题
[x, fval, exitflag, output, lambda] = linprog(f, A, b, [], [], lb);
% 输出结果
fprintf('最小值为: %.4f\n', fval);
fprintf('x1 = %.4f, x2 = %.4f, x3 = %.4f\n', x(1), x(2), x(3));
% 输出影子价格向量
fprintf('影子价格向量为:\n');
disp(lambda.ineqlin);
fprintf('\n')
disp('输出结果(以分数形式显示):')
fprintf('最小值为: %s\n', rats(fval));
fprintf('x1 =%s, x2 =%s, x3 =%s\n', rats(x(1)), rats(x(2)), rats(x(3)));
% 输出影子价格向量(以分数形式显示)
fprintf('影子价格向量为:\n');
disp(rats(lambda.ineqlin));
fprintf('\n')
返回结果:
求解完整的影子价格向量:
Optimal solution found.
最小值为: -17.1538
x1 = 3.4615, x2 = 1.6923, x3 = 0.0000
影子价格向量为:
1.3077
0.0769
输出结果(以分数形式显示):
最小值为: -223/13
x1 = 45/13 , x2 = 22/13 , x3 = 0
影子价格向量为:
17/13
1/13