2019.03.12 - 常见算法和数据结构
文章目录
- 抽象数据类型和面向对象编程
-
- 学习资料
- 示例:Bag类
- 数组
-
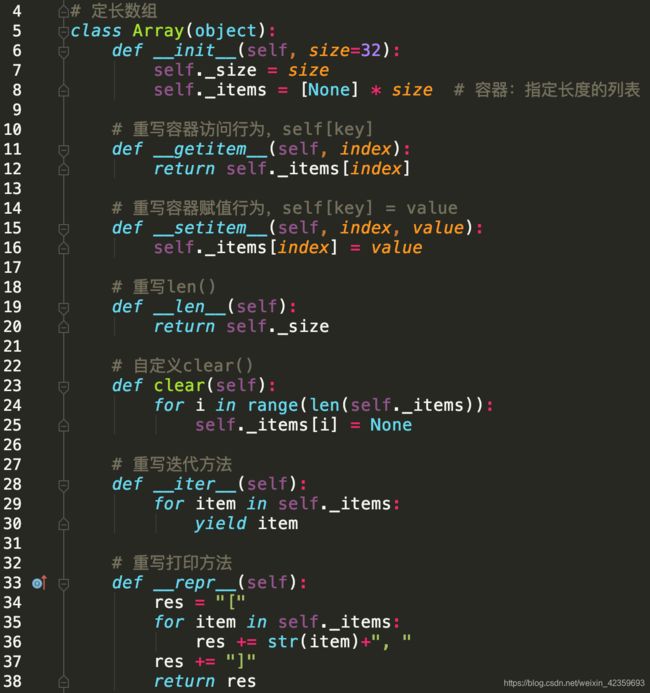
- 定长数组
- 链表
-
- 线性与链式结构
- 单链表
-
- 单链表结构
-
- LinkedList代码结构
-
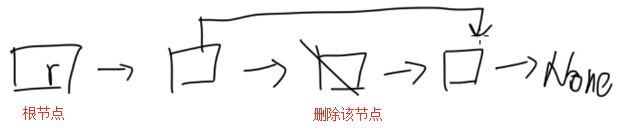
- delete操作示意图
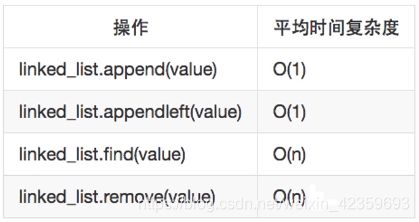
- 各操作的时间复杂度
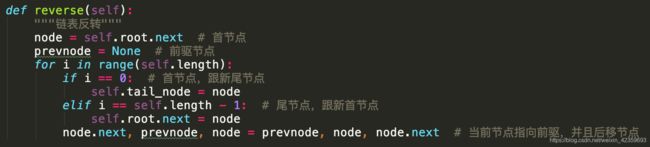
- 单链表反转
-
- 方案1:利用append_left
- 方案2:前驱与后继互换
- 双链表
-
- 双链表结构
-
- 循环双端链表
- CyclicDoubleLinkedList代码结构
- 时间复杂度
-
- 常见算法的时间复杂度
- 空间复杂度
-
- 常见数据结构的复杂度
- 常见结构与算法的时间复杂度
- 常见复杂度增长趋势
- 栈
-
- 栈结构
-
- Stack代码结构
-
- `collections.deque`
- 队列
-
- 队列结构
-
- Python实现
- golang实现
-
- 数组模拟队列
- 数组模拟环形队列
- 哈希表
-
- 哈希函数
-
- 哈希碰撞
-
- 解决方法
- 哈希函数的优化
- List vs Map vs Set
-
- 哈希表与二叉树
- 递归(Recursion)
-
- n的阶乘(n!)
-
- 递归思想剖析
- 递归模板
- 斐波那切数列(Fabonacci Array)
-
- F(6)的递归层级剖析
- 调用栈
-
- 调用栈的层级剖析
- 斐波那契数列的优化
-
- golang实现
- 分治(Divide & Conquer)
-
- 字符串变大写
- 分治模板
- 基础排序算法
-
- 冒泡排序
-
- golang实现
- 选择排序
-
- golang实现
- 插入排序
-
- golang实现
- 高级排序算法
-
- 分治法与归并排序
-
- 分治法
- 归并两个有序数组
- 快速排序
-
- golang实现
-
- 使用归并,不是指针
- 使用指针
- 树
-
- 基本概念
-
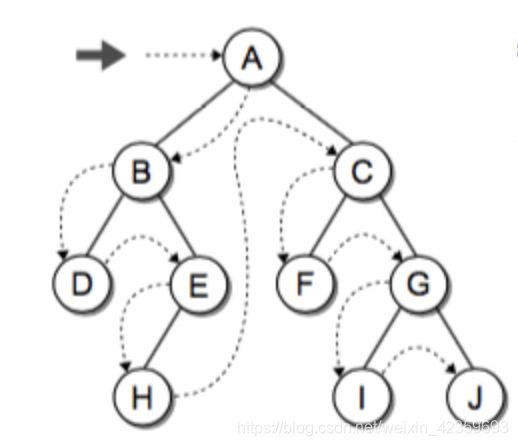
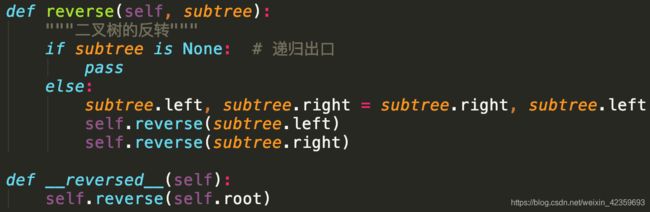
- 二叉树
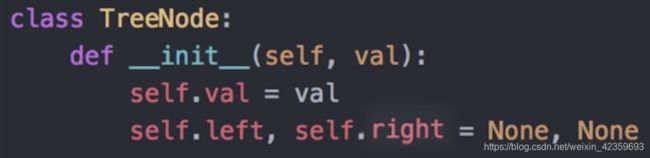
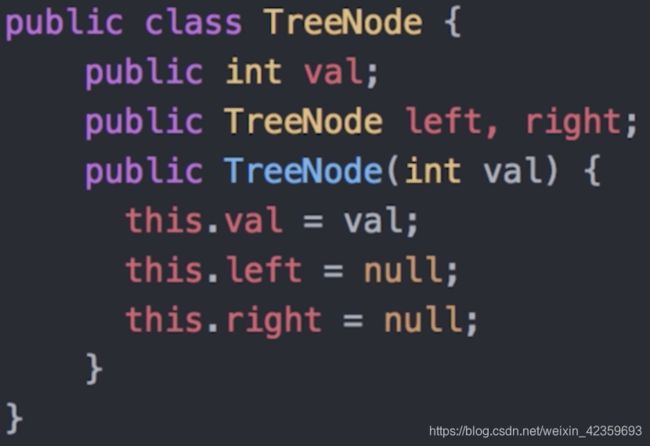
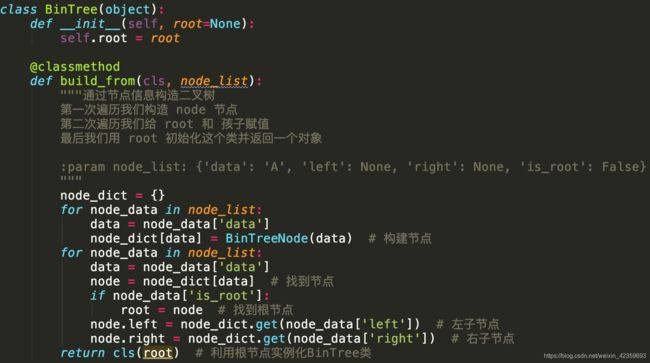
- 如何构建树节点
- 二叉搜索树
- 二叉树的遍历
-
- 遍历顺序
- 构建二叉树的代码实现
- 二叉查找树(Binary Search Tree, BST)的代码实现
-
- BST构建
- BST操作
-
- 查找
- 查找最小/大节点
- 插入
- 删除
- 堆(heap)
-
- 堆的概念介绍
- 堆的表示
- 堆的操作
-
- 插入新节点
- 删除根节点
- 堆排序
- 二分查找
-
- 线性查找
- 什么是二分查找(Binary Search)
- 代码模板
- 二分查找详细过程
- 相关模块
抽象数据类型和面向对象编程
学习资料
-
Python 中文数据结构和算法教程
-
Python 讲解笔记与代码 - Github
-
视频教程:极客时间-算法通关,参考理论讲解
-
视频教程:Python数据结构与算法教程
- 课程讲义:Python 算法与数据结构视频教程
-
利用class实现数据结构
- data
- method
-
Abstract Data Type, ADT:抽象数据类型
示例:Bag类
-
data:容器
-
method
- add:添加
- remove:删除
- len:查看长度
- iter:迭代
-
注意事项
- 选用DataStructure
- 能否操作 add 和 remove
- 效率如何
数组
定长数组
链表
线性与链式结构
- 线性结构:内存连续,下标访问
- 链式结构:内存不连续,不能下标访问,添加元素方便,通过遍历来寻找元素
单链表
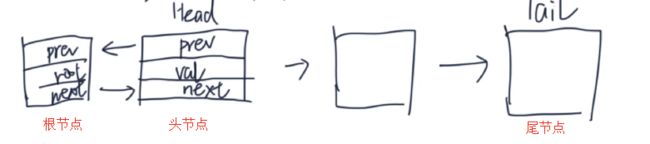
单链表结构
LinkedList代码结构
-
LinkedList
- data
- root, length, tail_node
- method
- init, is_empty,
__len__, append, appendleft, iter_node,__iter__, remove, find, popleft, clear, reverse
- init, is_empty,
- data
-
代码示例:
linked_list_adt.py
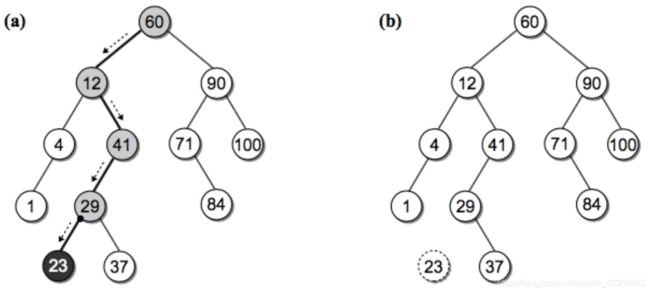
delete操作示意图
各操作的时间复杂度
单链表反转
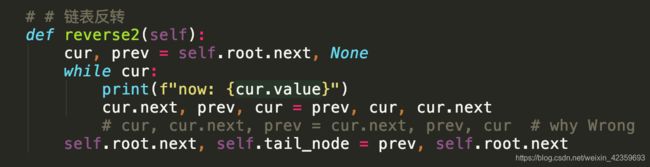
LinkedList.reverse()
方案1:利用append_left
方案2:前驱与后继互换
双链表
- 双链表又称双端链表
- 优化了单链表查询的低效率
双链表结构
循环双端链表
CyclicDoubleLinkedList代码结构
-
LinkedList
- data
- root, maxsize, length
- method
- headnode, tailnode, append, append_left, remove(O(1)), iter_node, iter_node_reverse
- data
-
代码实现:略
时间复杂度
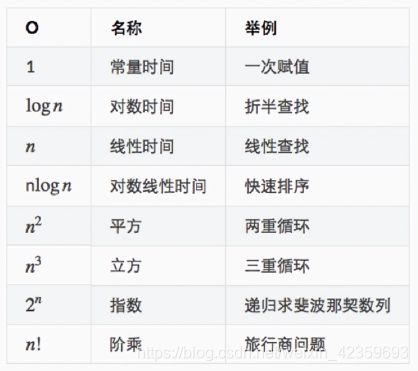
常见算法的时间复杂度
空间复杂度
常见数据结构的复杂度
常见结构与算法的时间复杂度
- 数据结构的复杂度:Big-O Algorithm Complexity Cheat Sheet
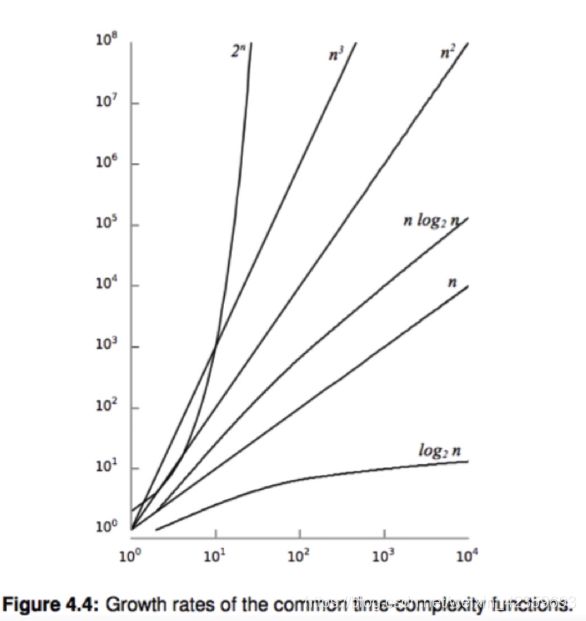
常见复杂度增长趋势
- 时间换空间,空间换时间
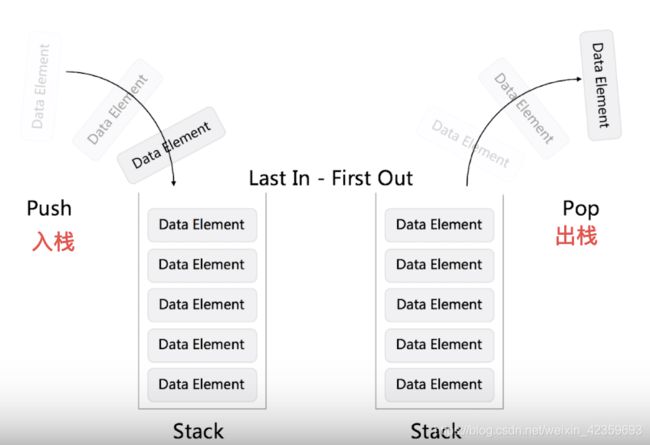
栈
- 栈
- 栈区
- 先进后出(last in first out)
栈结构
Stack代码结构
-
Stack
- data
- method
- push, pop, pop_left
-
代码实现:
stack_adt.py- 基于
list实现
- 基于
-
思考题:利用双端队列实现
- 基于
collections.deque实现
- 基于
collections.deque
python内置的 双端队列
- append, appendleft:追加元素,从队首加入元素
- extend, extendleft:拼接入元素
- maxlen:字段,最大长度
- pop, popleft
- remove
- clear:清空元素
- reverse:逆序
- rotate:把最右侧的元素放到最左侧(循环)
队列
队列结构
- 特点:先入先出(FIFO),有序,可能有maxSize。
- 实现方式:
- 数组/队列:进出元素可能需要挪动队列中的所有元素,效率差。【优化:环形数组】
- 链表。
Python实现
- 直接使用list即可实现。【最差方式】
class Queue:
"""队尾进,队首出"""
def __init__(self):
self._queue = []
def add(self, value):
self._queue.append(value)
def out(self):
return self._queue.pop(0)
golang实现
参考:尚硅谷-数组模拟队列
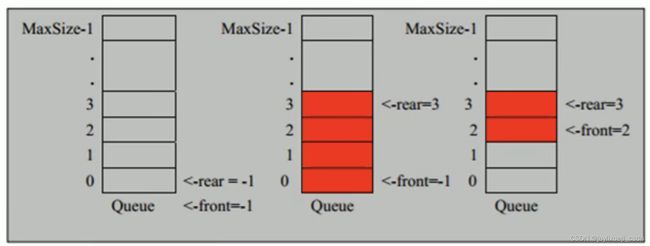
数组模拟队列
-
使用head和tail分别记录 队首(队首前一个) 和 队尾。
-
数据存入队列是add_queue:
- 将尾指针后移,tail+1。
- 若尾指针等于队列的最大下标MaxSize-1,则将数据存入 tail所指的数组元素中,否则无法存入。tail == MaxSize-1,则队列满了。
- 上面代码实现了基本队列结构,但是没有有效的利用数组/切片的空间。
- 优化:使用数组,实现一个环形的队列。
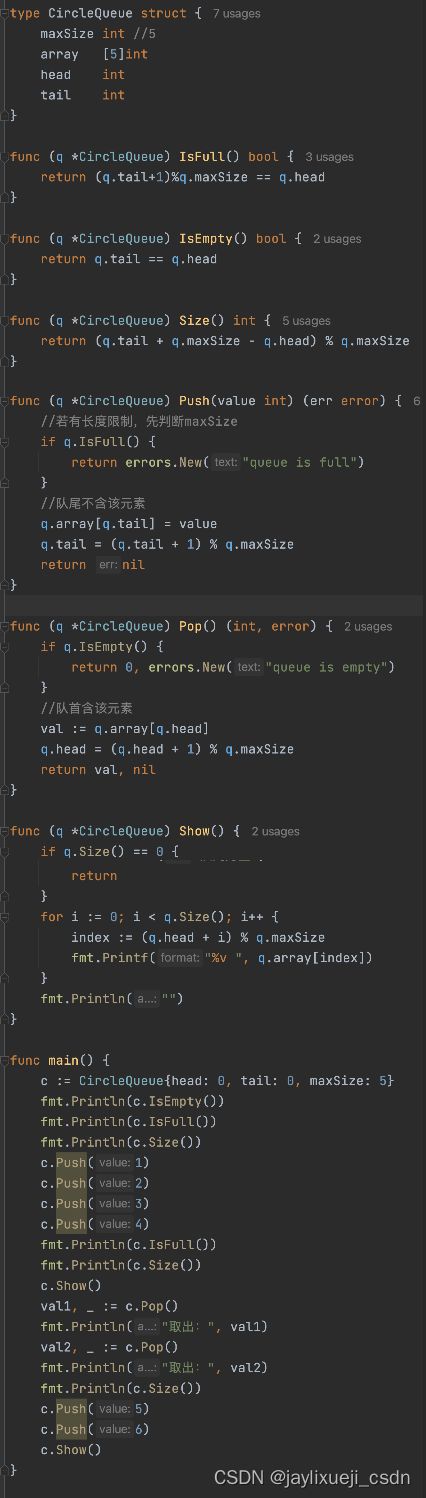
数组模拟环形队列
参考:尚硅谷-数组模拟循环队列
- head含该元素,tail也不含该元素。
- 如果前面是用数组实现的,为充分利用数组,可将数组看作是环形的。【取模%maxSize】
- 将队列容量空出一个作为约定,队列满的条件:
(tail+1)%maxSize == head。 tail==head为空。- 初始化,head=0,tail=0。
- 队列中元素的数量:
(tail + maxSize - head) % maxSize。
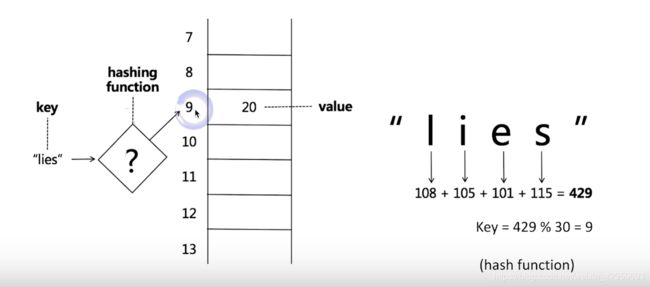
哈希表
哈希函数
哈希碰撞
解决方法
- 拉链法:每个槽位都存储为链表。碰撞过多时,查询的时间复杂度退化。
- 开放寻址法(open addressing):
- 线性探查法:当槽位被占用,寻找下一个可以使用的槽位。
- 二次探查法:当槽位被占用,以二次方作为偏移量。Python内置使用该方法。
- 双重散列法:二次哈希。
哈希函数的优化
- 装载因子:决定如何开辟新的内存空间
- 重哈希(Rehash)
List vs Map vs Set
- List即列表
- Map,即映射数据结构(KEY与Value),在Python中即为Dict字典
- Set,集合,不允许有重复的元素,也可理解为只有KEY的Map。
哈希表与二叉树
字典和集合一般是基于哈希表或二叉树实现。
| HashMap/HashSet | TreeMap/TreeSet | |
|---|---|---|
| 查询 | O(1) | O(logN) |
| 排序 | 无序 | 相对有序 |
- Python的Dict:基于HashMap
- Java有 HashMap与TreeMap
递归(Recursion)
递归的本质是循环,通过函数体进行的循环。
n的阶乘(n!)
递归思想剖析
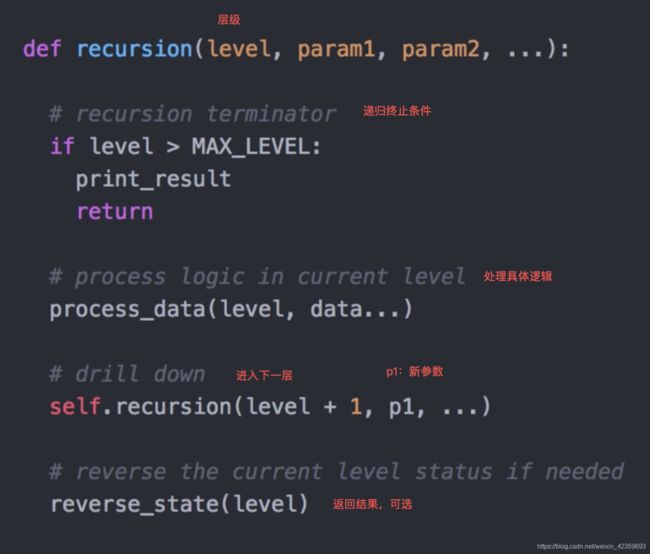
递归模板
- recursion terminator:递归终止条件
- level:递归层级
- process logic in current level:在当前层级,处理具体业务逻辑
- drill down:进入下层(p1:新参数)
- reverse:返回当前层级的结果,可选
斐波那切数列(Fabonacci Array)
- 斐波那切数列的示例:1, 1, 2, 3, 5, 8, 13, 21, 34, …
- 公式:
F(n-1) + F(n-2) - 代码示例:

- 注意:递归的傻瓜实现(千万不能作为面试题答案)
- 时间复杂度为:O(2**n),数字过大时会超过最大递归层级(栈溢出)
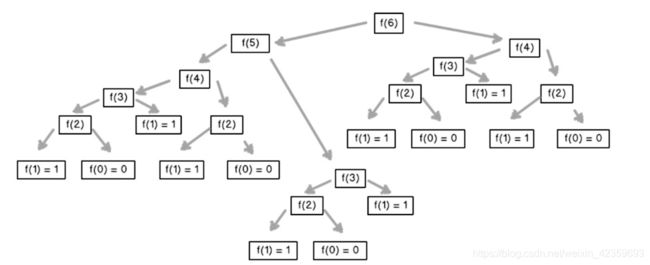
F(6)的递归层级剖析
- 复杂度是
O(2^n),虽然层级近似2^6。 - 有大量的重复子操作,
F(3)有三次。
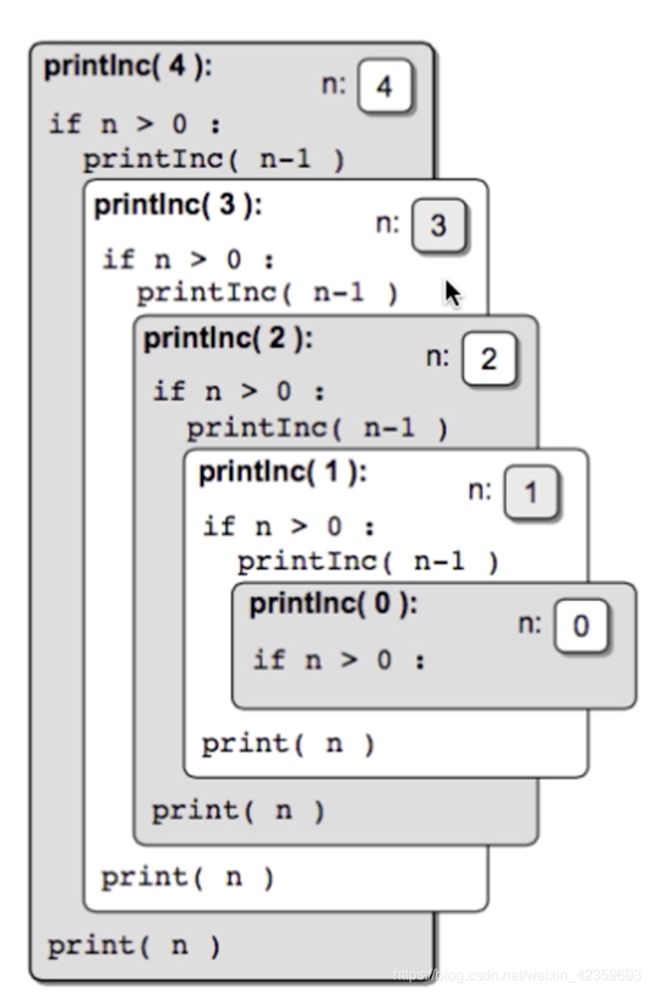
调用栈
递归是基于 调用栈 实现
调用栈的层级剖析
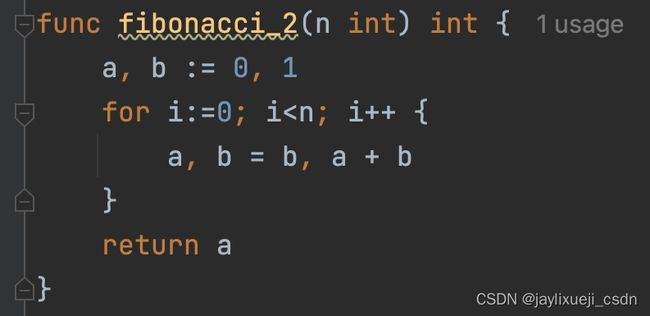
斐波那契数列的优化
- 参考:斐波那契数列的5种python实现写法
- 递归法:O(2^n),大量重复计算,递归深度为1000。
- 递推法:O(n),线性增长。
- 递归优化:缓存中间数,减少重复计算,空间换时间。
golang实现
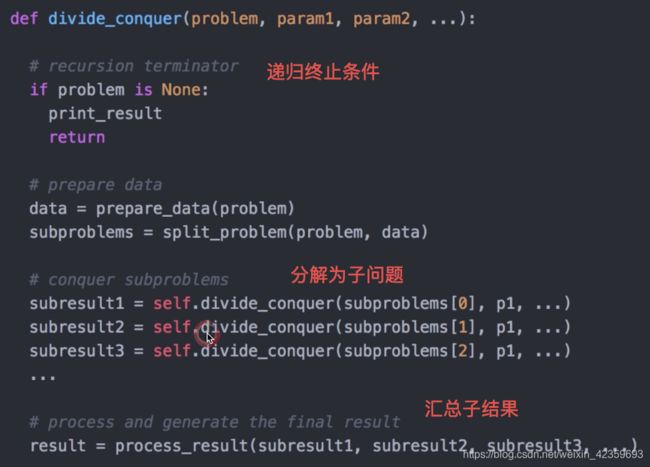
分治(Divide & Conquer)
也是一种递归
字符串变大写
-
解决方案
- 遍历:每个字符均变为大写
- 递归:把第一个字符变大写,剩下放入下一层处理
- 分治:把字符串拆开,然后分别变大写,最后拼接在一起。优势:可以并行,提高速度。
-
仍然存在子问题重复操作的问题
- 动态规划,可以解决
- 子问题记忆,可以解决
分治模板
基础排序算法
冒泡、选择和插入算法的复杂度均为O(N^2)
- 代码:
basic_sort.py
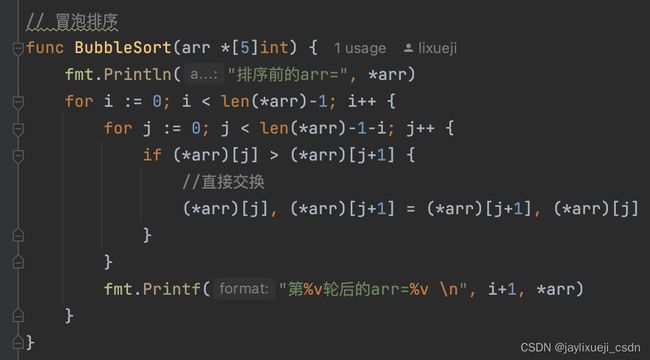
冒泡排序
- 问题背景:10 个小盆友从左到右站成一排,身高不等,老师让其按身高排队。
- 思路分析:
- 第一轮:每次左右比较,高个站右边,9次比较后,最高个换到最右侧
- 第二轮:8次比较后,次高个换到倒数第二个位置
- 第九轮:1次比较
- 代码示例

- 排序过程:
# 不断把大元素挤到右侧
第1轮:[46, 39, 12, 73, 33, 99, 6, 51, 53, 38]
第2轮:[39, 12, 46, 33, 73, 6, 51, 53, 38, 99]
第3轮:[12, 39, 33, 46, 6, 51, 53, 38, 73, 99]
第4轮:[12, 33, 39, 6, 46, 51, 38, 53, 73, 99]
第5轮:[12, 33, 6, 39, 46, 38, 51, 53, 73, 99]
第6轮:[12, 6, 33, 39, 38, 46, 51, 53, 73, 99]
第7轮:[6, 12, 33, 38, 39, 46, 51, 53, 73, 99]
第8轮:[6, 12, 33, 38, 39, 46, 51, 53, 73, 99]
第9轮:[6, 12, 33, 38, 39, 46, 51, 53, 73, 99]
golang实现
参考视频:尚硅谷-golang-冒泡排序
- 代码:BubbleSort/main.go
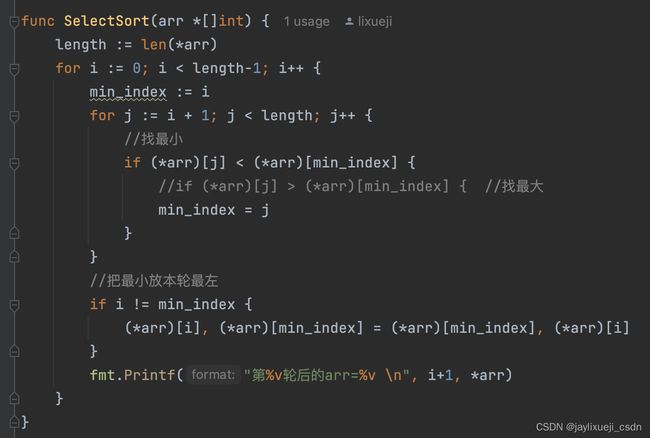
选择排序
- 问题背景:同样10个身高不等的小朋友,按身高排队
- 思路分析:
- 从第一个开始,从头到尾找一个个头最小的小盆友,然后把它和第一个小盆友交换。
- 然后从第二个小盆友开始采取同样的策略,这样一圈下来小盆友就有序了。
- 代码示例

- 排序过程:
# 不断找小元素插入左侧
第1轮:[6, 39, 12, 73, 33, 99, 46, 51, 53, 38]
第2轮:[6, 12, 39, 73, 33, 99, 46, 51, 53, 38]
第3轮:[6, 12, 33, 73, 39, 99, 46, 51, 53, 38]
第4轮:[6, 12, 33, 39, 73, 99, 46, 51, 53, 38]
第5轮:[6, 12, 33, 39, 46, 99, 73, 51, 53, 38]
第6轮:[6, 12, 33, 39, 46, 51, 73, 99, 53, 38]
第7轮:[6, 12, 33, 39, 46, 51, 53, 99, 73, 38]
第8轮:[6, 12, 33, 39, 46, 51, 53, 73, 99, 38]
第9轮:[6, 12, 33, 39, 46, 51, 53, 73, 99, 38]
golang实现
参考视频:尚硅谷-golang-选择排序
- 代码:SelectSort/main.go
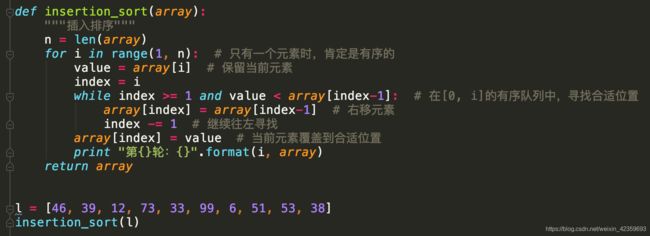
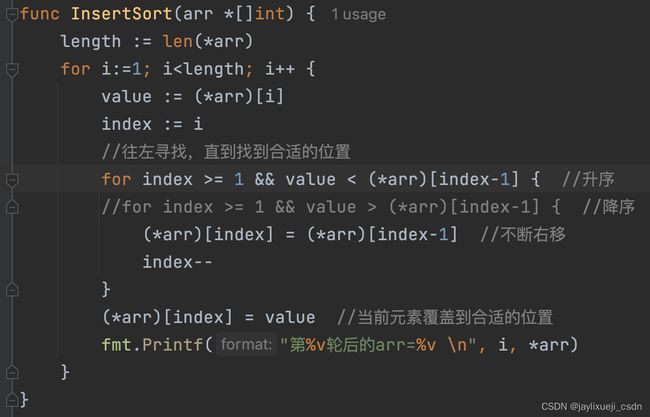
插入排序
-
问题背景:同样10个身高不等的小朋友,按身高排队
-
思路分析:
- 第一次,第二个小朋友与第一个进行比较并排序
- 第二次,第三个小朋友 与 前2个(前2个已有序)比较,并放入合适的位置
- 第十次抽取并插入新队,即得到有序队列
-
排序过程:
# 不断把新元素放到已经有序的数组中
第1轮:[39, 46, 12, 73, 33, 99, 6, 51, 53, 38]
第2轮:[12, 39, 46, 73, 33, 99, 6, 51, 53, 38]
第3轮:[12, 39, 46, 73, 33, 99, 6, 51, 53, 38]
第4轮:[12, 33, 39, 46, 73, 99, 6, 51, 53, 38]
第5轮:[12, 33, 39, 46, 73, 99, 6, 51, 53, 38]
第6轮:[6, 12, 33, 39, 46, 73, 99, 51, 53, 38]
第7轮:[6, 12, 33, 39, 46, 51, 73, 99, 53, 38]
第8轮:[6, 12, 33, 39, 46, 51, 53, 73, 99, 38]
第9轮:[6, 12, 33, 38, 39, 46, 51, 53, 73, 99]
golang实现
参考视频:尚硅谷-插入排序
高级排序算法
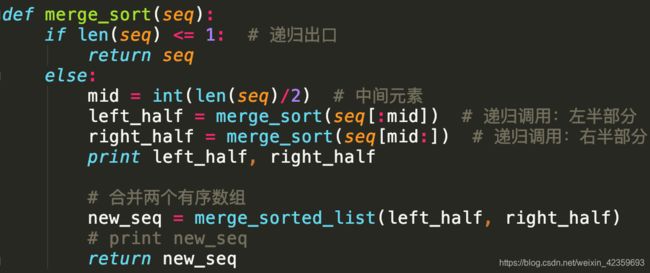
分治法与归并排序
- 时间复杂度:
O(n logn)(不忽略常数项为:O(cn logn + cn)) - 代码示例:
merge_sort.py - 基本思路:归并排序把数组递归成只有单个元素的数组,之后再不断两两 合并,最后得到一个有序数组。
分治法
[46, 39, 12, 73, 33, 99, 6, 51, 53, 38]
↓
[46, 39, 12, 73, 33] [99, 6, 51, 53, 38]
↓ ↓
[46, 39] [12, 73, 33] [99, 6] [51, 53, 38]
↓ ↓ ↓ ↓
[46] [39] [12] [73, 33] [99] [6] [51] [53, 38]
↓ ↓
[73] [33] [53] [38]
归并两个有序数组
A = [1, 3, 5, 7, 9, 11]
B = [0, 2, 8, 9, 11, 15, 16, 17]
# 如何得到有序的 new_seq ?
[46] [39] [12] [73] [33] [99] [6] [51] [53] [38]
↓ ↓ ↓ ↓ ↓ ↓
[39, 46] ↓ [33, 73] [6, 99] ↓ [38, 53]
↓ ↓ ↓ ↓
↓ [12, 33, 73] ↓ [38, 51, 53]
↓ ↓
[12, 33, 39, 46, 73] [6, 38, 51, 53, 99]
↓
[6, 12, 33, 38, 39, 46, 51, 53, 73, 99]
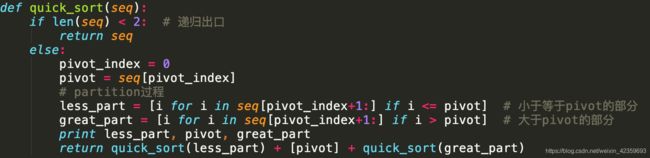
快速排序
-
代码示例:
quick_sort.py -
时间复杂度:
O(n*logn) -
很多程序语言的内置排序都有它的影子。
-
快排也是一种分而治之(divide and conquer)的策略
-
快速排序的基本步骤:
- 选择基准值 pivot 将数组分成两个子数组:小于基准值的元素和大于基准值的元素。这个过程称之为 partition
- 对这两个子数组进行快速排序。
- 合并结果
-
快速排序过程详解
# 分治
[46, 39, 12, 73, 33, 99, 6, 51, 53, 38]
⬇️
[39, 12, 33, 6, 38] 46 [73, 99, 51, 53]
⬇️ ⬇️
[12, 33, 6, 38] 39 [] [51, 53] 73 [99]
⬇️ ⬇️
[6] 12 [33, 38] [] 51 [53]
⬇️
[] 33 [38]
# 然后,合并
-
缺陷:
- less_part和great_part需要额外的存储空间
- partition操作每次都要两次遍历整个数组
-
inplace原地排序,来实现parition操作
-
代码示例:优化后的快排(原地排序,partition只遍历一遍数组)
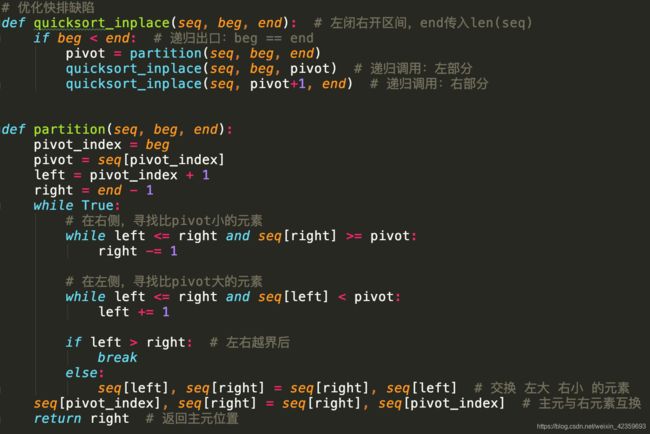
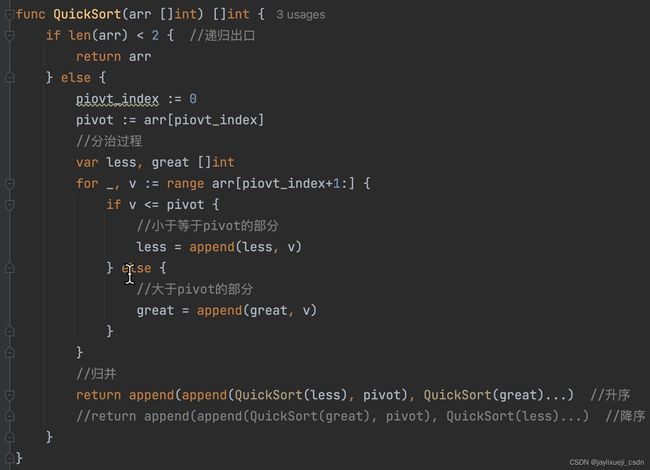
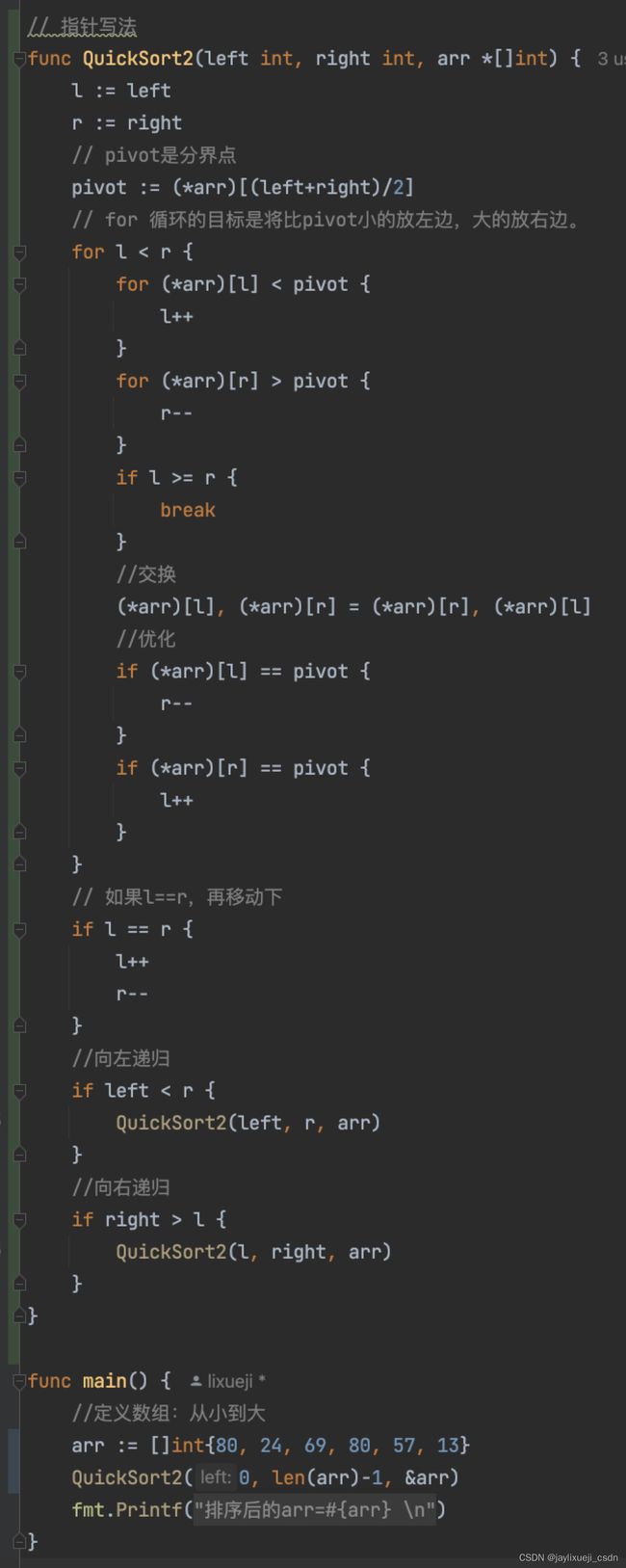
golang实现
使用归并,不是指针
使用指针
参考视频:尚硅谷-快速排序
- 效率高
树
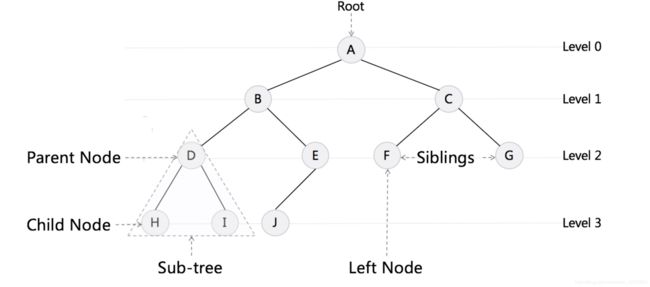
基本概念
-
树状结构是对 链表的进化。
-
树(Tree)
二叉树
Binary Tree
如何构建树节点
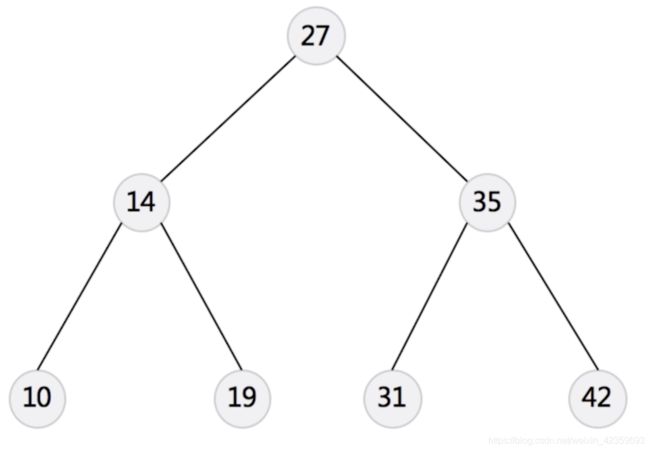
二叉搜索树
工程中常用二叉搜索树
-
二叉搜索树(Binary Search Tree),又称二叉查找树、有序二叉树(Ordered Binary Tree)。
-
排序二叉树(Sorted Binary Tree)是指一棵空树或者具有下列性质的二叉树。
- 左子树上所有节点的值均小于它的根节点的值
- 右子树上所有节点的值均大于它的根节点的值
- Recursively,左、右子树也分别为二叉搜索树
-
查找数据的复杂度为:
O(logN) -
性能优化:当二叉搜索树的性能退化时,可以打乱并重构为新的二叉搜索树。
-
进化数据结构:前三种最差情况也为
O(logN)- 红黑树
- Splay树
- AVL树
- KD树
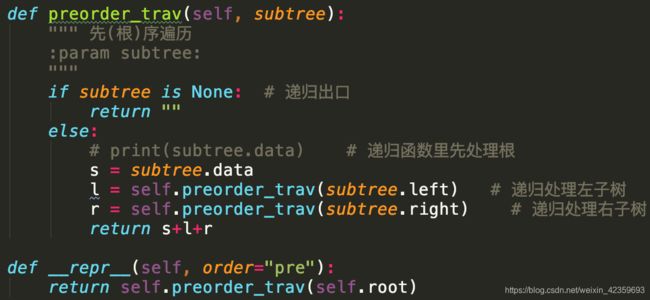
二叉树的遍历
-
三种遍历方式:
- 前序(Pre-order):根-左-右
- 中序(In-order):左-根-右
- 后序(Post-order):左-右-根
-
实际工程使用:
- 深度优先
- 广度优先
- 搜索
遍历顺序
构建二叉树的代码实现
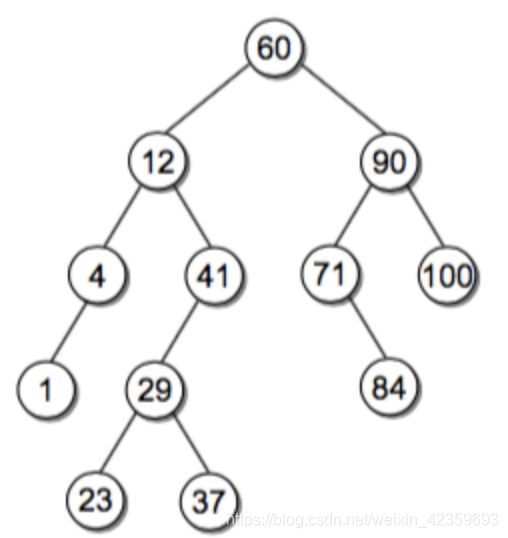
二叉查找树(Binary Search Tree, BST)的代码实现
BST构建
BST操作
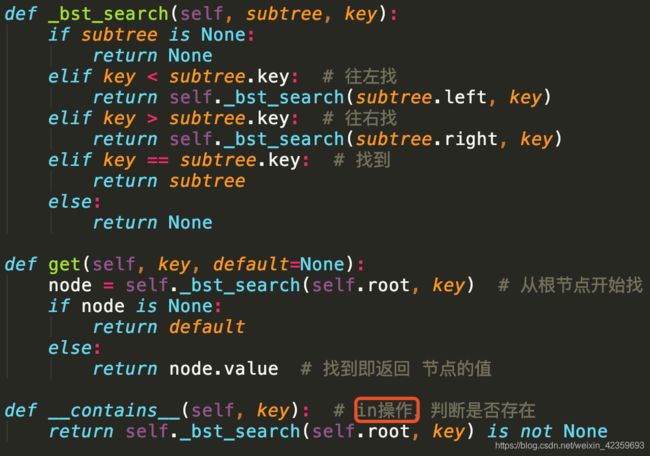
查找
- 按
key在二叉搜索树中查找
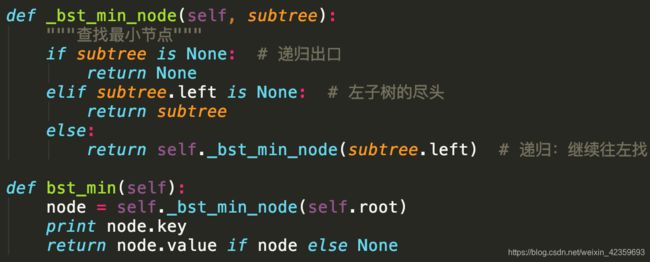
查找最小/大节点
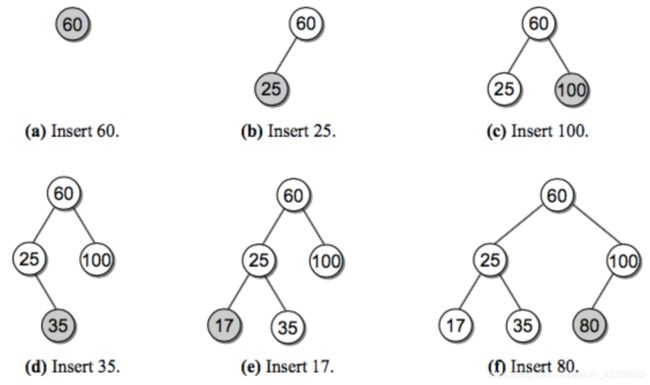
插入
删除
-
删除节点有三种情况:
- 节点是叶节点(无子节点)
- 节点有一个孩子(有一个子节点)
- 节点有两个孩子(有两个子节点)
-
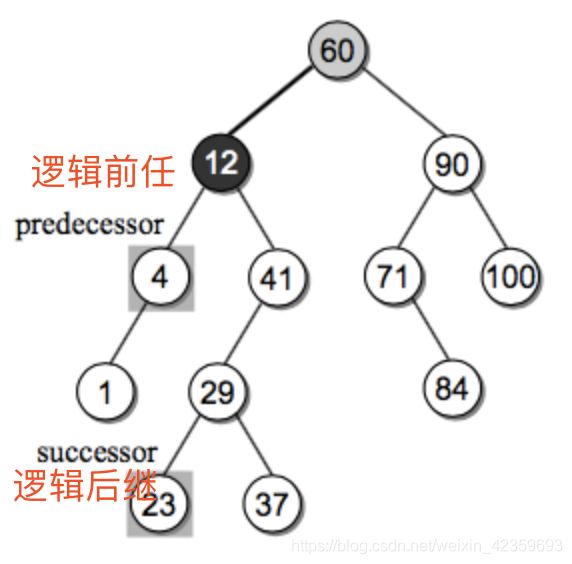
有一个子节点:删除有一个孩子的节点时,我们拿掉需要删除的节点,之后把它的父亲指向它的孩子就行,因为根据 BST 左子树都小于节点,右子树都大于节点的特性,删除它之后这个条件依旧满足。

-
有两个子节点:
-
代码实现:略
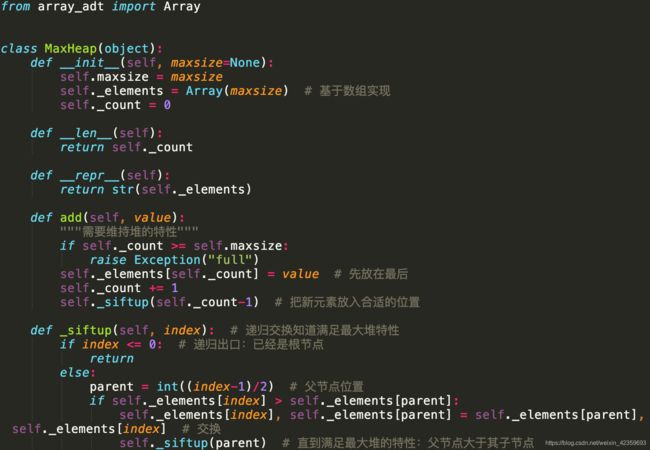
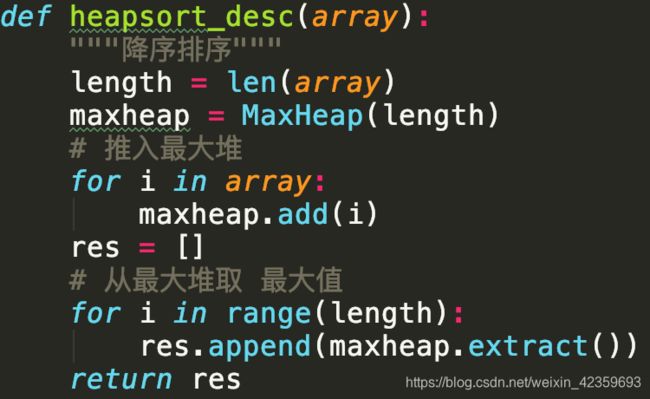
堆(heap)
- 时间复杂度为
O(nlogn)
堆的概念介绍
-
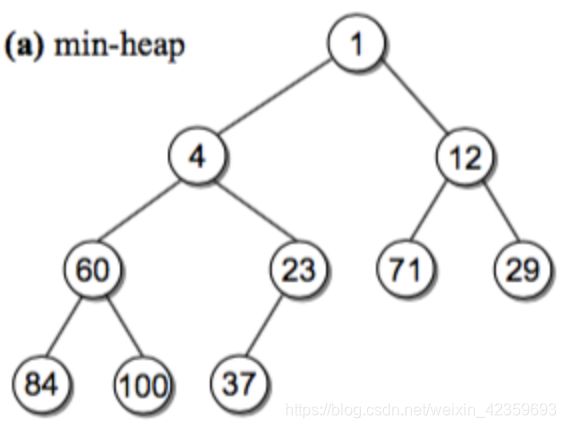
堆是一种完全二叉树,有最大堆和最小堆两种。
-
最大堆: 对于每个非叶子节点 V,V 的值都比它的两个孩子大,称为 最大堆特性(heap order property) 最大堆里的根总是存储最大值,最小的值存储在叶节点。
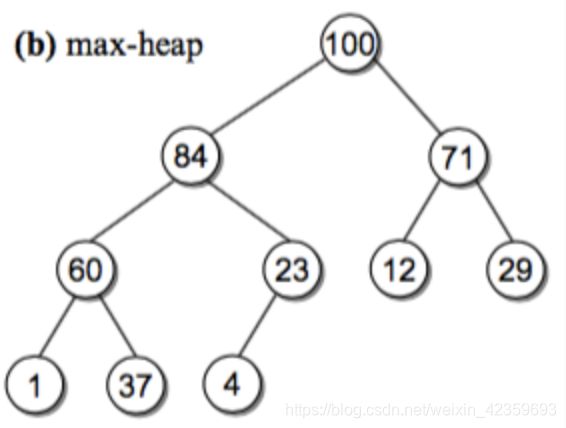
堆的表示
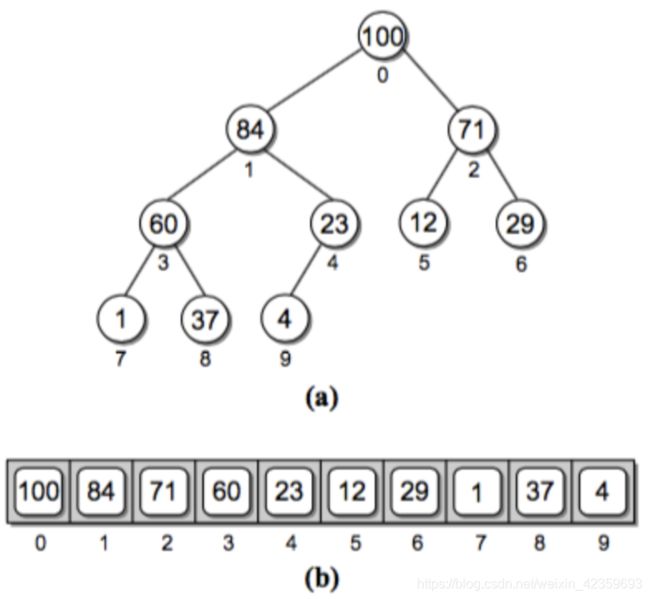
- 基于 数组 实现堆。
- 对于数组里的一个下标 i,我们可以得到它的父亲和孩子的节点对应的下标:
parent = int((i-1) / 2) # 取整
left = 2 * i + 1
right = 2 * i + 2
- 超出下标表示没有对应的孩子节点。
堆的操作
- 基于
array_adt.py实现
插入新节点
删除根节点
- 获取并移除根节点,即删除最大堆的最大值。需要sift-down操作
- sift-down函数:把根节点值移除,把最后一个节点复制到根节点位置,逐层(递归)比较该节点与孩子节点的值,如果孩子值更大 则 该节点与孩子节点 互换,直到满足该节点比孩子大,即满足最大堆特性。

堆排序
二分查找
线性查找
- 线性查找:从头找到尾,直到符合条件了就返回。
number_list = [0, 1, 2, 3, 4, 5, 6, 7]
def linear_search(value, iterable):
for index, val in enumerate(iterable):
if val == value:
return index
return -1
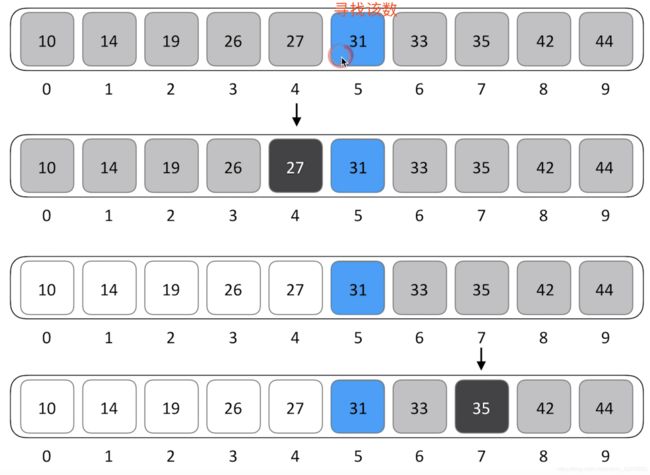
什么是二分查找(Binary Search)
-
前提条件:
- 只能在有序(递增/递减)的数组中实现
- 数组必须存在上下界
- 能通过索引访问
-
时间复杂度:
O(logN) -
缺点:必须是有序数组
代码模板
二分查找详细过程
相关模块
- bisect模块
- itertools模块和常见的几个函数(takewhile, dropwhile, from_iterable, count, tee)