数据结构与算法——归并排序
本专栏是学习王争老师的《数据结构与算法之美》的学习总结,详细内容可以去学习王争老师的专栏,希望大家都能够有所收获。同时也欢迎大家能够与我一起交流探讨!
冒泡排序、插入排序、选择排序三种排序算法的时间复杂度都是O(n^2),适用于小规模数据的排序。
归并排序与快速排序这两种算法适合大规模的数据排序,比上述三种排序算法更常用。
归并排序的原理
归并排序的核心思想:如果要排序一个数组,先把数组从中间分成前后两部分,然后对前后两部分分别排序,再将排好序的两个部分合并在一起,这样整个数组就都有序了。
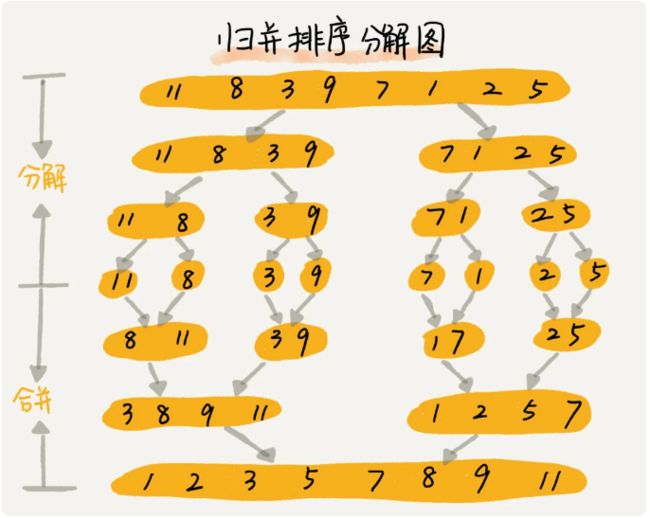
归并算法使用的就是分支思想。分治,顾名思义,就是分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。
分支思想与递归思想类似,分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想,递归是一种编程技巧,这两者并不冲突。
如果用递归代码实现归并排序?
递归代码的编写技巧就是分析得出递推公式,然后找到终止条件,最后将递推公式翻译成递归代码。
要想写出归并排序的代码,首先需要写出归并排序的递推公式。
递推公式:
merge_sort(p…r) = merge(merge_sort(p…q), merge_sort(q+1…r))
终止条件:
p >= r 不用再继续分解
上述递推公式中,merge_sort(p…r) 表示,给下标从 p 到 r 之间的数组排序。将这个排序问题转换为两个子问题,merge_sort(p…q) 和 merge_sort(q+1…r),其中下标 q 等于 p 和 r 的中间位置,即q = (p+r)/2。当下标从 p 到 q 和从 q+1 到 r 这两个子数组都排好序之后,再将两个有序的子数组合并在一起,这样下标从 p 到 r 之间的数据就也排好序了。Java代码如下图所示:
public static void main(String[] args) {
int[] arr = { 49, 38, 65, 97, 76, 13, 27, 50 };
MergeSort mergeSort = new MergeSort();
mergeSort.mergeSort(arr, 0, arr.length-1);
}
public void mergeSort(int[] arr, int start, int end) {
// 当子序列中只要有一个元素时结束递归
if (start < end) {
int mid = (start + end) / 2; // 划分子序列
mergeSort(arr, start, mid); // 对左侧子序列进行递归排序
mergeSort(arr, mid+1, end); // 对右侧子序列进行递归排序
merge(arr, start, mid, end); // 合并
}
}
上述伪代码中,merge(A[p…r], A[p…q], A[q+1…r]) 这个函数的作用就是,将已经有序的 A[p…q]和 A[q+1…r]合并成一个有序的数组,并且放入 A[p…r]。
两个有序数组合并为一个有序数组的过程如何?申请一个临时数组tmp,大小与A[p…r]相同。用两个下标 i 和 j,分别指向 A[p…q]和 A[q+1…r]的第一个元素。比较两个元素A[i]和 A[j]:
- 如果 A[i] <= A[j],就把 A[i]放入到临时数组 tmp,并且 i 后移一位,
- 反之,将 A[j]放入到数组 tmp,j 后移一位。
继续上述比较过程,直到其中一个子数组中的所有数据都放入临时数组中,再把另一个数组中的数据依次加入到临时数组的末尾,这时临时数组中存储的就是两个子数组合并之后的结果。最后再把临时数组 tmp 中的数据拷贝到原数组 A[p…r]中。

上述实现过程的Java代码如下:
// 两路归并算法,两个排好序的子序列合并为一个子序列
public void merge(int[] arr, int left, int mid, int right) {
// 定义一个辅助数组
int[] temp = new int[arr.length];
// p1、p2是检测指针,store是存放指针
int p1= left;
int p2 = mid + 1;
int store = left;
// 合并两个排序好的子序列
while (p1 <= mid && p2 <= right) {
if (arr[p1] <= arr[p2]) {
temp[store++] = arr[p1++];
} else {
temp[store++] = arr[p2++];
}
}
// 检查左右两边的子序列哪一边还有剩余的元素
while (p1 <= mid) {
temp[store++] = arr[p1++];
}
while (p2 <= right) {
temp[store++] = arr[p2++];
}
// 复制回原数组
for (int i = left; i <= right; i++) {
arr[i] = temp[i];
}
}
归并排序的性能分析
归并排序是稳定的排序算法吗?
归并排序是不是稳定的排序算法,取决于merge函数,即两个有序子数组合并成一个有序数组的那部分代码。
在合并过程中,如果 A[p…q]和 A[q+1…r]之间有值相同的元素,可以先将 A[p…q]中的元素加入到临时数组tmp数组,这样保证值相同的元素,在合并前后的顺序不变,因此,归并排序是一个稳定的排序算法。
归并排序的时间复杂度是多少?
归并排序涉及递归,递归的适用场景是一个问题 a 可以分解为多个子问题 b、c,那求解问题 a 就可以分解为求解问题 b、c。问题 b、c 解决之后,我们再把 b、c 的结果合并成 a 的结果。
如果定义求解问题 a 的时间是 T(a),求解问题 b、c 的时间分别是 T(b)、T©,则可以得到这样的递推关系式:
T(a) = T(b) + T(c) + K
其中 K 等于将两个子问题 b、c 的结果合并成问题 a 的结果所消耗的时间。
从上诉分析中,可以得到一个重要结论:不仅递归求解的问题可以写成递推公式,递归代码的时间复杂度也可以写成递推公式。
通过上述公式,分析归并归并排序的时间复杂度:
假设对 n 个元素进行归并排序需要的时间是 T(n) ,那分解成两个子排序的时间都是 T(n/2)。merge()函数合并两个有序子数组的时间复杂度是O(n)。所以,通过上面的公式,归并排序的时间复杂度计算公式如下:
T(1) = C; n=1时,只需要常量级的执行时间,所以表示为C。
T(n) = 2*T(n/2) + n; n>1
进一步计算
T(n) = 2*T(n/2) + n
= 2*(2*T(n/4) + n/2) + n = 4*T(n/4) + 2*n
= 4*(2*T(n/8) + n/4) + 2*n = 8*T(n/8) + 3*n
= 8*(2*T(n/16) + n/8) + 3*n = 16*T(n/16) + 4*n
......
= 2^k * T(n/2^k) + k * n
......
通过这样一步一步分解推导,可以得到 T(n) = 2kT((n/2)k) + k * n。当 T(n/2k)=T(1) 时,也就是 (n/2)k=1,我们得到 k=log2(n) 。
将 k 值代入上面的公式,得到 T(n)=Cn+nlog2n 。如果用大 O 标记法来表示的话,T(n) 就等于 O(nlogn)。所以归并排序的时间复杂度是 O(nlogn)。
从上述分析可以看出,归并排序的执行效率与要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均情况,时间复杂度都是 O(nlogn)。
归并排序的空间复杂度?
归并排序的时间复杂度任何情况下都是 O(nlogn),看起来非常优秀。但是,归并排序并没有像快排那样,应用广泛,这是为什么呢?因为它有一个致命的“弱点”,那就是归并排序不是原地排序算法。
归并排序的合并函数merge在合并两个有序数组为一个有序数组时,需要借助额外的存储空间。
实际上,递归代码的空间复杂度并不能像时间复杂度那样累加。尽管每次合并操作都需要申请额外的内存空间,但在合并完成之后,临时开辟的内存空间就被释放掉了。在任意时刻,CPU 只会有一个函数在执行,也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小,所以空间复杂度是 O(n)。
总结
1、归并排序的核心思想,先将数组从中间分成前后两部分,然后对前后两部分分别排序,再将排序好的两部分合并在一起,使得整个数组有序。
2、归并排序使用的是分治思想。分而治之,将一个大问题分解成小的子问题来解决。小的子问题解决了,大问题也就解决了。
3、分治算法一般都是用递归来实现的。分治是一种解决问题的处理思想,递归是一种编程技巧,这两者并不冲突。
4、在merge()函数合并的过程中,如果 A[p…q]和 A[q+1…r]之间有值相同的元素,可以先把 A[p…q]中的元素放入 tmp 数组。保证值相同的元素在合并前后的先后顺序不变。因此,归并排序是一个稳定的排序算法。
5、归并排序的执行效率与要排序的原始数组的有序程度无关,所以其时间复杂度是非常稳定的,不管是最好情况、最坏情况,还是平均情况,时间复杂度都是 O(nlogn)。
6、归并排序尽管每次合并操作都需要申请额外的内存空间,但在合并完成之后,临时开辟的内存空间就被释放掉了。在任意时刻,CPU 只会有一个函数在执行,也就只会有一个临时的内存空间在使用。临时内存空间最大也不会超过 n 个数据的大小,所以空间复杂度是 O(n)。