数据结构与算法 —— 归并排序
今天讲的内容是归并排序,为了比较容易的理解归并排序,我们首先看一道leetcode的算法题,通过该题的解题思路,会让我们更加容易的理解归并排序的思想。
开篇问题
这个题的解题思路其实就是归并排序的merge的过程。首先让我们先解这道题,便于后面更好的理解归并排序的思想。
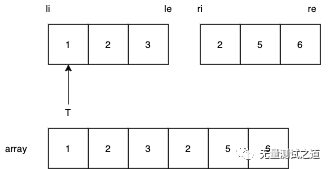
首先我绘制了一张图,接下来我们通过上图来理解这道题的解题思路。
在开始之前,我先解释下上图的变量的含义:我们定义一个数组array = nums1 + nums2,然后定义指针T指向nums1的第一个元素的位置;此外,我们还定义了li(即left_index)和le(left_endIndex)以及ri、re。
思路:
通过实际的数据,我们来走一遍流程,暂时不用去考虑特殊情况,理解好整体的思路后再去考虑细节和特殊情况。
-
通过比较nums1[li] 和nums2[ri] 的大小,如果nums1[li] > nums2[ri],则array[T] = nums2[ri],然后ri++, T++; 如果nums1[li] < nums2[ri],则array[T] = nums2=1[li],然后li++, T++;
-
一直重复上述过程,直到li > le 或者 ri > re 就结束
实际的数据走一遍流程:
1. 1 < 2 , T = 0,所以 array[T] = 1, li++, T++
2. 2 == 2, T = 1,所以 array[T] = 2, li++, T++
3. 3 > 2 , T = 2,所以 array[T] = 2, ri++, T++
4. 3 < 5 , T = 3,所以 array[T] = 3, li++, T++
5. 由于左边的数组即num1已经遍历完成,并且nums2是有序的,所以直接将nums2数组的值覆盖array后面的值即可
6. 反之如果右边的数据即nums2先遍历完成,则将nuns1数组的值覆盖进去即可
7. 完成
实现代码:
func merge(_ nums1: inout [Int], _ m: Int, _ nums2: [Int], _ n: Int) {
var array = [Int](repeating: 0, count: (m + n))
for i in 0 ..< m {
array[i] = nums1[i]
}
for i in 0 ..< n {
array[i+m] = nums2[i]
}
var li = 0; let le = m;
var ri = 0; let re = n;
var t = 0
while li < le {
if ri < re && nums1[li] > nums2[ri] {
array[t] = nums2[ri]
t += 1
ri += 1
}else {
array[t] = nums1[li]
t += 1
li += 1
}
}
print(array)
}归并排序
归并排序(Merge Sort)是建立在归并操作上的一种有效、稳定的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并。
其算法执行流程就是:
-
不断的将当前序列平均分割成2个子序列,直到不能再分割(序列中只剩一个元素)
-
不断的将2个子序列合并成一个有序序列,直到最终只剩下一个有序序列
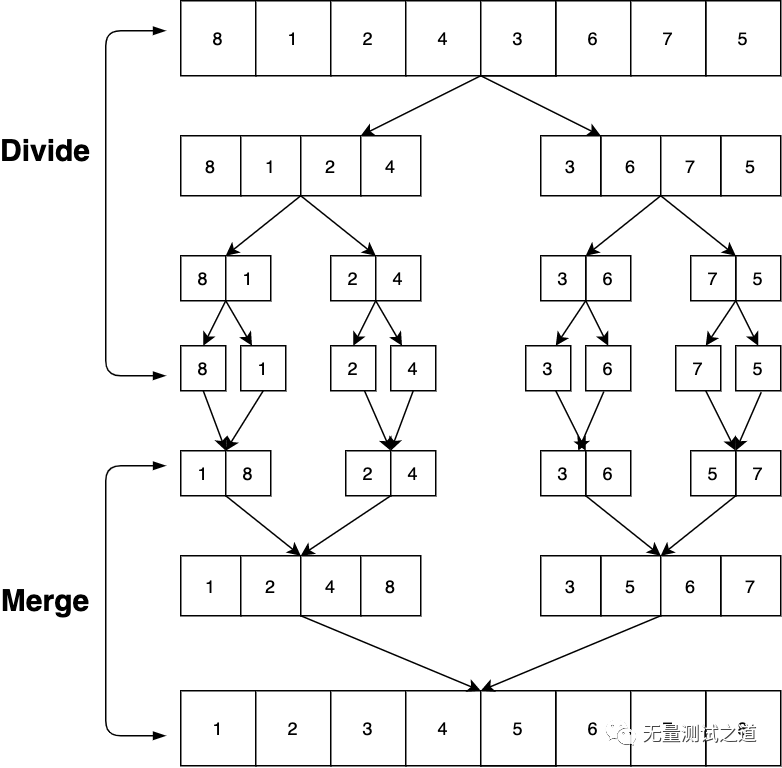
对应如下图:
上述两个操作对应为:divide 和merge;divide操作就是将序列进行分割,分割到单位1;merge操作的就是将序列进行合并,直到最后只剩下一个序列。我们看merge的倒数第二个操作,是不是就是本文的开篇问题,即将2个有序的数组进行合并。
代码理解
因为归并排序中主要用到的就是分治的思想,包含递归的编程技巧,所以我打算先贴代码再来讲解其实现思路.
现实场景:给一个乱序的数组array = [3,5,6,1,2,7,8,4,9,10] ,使用归并排序进行排序
class Mergesort: Sort {
private var leftArray = [Int]()
private var array = [Int]()
override func sort( array: inout [Int]) -> [Int] {
self.array = array
self.leftArray = [Int](repeating: 0, count: self.array.count/2)
divide(begin: 0, end: array.count)
return self.array
}
private func divide(begin: Int, end: Int) {
if end - begin < 2 { return }
let mid = (begin + end) >> 1
divide(begin: begin, end: mid)
divide(begin: mid, end: end)
merge(begin: begin, mid: mid, end: end)
}
private func merge(begin: Int, mid: Int, end: Int) {
var li = 0; let le = mid - begin;
var ri = mid; let re = end
var ai = begin
for i in li ..< le {
leftArray[i] = array[begin + i]
}
while li < le {
if ri < re && leftArray[li] > array[ri] {
array[ai] = array[ri]
ai += 1
ri += 1
}else {
array[ai] = leftArray[li]
ai += 1
li += 1
}
}
}
}关于merge操作,我相信,通过开篇问题的讲解,大家在心中大致有一个思路。剩下的就是理解divide操作的实现过程,我们来看divide方法:
private func divide(begin: Int, end: Int) {
if end - begin < 2 { return }
let mid = (begin + end) >> 1
divide(begin: begin, end: mid)
divide(begin: mid, end: end)
merge(begin: begin, mid: mid, end: end)
}-
首先将传过来array进行分割,先分割成 [0--array.count]和array.count/2--array.count]
-
然后将array[0--array.count/2] 和 array[array.count/2--array.count]再进行更细化的分割
-
最后进行merge
提示:看递归代码,你心中要知道它是怎样调的。递归就是多层调用栈,调用栈比较深。具体的可以参考之前的文章,我有比较细致的走过一次递归流程。
总结:
今天开题比较详细地讲解了合并2个有序数组的算法题,并且通过实际的例子走了一遍merge的流程,为后文讲解归并排序做了铺垫。然后通过绘图的形式讲解了归并排序的divide和sort,并且通过代码实现了归并排序算法。最后,也讲解了下divide的递归实现流程。最后的最后,希望读者朋友们通过阅读这篇文章,可以比较通俗易懂的理解归并排序算法。
欢迎关注【无量测试之道】公众号,回复【领取资源】,
Python编程学习资源干货、
Python+Appium框架APP的UI自动化、
Python+Selenium框架Web的UI自动化、
Python+Unittest框架API自动化、
资源和代码 免费送啦~
文章下方有公众号二维码,可直接微信扫一扫关注即可。
备注:我的个人公众号已正式开通,致力于测试技术的分享,包含:大数据测试、功能测试,测试开发,API接口自动化、测试运维、UI自动化测试等,微信搜索公众号:“无量测试之道”,或扫描下方二维码:
![]()
添加关注,让我们一起共同成长!