IEEE 754标准浮点数详解,总结笔记
参考教材:王道计算机组成原理考研复习指导,计算机组成原理-蒋本珊
IEEE 754标准
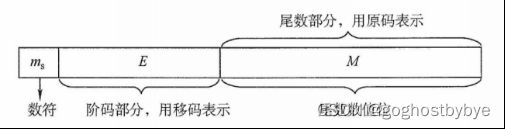
按照IEEE 754标准,浮点数的格式标准如图所示。
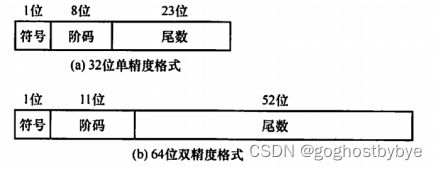
常用的浮点数格式如图
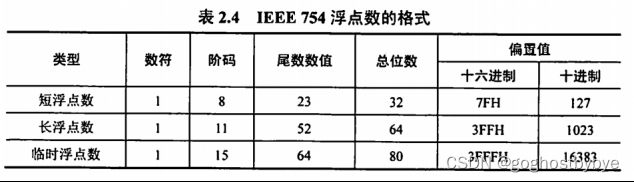
常用的浮点数格式有三类:短浮点数(单精度、float型)、长浮点数(双精度、double型)、临时浮点数。
IEEE 754标准的浮点数(除临时浮点数外),是尾数用采取隐藏位策略的原码表示,且阶码用移码表示的浮点数。
一、阶码
IEEE754标准的浮点数用移码表示阶码,其中移码的偏置值(偏移量)不再是一般移码定义的偏置值([x]移 = 2n + x,其中x为二进制真值,n为真值x的位数,移码的位数为n + 1)。偏移量等于2n - 1,即n个1。
即阶码用移码表示为
E = [ x ]移 = 2^n - 1 + x = 11...1 + x
对于短浮点数,偏置值为127(7个1); 对于长浮点数,偏置值为1023(10个1)
以短浮点数为例,最高位为数符位;其后是8位阶码,以2为底,用移码表示,阶码的偏置值为128-1 = 127; 其后23位是原码表示的尾数数值位。
二、尾数
对于规格化的二进制浮点数,数值的最高位总是“1”。为了能使尾数多表示一位有效位,将这个“1”隐含,因此尾数数值实际上是24位。隐含的“1”是一位整数。在浮点格式中表示的23位尾数是纯小数。
注意:IEEE标准浮点数已经有一位数符表示浮点数的符号,所以尾数不需要加符号位,尾数规格化和前一节规格化浮点数尾数规格化不一样。
例如,(12)10 =(1100)2,将它规格化后结果为1.1x23,其中整数部分的“1”将不存储在23位尾数内。
注意:短浮点数与长浮点数都采用隐含尾数最高数位的方法,因此可多表示一位尾数。而临时浮点数又称扩展精度浮点数,无隐含位。
三、规格化浮点数
IEEE 754标准中,规格化的短浮点数的真值为
(-1)^S x 1.M x 2^(E-127)
规格化长浮点数的真值为
(-1)^S x 1.M x 2(E-1023)
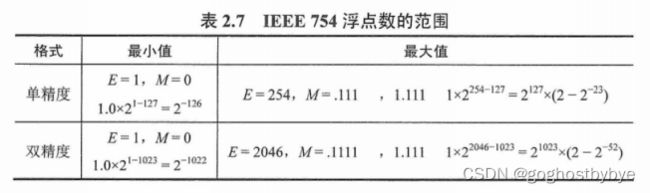
式中,s=0表示正数,s= 1表示负数;短浮点数E的取值为1~254 (8位表示),M为23位,共32位;长浮点数E的取值为1~2046 (11 位表示),M为52位,共64位。
IEEE 754标准浮点数的范围见表2.7。
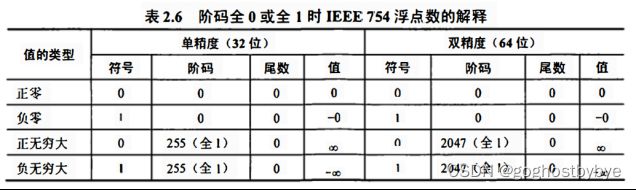
对于IEEE 754格式的浮点数,阶码全0或全1时,有其特别的解释,如表2.6所示。
1)全0阶码全0尾数: +0/-0。零的符号取决于数符S,一般情况下+0和-0是等效的。
2)全1阶码全0尾数: +∞/-∞。+∞在数值上大于所有有限数,-∞则小于所有有限数。
引入无穷大数的目的是,在计算过程出现异常的情况下使得程序能继续进行下去。
四、例题
例1
将(100.25)10转化成短浮点数格式
1.把十进制数转化为二进制数
(100.25)10 = (1100100.01)2
2.规格化二进制数
1100100.01 = 1.10010001 × 2^6
3.计算出阶码的移码(偏置值 + 阶码真值,二者都是二进制数)
偏置值:27 - 1 = 1111111 阶码真值:110
移码:1111111 + 110 = 10000101
注意:也可以将两个二进制数转化为十进制数相加
偏置值:127 阶码真值:6
移码:127 + 6 = (133)10 = (10000101)2
4.以短浮点数格式存储
符号位:0
阶码:10000101
尾数:10010001,000000000000000(不足23位在后面补0,逗号实际隐含)
所以,短浮点数为:0;10000101;10010001,000000000000000
例2
把浮点数C1C90000H转化成十进制数
1.将十六进制数转化为二进制数,并分离出符号位、阶码、尾数
C1C90000H = 1;10000011;1001001,0000000000000000
符号位:1
阶码:10000011
尾数:1001001,0000000000000000
2.计算出阶码真值(用阶码表示的移码 - 偏置值)
10000011 - 1111111 =(100)2= (4)10
3.写出这个数的规格化二进制数形式
1.1001001 × 2^4
4.转化为非规格化二进制数格式
11001.001
5.转化为十进制数,并加上符号位
(11001.001)2=(25.125)10
所以,该浮点数的十进制数为-25.125