【代码随想录算法训练营14期】-Day15 第六章 二叉树 part02
今日内容
● 层序遍历 10
● 226.翻转二叉树
● 101.对称二叉树 2
第六章 二叉树 part02
- 层序遍历
-
- 102. 二叉树的层序遍历
-
- 1.解题思路
- 2.代码
- 107. 二叉树的层序遍历 II
-
- 1.解题思路
- 2.代码
- 199. 二叉树的右视图
-
- 1.解题思路
- 2.代码
- 637. 二叉树的层平均值
-
- 1.解题思路
- 2.代码
- 429. N 叉树的层序遍历
-
- 1.解题思路
- 2.代码
- 515. 在每个树行中找最大值
-
- 1.解题思路
- 2.代码
- 116. 填充每个节点的下一个右侧节点指针
- 117. 填充每个节点的下一个右侧节点指针 II
-
- 1.解题思路
- 2.代码
- 104. 二叉树的最大深度
-
- 1.解题思路
- 2.代码
- 111. 二叉树的最小深度
-
- 1.解题思路
- 2.代码
- 226.翻转二叉树 (优先掌握递归) 
-
- 1.解题思路
-
- 2.代码
- 101. 对称二叉树
-
- 1.解题思路
-
- 2.代码
- 总结
层序遍历
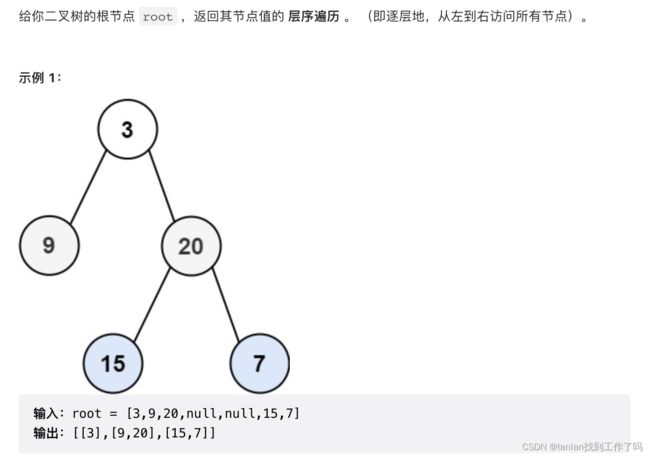
102. 二叉树的层序遍历
1.解题思路
二叉树的层次遍历借用队列,先让根节点入队列,在队列不空的情况下,循环每层元素数量取队头元素,然后让其左右儿子入队列。
2.代码
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int>> ans;
queue<TreeNode*> q;
if(root == nullptr) return ans;
q.push(root);
while(!q.empty()){
vector<int> res;
int n = q.size();
while(n--){
TreeNode* node = q.front();
q.pop();
res.push_back(node->val);
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
ans.push_back(res);
}
return ans;
}
};
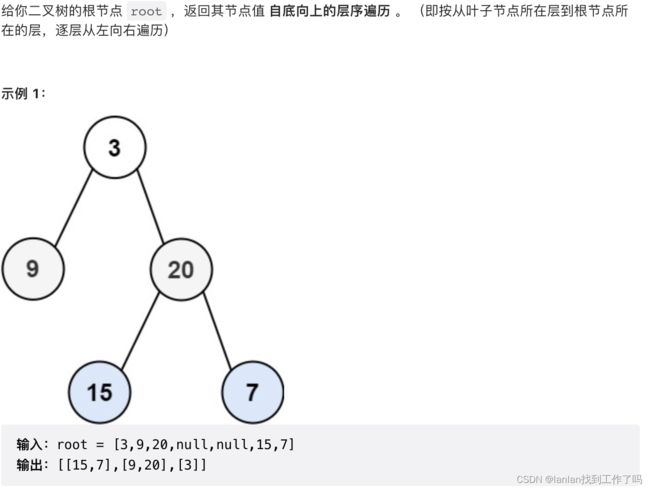
107. 二叉树的层序遍历 II
1.解题思路
二叉树的层次遍历以后将数组反转
2.代码
class Solution {
public:
vector<vector<int>> levelOrderBottom(TreeNode* root) {
vector<vector<int>> ans;
if(root == nullptr) return ans;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
int n = q.size();
vector<int> res;
while(n--){
TreeNode* node = q.front();
res.push_back(node->val);
q.pop();
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
ans.push_back(res);
}
reverse(ans.begin(),ans.end());
return ans;
}
};
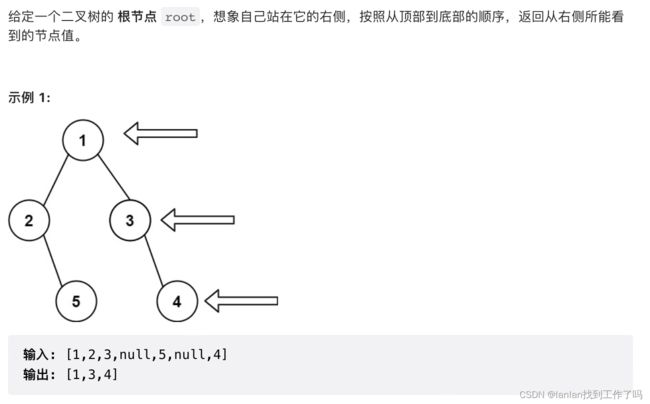
199. 二叉树的右视图
1.解题思路
二叉树的层次遍历时只把每层最后一个节点值记录下来(n==0)。
2.代码
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
//层次遍历每层最后的一个
vector<int> ans;
if(root == nullptr)
return ans;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
int n = q.size();
while(n--){
TreeNode* node = q.front();
q.pop();
if(n == 0)
ans.push_back(node->val);
if(node->left)
q.push(node->left);
if(node->right)
q.push(node->right);
}
}
return ans;
}
};
637. 二叉树的层平均值
1.解题思路
二叉树的层次遍历时只把每层值加和后➗每层数量。
2.代码
class Solution {
public:
vector<double> averageOfLevels(TreeNode* root) {
vector<double> ans;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
int n = q.size();
double res = 0;
for(int i = 0; i < n; i++){
TreeNode* node = q.front();
res += node->val;
q.pop();
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
ans.push_back(res/n);
}
return ans;
}
};
429. N 叉树的层序遍历
1.解题思路
N 叉树的层序遍历就没有左右孩子了,在取出队头值时,size计算cur->children.size()个数,for循环加入其孩子个数入队列。
2.代码
class Solution {
public:
vector<vector<int>> levelOrder(Node* root) {
vector<vector<int>> ans;
if(root == nullptr)
return ans;
queue<Node*> q;
q.push(root);
while(!q.empty()){
vector<int> res;
int n = q.size();
for(int i = 0; i < n; i++){
Node* cur = q.front();
q.pop();
res.push_back(cur->val);
for(int i = 0; i < cur->children.size(); i++){
if(cur->children[i])
q.push(cur->children[i]);
}
}
ans.push_back(res);
}
return ans;
}
};
515. 在每个树行中找最大值
1.解题思路
层次遍历每层res赋初值INT_MIN,每取出队头的值与其比较大小,大就替代res。
2.代码
class Solution {
public:
vector<int> largestValues(TreeNode* root) {
vector<int> ans;
if(!root) return ans;
queue<TreeNode*> q;
q.push(root);
while(!q.empty()){
int n = q.size();
int res = INT_MIN;
while(n--){
TreeNode* node = q.front();
q.pop();
if(res < node->val) res = node->val;
if(node->left) q.push(node->left);
if(node->right) q.push(node->right);
}
ans.push_back(res);
}
return ans;
}
};
116. 填充每个节点的下一个右侧节点指针
117. 填充每个节点的下一个右侧节点指针 II
1.解题思路
层次遍历时去出队头节点pre,弹出该节点,此时队列队头节点即为pre->next,只需要判断n的值,当该层元素数循环到n==0时,为这层最后的节点不需要操作。
2.代码
class Solution {
public:
Node* connect(Node* root) {
if(!root) return root;
queue<Node*> q;
q.push(root);
Node* pre;
while(!q.empty()){
int n = q.size();
while(n--){
pre = q.front();
q.pop();
if(n > 0){
pre->next = q.front();
}
if(pre->left) q.push(pre->left);
if(pre->right) q.push(pre->right);
}
}
return root;
}
};
104. 二叉树的最大深度
1.解题思路
层次遍历可以使用depth记录遍历一层depth++;递归返回条件root为空return 0,递归返回左右孩子深度大的+1(根结底)
2.代码
class Solution {
public:
int maxDepth(TreeNode* root) {
if(!root) return 0;
return max(maxDepth(root->left),maxDepth(root->right)) + 1;
}
};
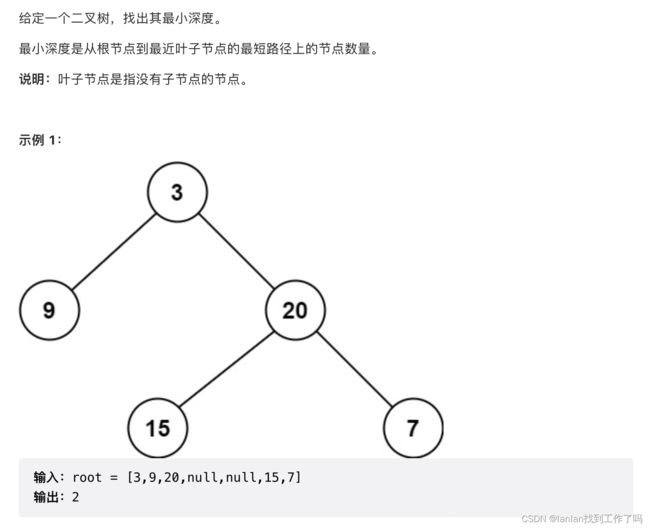
111. 二叉树的最小深度
1.解题思路
这道题的关键是搞清楚递归结束条件
叶子节点的定义是左孩子和右孩子都为 null 时叫做叶子节点 ,
当 root 节点左右孩子都为空时,返回 1
当 root节点左右孩子有一个为空时,返回不为空的孩子节点的深度
当 root 节点左右孩子都不为空时,返回左右孩子较小深度的节点值
2.代码
class Solution {
public:
int minDepth(TreeNode* root) {
if(!root) return 0;
//左右孩子都不为空,返回小的深度min
if(root->left && root->right)
return min(minDepth(root->left),minDepth(root->right)) + 1;
//左右孩子有一个为空,返回不为空的即max
else
return max(minDepth(root->left),minDepth(root->right)) + 1;
}
};
226.翻转二叉树 (优先掌握递归) 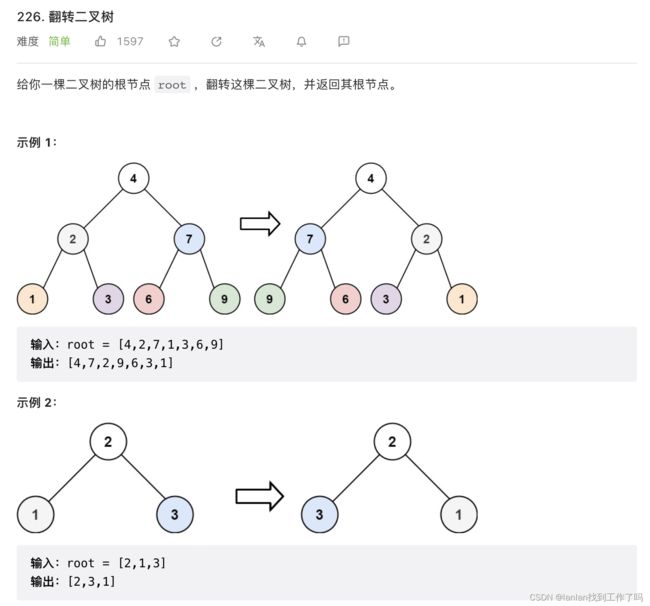
1.解题思路
翻转二叉树,可以使用前序和后序swap,但是不能使用中序,因为使用中序会使右子树不能翻转保持原样。
2.代码
class Solution {
public:
TreeNode* invertTree(TreeNode* root) {
if(!root) return root;
swap(root->left,root->right);
invertTree(root->left);
invertTree(root->right);
return root;
}
};
101. 对称二叉树
1.解题思路
对称二叉树,比较左右子树,对每对对称节点,首先判断节点是否存在,如果其中一个节点为空,其中一个不为空,return false,如果两个为空,即true;再判断val,如果两个节点值不相同,false;如果节点值相同,则继续递归左右子树,由于对称性,一个向左一个向右。
2.代码
class Solution {
public:
bool issame(TreeNode* root,TreeNode* r){
if(root == nullptr && r) return false;
else if(root && r == nullptr) return false;
else if(root == nullptr && r == nullptr) return true;
else if(root->val != r->val) return false;
else
return issame(root->left,r->right) && issame(root->right,r->left);
}
bool isSymmetric(TreeNode* root) {
if(!root) return true;
return issame(root->left,root->right);
}
};
总结
- 层次遍历,使用队列暂存元素,计算每层节点数量,分层遍历节点,每遍历一个节点,存入数组,弹出队列,并把左右非空儿子加入队列;
- 翻转二叉树前后序递归均可
- 对称二叉树,递归检验左右子树,首先判断节点存在性,再判断值相同性。