【Pytorch】Pytorch学习笔记02 - 单变量时间序列 LSTM
目录
- 说明
- 简单神经网络
- LSTM原理
- Pytorch LSTM
-
- 生成数据
- 初始化
- 前向传播方法
- 训练模型
- 自动化模型构建
- 总结
- 参考文献
说明
这篇文章主要介绍如何使用PyTorch的API构建一个单变量时间序列 LSTM。文章首先介绍了LSTM,解释了它们在时间序列数据中的简单性和有效性。然后,文章解释了如何使用前向方法初始化LSTM,包括定义输入和输出形状,训练模型以及自动化模型构建。最后,文章总结了从头构建LSTM所涉及的关键概念和技术。
简单神经网络
假设我们有以下时间序列数据。我们不使用复杂的递归模型,而是将时间序列视为一个简单的输入 - 输出函数:输入是时间,输出是我们测量的任何因变量的值。这本质上只是简化了一个单变量时间序列。
上面概述的问题与时间序列问题的实际顺序建模方法(如LSTM中使用的)之间有什么区别? 不同之处在于解的递归性。在这里,我们只是简单地传入当前时间步长,并希望网络可以输出函数值。然而,在递归神经网络中,我们不仅传递当前输入,还传递先前的输出。通过这种方式,网络可以学习先前函数值与当前函数值之间的依赖关系。在这里,网络无法学习这些依赖关系,因为我们根本没有将之前的输出输入到模型中。
让我们假设我们试图模拟克莱·汤普森伤愈复出后的上场时间。金州勇士队的教练史蒂夫科尔不希望克莱回来,并立即发挥沉重的分钟。相反,他将以每场比赛几分钟的时间开始克莱,并随着赛季的进行增加他被允许上场的时间。我们将成为克莱汤普森的理疗师,我们需要预测克莱每场比赛将上场多少分钟,以确定他的膝盖需要绑多少绷带。
因此,自伤愈复出以来的比赛次数(代表输入的时间步长)是自变量,克莱·汤普森的比赛分钟数是因变量。假设我们观察克莱11场比赛,记录他每场郊游的上场时间,以获得以下数据。。
X = [x for x in range(11)]
y = [1.6*x + 4 + np.random.normal(10, 1) for x in X]
X, y
([0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10],
[8.059610387807004,
11.05288064074008,
11.353963162111054,
13.816355592580631,
14.13887152857681,
15.694474605527,
15.684278885945714,
15.532815595076784,
18.247200671926283,
20.520472619447048,
20.127253834627])
在这里,我们已经生成了每场比赛的分钟数,与回归后的比赛次数呈线性关系。我们将使用9个样本作为训练集,2个样本用于验证。
X_train = X[:9]
y_train = y[:9]
X_val = X[9:]
y_val = X[9:]
我们知道,比赛次数和分钟数之间是线性关系。然而,我们仍然要使用非线性激活函数,因为这是神经网络的全部意义。(否则,这将变成线性回归:线性操作的组合只是一个线性操作。像往常一样,我们使用nn.Sequential来构建一个隐藏层的模型,其中包含13个隐藏神经元。
seq_model = nn.Sequential(
nn.Linear(1, 13),
nn.Tanh(),
nn.Linear(13, 1))
seq_model
>>> Sequential(
(0): Linear(in_features=1, out_features=13, bias=True)
(1): Tanh()
(2): Linear(in_features=13, out_features=1, bias=True)
)
我们现在需要编写一个训练循环,就像我们在使用梯度下降和反向传播来强制网络学习时所做的那样。为了提醒您,每个培训步骤都有几个关键任务:
- 通过将模型应用于训练示例来计算通过网络的前向传递。
- 根据定义的损失函数计算损失,该函数将模型输出与实际训练标签进行比较。
- 通过网络反向传播损失相对于模型参数的导数。这是在使用
.backward().zero_grad()将当前参数梯度用设置为零后,通过调用loss来完成的。 - 通过减去梯度乘以学习率来更新模型参数。这是用
optimiser.step()调用优化器完成的。
def training_loop(n_epochs, optimiser, model, loss_fn, X_train, X_val, y_train, y_val):
for epoch in range(1, n_epochs + 1):
output_train = model(X_train) # forwards pass
loss_train = loss_fn(output_train, y_train) # calculate loss
output_val = model(X_val)
loss_val = loss_fn(output_val, y_val)
optimiser.zero_grad() # set gradients to zero
loss_train.backward() # backwards pass
optimiser.step() # update model parameters
if epoch == 1 or epoch % 10000 == 0:
print(f"Epoch {epoch}, Training loss {loss_train.item():.4f},"
f" Validation loss {loss_val.item():.4f}")
现在,我们需要做的就是实例化所需的对象,包括我们的模型,我们的优化器,我们的损失函数和我们要训练的epoch数量。
optimiser = optim.SGD(seq_model.parameters(), lr=1e-3)
training_loop(
n_epochs = 500000,
optimiser = optimiser,
model = seq_model,
loss_fn = nn.MSELoss(),
X_train = X_train,
X_val = X_val,
y_train = y_train,
y_val = y_val)
>>> Epoch 1, Training loss 422.8955, Validation loss 372.3910
...
Epoch 500000, Training loss 0.0007, Validation loss 299.8014
正如我们所看到的,该模型很可能过度拟合(可以通过许多技术解决,例如正则化,或降低模型参数的数量,或强制执行线性模型形式)。训练损失基本为零。由于我们的因变量存在固有的随机变化,在最后几场比赛中,上场时间逐渐减少,变成一条平坦的曲线,导致模型认为这种关系更像是一条对数而不是一条直线。
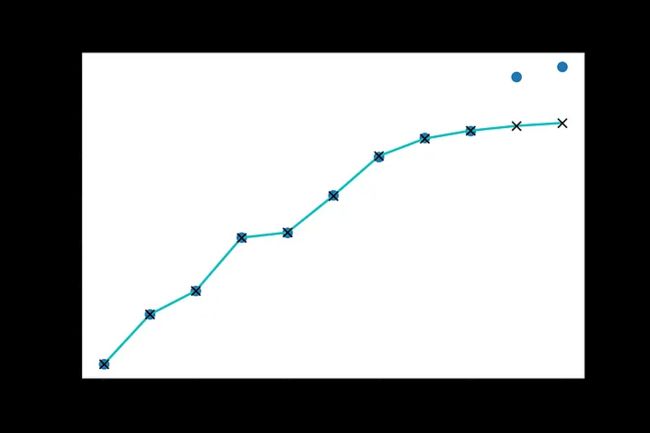
叉点代表我们在训练神经网络5万个epoch后的预测。蓝点代表实际数据点(上场分钟数)。由于故意的噪声导致训练样本变平,模型不能完美地捕捉线性关系。移除模型中的tanh层将移除非线性,迫使模型近似回归输出。
虽然它不是很成功,但这个初始的神经网络是一个概念验证,我们可以开发出序列模型,而不仅仅是将所有的时间步输入在一起。然而,如果没有更多关于过去的信息,并且没有存储和调用这些信息的能力,模型在顺序数据上的性能将非常有限。
LSTM原理
最简单的神经网络假设输入和输出之间的关系与先前的输出状态无关。它假设函数形状可以单独从输入中学习。在连续数据的情况下,这种假设是不正确的。在任何一个特定时间步的函数值可以被认为是直接受过去时间步的函数值的影响。这些值之间存在时间依赖性。长短期记忆网络(LSTM)是一种循环神经网络,在学习这种时间依赖性方面表现出色。
LSTM的关键是单元状态,它允许信息从一个单元流到另一个单元。这代表了LSTM的记忆,可以随着时间的推移更新,更改或忘记。LSTM中进行这种更新的组件称为门,它调节单元所包含的信息。门可以被看作是神经网络层和逐点操作的组合。

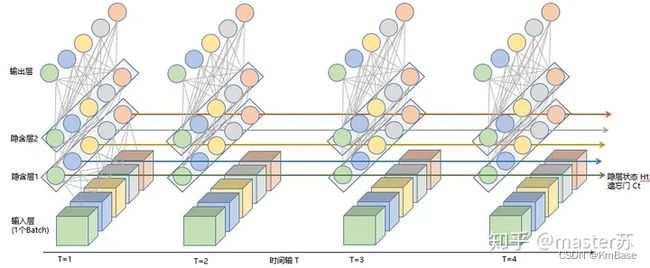
上图是RNN循环神经网络经典的结构图,LSTM只是对隐含层节点A做了改进,整体结构不变。对于上图,中间的A节点隐含层,左边是表示只有一层隐含层的LSTM网络,所谓LSTM循环神经网络就是在时间轴上的循环利用,在时间轴上展开后得到右图。右图中,我们看Xt表示序列,下标t是时间轴,所以,A的数量表示的是时间轴的长度,是同一个神经元在不同时刻的状态(Ht),不是隐含层神经元个数。 我们知道,LSTM网络在训练时会使用上一时刻的信息,加上本次时刻的输入信息来共同训练。
LSTM核心公式
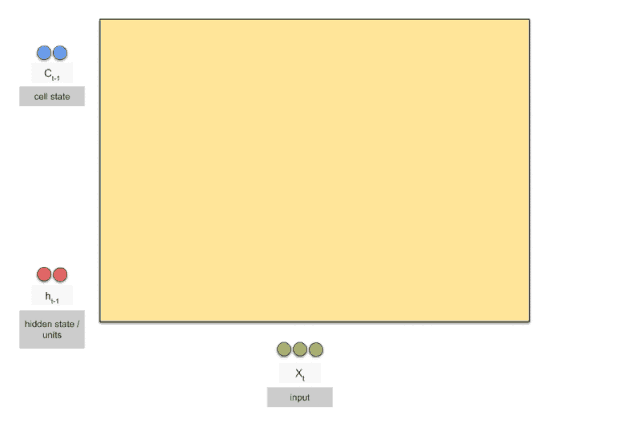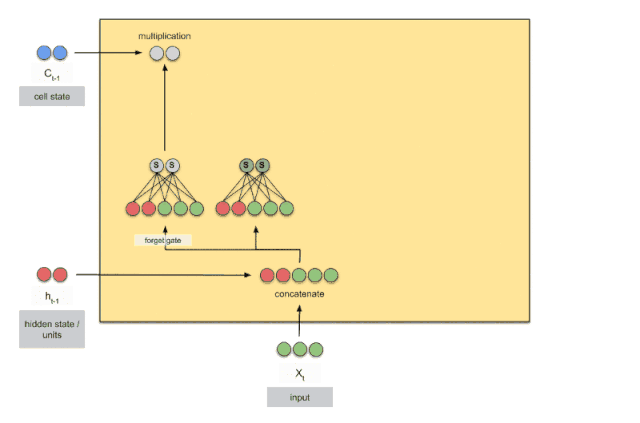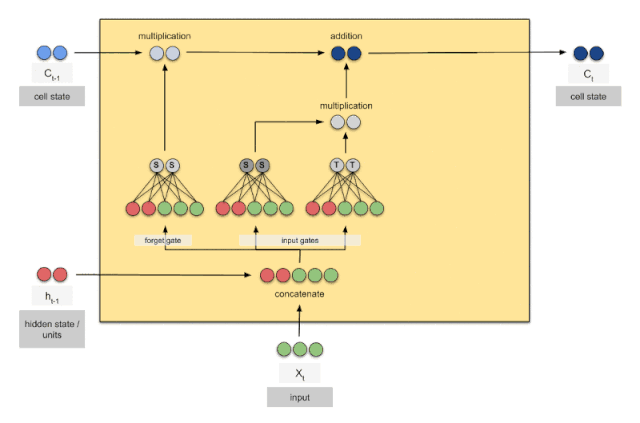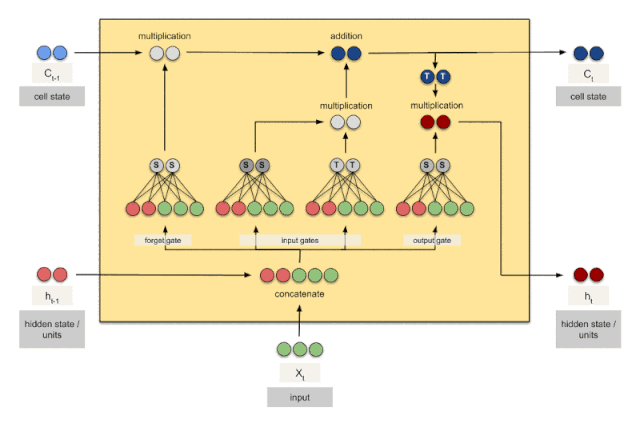
i t = σ ( W i i x t + b i i + W h i h t − 1 + b h i ) (1) i_t = \sigma(W_{ii}x_t+b_{ii}+W_{hi}h_{t-1}+b_{hi})\tag{1} it=σ(Wiixt+bii+Whiht−1+bhi)(1) f t = σ ( W i f x t + b i f + W h f h t − 1 + b h f ) (2) f_t = \sigma(W_{if}x_t+b_{if}+W_{hf}h_{t-1}+b_{hf})\tag{2} ft=σ(Wifxt+bif+Whfht−1+bhf)(2) o t = σ ( W i o x t + b i o + W h o h t − 1 + b h o ) (3) o_t = \sigma(W_{io}x_t+b_{io}+W_{ho}h_{t-1}+b_{ho})\tag{3} ot=σ(Wioxt+bio+Whoht−1+bho)(3) g t = tanh ( W i g x t + b i g + W h g h t − 1 + b h g ) (4) \quad g_t = \tanh(W_{ig}x_t+b_{ig}+W_{hg}h_{t-1}+b_{hg})\tag{4} gt=tanh(Wigxt+big+Whght−1+bhg)(4) c t = f t ⊙ c t − 1 + i t ⊙ g t (5) c_t = f_t\odot c_{t-1}+i_t\odot g_t\qquad\qquad\qquad\tag{5} ct=ft⊙ct−1+it⊙gt(5) h t = o t ⊙ tanh ( c t ) (6) h_t = o_t \odot \tanh(c_t)\qquad\qquad\qquad\qquad \tag{6} ht=ot⊙tanh(ct)(6)

上图是一个时刻的LSTM的内部结构图,多个时刻就是下图在横向上拼接组成。从图中我们可以看到有三个门,即输⼊门(input gate)、遗忘门(forget gate)和输出门(output gate),以及记忆细胞(某些⽂献把记忆细胞当成⼀种特殊的隐藏状态),从⽽记录额外的信息。具体公式说明参考>>从工程角度理解LSTM

可以看到中间的 cell 里面有四个黄色小框,每一个小黄框代表一个前馈网络层,对,就是经典的神经网络的结构,num_units就是这个层的隐藏神经元个数,就这么简单。其中1、2、4的激活函数是 sigmoid,第三个的激活函数是 tanh。
- cell 的状态是一个向量,是有多个值的
- 上一次的状态 h(t-1)是怎么和下一次的输入 x(t)结合(concat)起来的,这也是很多资料没有明白讲的地方,也很简单,concat, 直白的说就是把二者直接拼起来,比如x是28位的向量,h(t-1)是128位的,那么拼起来就是156位的向量,就是这么简单。
- cell 的权重是共享的,这是什么意思呢?这是指这张图片上有三个绿色的大框,代表三个 cell 对吧,但是实际上,它只是代表了一个 cell在不同时序时候的状态,所有的数据只会通过一个 cell,然后不断更新它的权重。
- 那么一层的 LSTM 的参数有多少个?根据第 3点的说明,我们知道参数的数量是由 cell 的数量决定的,这里只有一个 cell,所以参数的数量就是这个 cell 里面用到的参数个数。假设num_units 是128,输入是28位的,那么根据上面的第 2 点,可以得到,四个小黄框的参数一共有128+28)(1284),也就是156 * 512,可以看看 TensorFlow 的最简单的 LSTM的案例,中间层的参数就是这样,不过还要加上输出的时候的激活函数的参数,假设是10个类的话,就是128*10的 W 参数和10个bias.
- cell 最上面的一条线的状态即 s(t) 代表了长时记忆,而下面的 h(t)则代表了工作记忆或短时记忆。
Pytorch LSTM
我们的问题是看看LSTM是否可以“学习”正弦波。这实际上是Pytorch社区中一个相对有名的(读作:臭名昭著)例子。这然而,这个例子是旧的,大多数人发现代码要么不能为他们编译,要么不会收敛到任何合理的输出。(快速的Google搜索给出了一系列关于这个例子的Stack Overflow问题和问题。在这里,我们将分解并一步一步地修改他们的代码。
生成数据
我们开始生成100个不同正弦波的样本,每个正弦波具有相同的频率和振幅,但在x轴上的点略有不同。
N = 100 # number of samples
L = 1000 # length of each sample (number of values for each sine wave)
T = 20 # width of the wave
x = np.empty((N,L), np.float32) # instantiate empty array
x[:] = np.arange(L)) + np.random.randint(-4*T, 4*T, N).reshape(N,1)
y = np.sin(x/1.0/T).astype(np.float32)
让我们看看上面的代码。N是采样数;也就是说,我们生成100个不同的正弦波。许多人在这一点上直觉地绊倒了。由于我们习惯于在单个数据点上训练神经网络,例如上面简单的Klay Thompson示例,因此很容易将N视为我们测量正弦函数的点的数量。这是错误的;我们正在生成N个不同的正弦波,每个正弦波都有许多点。LSTM网络通过检查不是一个正弦波而是许多正弦波来学习。
接下来,我们实例化一个空数组x。将此数组视为沿x轴沿着的点的样本。该阵列具有100行(表示100个不同的正弦波),并且每行是1000个元素长(表示L,或正弦波的粒度,即每个波中不同采样点的数量)。然后,我们通过对前1000个整数点进行采样来填充x,然后在T控制的某个范围内添加一个随机整数,其中x[:]只是沿着沿着行添加整数的语法。请注意,我们必须将第二个随机整数整形为(N, 1),以便Numpy能够将其广播到x的每一行。nbsp;你好 最后,我们简单地将Numpy sine函数应用于x,并让broadcasting将该函数应用于每行中的每个样本,每行创建一个正弦波。我们将其转换为类型float32。我们可以选择任何单个正弦波并使用Matplotlib绘制它。让我们选取索引为0的第一个采样正弦波。
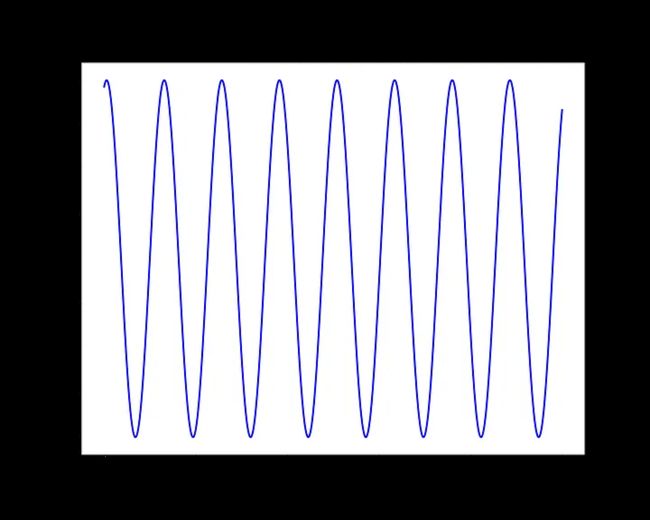
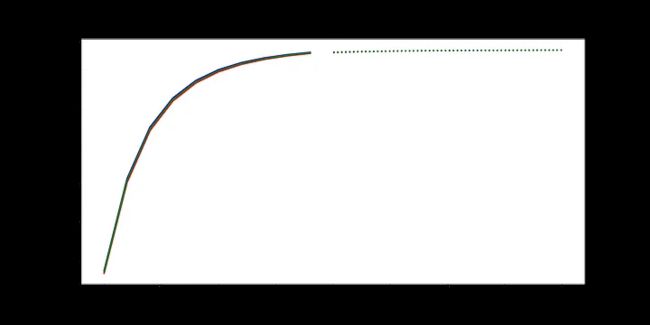
生成的100个正弦波之一,将用于我们的LSTM模型。每个正弦波都有1000个采样点,我们使用正弦函数将这些点转换为波形(图片由作者提供)。
为了构建LSTM模型,我们实际上只有一个nn模块专门为LSTM单元调用。首先,我们将呈现整个模型类(一如既往地继承自nn.Module),然后逐段地遍历它。
class LSTM(nn.Module):
def __init__(self, hidden_layers=64):
super(LSTM, self).__init__()
self.hidden_layers = hidden_layers
# lstm1, lstm2, linear are all layers in the network
self.lstm1 = nn.LSTMCell(1, self.hidden_layers)
self.lstm2 = nn.LSTMCell(self.hidden_layers, self.hidden_layers)
self.linear = nn.Linear(self.hidden_layers, 1)
def forward(self, y, future_preds=0):
outputs, num_samples = [], y.size(0)
h_t = torch.zeros(n_samples, self.hidden_layers, dtype=torch.float32)
c_t = torch.zeros(n_samples, self.hidden_layers, dtype=torch.float32)
h_t2 = torch.zeros(n_samples, self.hidden_layers, dtype=torch.float32)
c_t2 = torch.zeros(n_samples, self.hidden_layers, dtype=torch.float32)
for time_step in y.split(1, dim=1):
# N, 1
h_t, c_t = self.lstm1(input_t, (h_t, c_t)) # initial hidden and cell states
h_t2, c_t2 = self.lstm2(h_t, (h_t2, c_t2)) # new hidden and cell states
output = self.linear(h_t2) # output from the last FC layer
outputs.append(output)
for i in range(future_preds):
# this only generates future predictions if we pass in future_preds>0
# mirrors the code above, using last output/prediction as input
h_t, c_t = self.lstm1(output, (h_t, c_t))
h_t2, c_t2 = self.lstm2(h_t, (h_t2, c_t2))
output = self.linear(h_t2)
outputs.append(output)
# transform list to tensor
outputs = torch.cat(outputs, dim=1)
return outputs
初始化
初始化的关键步骤是声明Pytorch LSTMCell。您可以在这里找到文档。该单元有三个主要参数:
- input_size:输入x中的预期特征数。
- hidden_size:处于隐藏状态的特征数量h。
- bias:默认为true,一般情况下,我们保持这种状态。
你们中的一些人可能知道一个名为torch.nn的单独的LSTM类。这两者之间的区别在这里并不重要,但要知道,当使用函数式API从头定义我们自己的模型时,LSTMCell更加灵活。
请记住,LSTM单元的参数与输入不同。这里的参数在很大程度上控制了预期输入的形状,因此Pytorch可以设置适当的结构。输入是我们输入到单元中的实际训练示例或预测示例。 我们使用两个LSTM单元定义了两个LSTM层。就像卷积神经网络一样,设置输入和隐藏大小的关键在于两层相互连接的方式。对于第一个LSTM单元,我们传入一个大小为1的输入。回想一下为什么会这样:在LSTM中,我们不需要传入一个切片的输入数组。我们不需要在数据上滑动窗口,因为记忆和遗忘门会为我们处理单元状态。我们不需要每次都用旧数据专门手动输入模型,因为模型有能力回忆这些信息。这就是LSTM如此特别的原因。
然后,我们给给予第一个LSTM单元一个隐藏的大小,这个大小由我们声明类n_hidden时的变量控制。这个数字是相当随意的;在这里,我们选择64。如上所述,这将成为我们传递到下一个LSTM单元的各种输出,就像在CNN中一样:最后一步的输出大小将成为下一步的输入大小。在这个单元格中,我们有一个大小为hidden_size的输入,还有一个大小为hidden_size的隐藏层。然后我们将这个大小为hidden_size的输出传递给一个线性层,它本身输出一个大小为1的标量。我们输出一个标量,因为我们只是试图预测该特定时间步的函数值y。
在构建模型的这个阶段,需要记住的最重要的事情之一是输入和输出的大小:我从什么映射到什么?
前向传播方法
在前向方法中,一旦LSTM的各个层都被实例化为正确的大小,我们就可以开始关注通过网络移动的实际输入。一个LSTM单元接受以下输入:input, (h_0, c_0)。
- input:一个形状的输入张量(batch,input_size),我们在创建LSTM单元时声明了input_size。
- h_0:一个张量,包含batch中每个元素的初始隐藏状态,形状为(batch,hidden_size)。
- c_0:一个张量,包含batch中每个元素的初始单元状态,形状为(batch,hidden_size)。
为了连接两个LSTM单元(以及第二个LSTM单元与线性的全连接层),我们还需要知道LSTM单元实际输出的内容:形状为(h_1, c_1)的张量。
- h_0:一个张量,包含batch中每个元素的下一个隐藏状态,形状为(batch,hidden_size)。
- c_0:一个张量,包含batch中每个元素的下一个单元状态,形状为(batch,hidden_size)。
这里,我们的批量大小是100,这是由我们输入的第一个维度给出的;因此,我们取n_samples = x.size(0)。由于我们知道隐藏状态和单元状态的形状都是(batch, hidden_size),因此我们可以实例化一个这种大小的零张量,并为我们的两个LSTM单元这样做。
下一步可以说是最困难的。我们必须输入一个适当形状的张量。在这里,这将是一个m点的张量,其中m是我们对每个序列的训练大小。然而,在Pytorch split()方法中(文档在这里),如果没有传入参数split_size_or_sections,它将简单地将每个张量拆分为大小为1的块。我们希望将此沿着每个单独的批进行拆分,因此我们的维度将是行,这相当于维度1。
当我们以这种方式向量化数组时,检查输出形状总是一个好主意。假设我们为测试集选择了三条正弦曲线,并将其余的用于训练。我们可以在split方法中检查我们的训练输入是什么样子的:
a = torch.from_numpy(y[3:, :-1])
b = a.split(1, dim=1)
b[0].shape
>>> torch.Size([97, 1])
因此,对于每个样本,我们传入一个包含97个输入的数组,其中一个额外的维度表示它来自一个批次。(Pytorch通常是这样操作的。即使我们将单个图像传递给世界上最简单的CNN,Pytorch也需要一批图像,因此我们必须使用unsqueeze()。然后我们输出一个新的隐藏和单元状态。正如我们从上面所知道的,隐藏状态输出被用作下一个LSTM单元的输入。从第二单元输出的隐藏状态然后被传递到线性层。
很好-我们已经完成了基于我们有数据的实际点的模型预测。 但LSTM的全部意义在于根据过去的输出预测曲线的未来形状。所以,在向前传递的下一个阶段,我们要预测下一个未来的时间步长。回想一下,在上一个循环中,我们通过将第二个LSTM输出传递到线性层来计算要附加到输出数组的输出。这个变量仍然在运行-我们可以访问它并再次将其传递给我们的模型。 这是一个好消息,因为我们可以预测未来的下一个时间步,即我们有数据的最后一个时间步。该模型将其对该最终数据点的预测作为输入,并预测下一个数据点。
output = self.linear(h_t2)
....
for i in range(future_preds):
h_t, c_t = self.lstm1(output, (h_t, c_t))
然后我们再次这样做,现在将预测作为模型的输入。总的来说,除了我们已经对1000个实际有数据的点进行的1000次预测之外,我们还对未来进行了多次预测,以产生长度为future_preds的曲线。
我们要做的最后一件事是连接表示输出的标量张量数组,然后返回它们。就是这样!我们已经构建了一个LSTM,它接受一定数量的输入,并且一个接一个地预测未来一定数量的时间步。
训练模型
在Pytorch中定义训练循环在各种常见应用程序中是非常同质的。然而,在我们的例子中,我们不能通过检查损失来直观地理解模型是如何收敛的。是的,低损失是好的,但是有很多次我在实现低损失后去看模型输出,看到了绝对的垃圾预测。这通常是由于绘图代码中的错误,或者更有可能是模型声明中的错误。因此,我们可以应用于模型评估和调试的最有用的工具是绘制每个训练步骤的模型预测,看看它们是否有所改进。
我们的第一步是弄清楚我们的输入和目标的形状。我们知道数据y的形状为(100,1000)。也就是说,100个不同的正弦曲线,每个1000点。接下来,我们想弄清楚我们的列车测试分割是什么。我们将为测试集保存3条曲线,因此沿y的第一维沿着索引,我们可以将最后97条曲线用于训练集。
现在是时候考虑我们的模型输入了。每次一个,我们希望输入最后一个时间步并获得新的时间步预测。为了做到这一点,我们输入每个正弦波的前999个样本,因为输入最后1000个样本将导致预测第1001个时间步长,我们无法验证,因为我们没有数据。同样,对于训练目标,我们使用前97个正弦波,从每个波的第2个样本开始,使用每个波的最后999个样本;这是因为我们需要一个前一个时间步来实际输入到模型中 - 我们不能什么都不输入。因此,目标在第二维中的起始索引(表示每个波中的样本)是1。这给了我们两个形状数组(97,999)。
# y = (100, 1000)
train_input = torch.from_numpy(y[3:, :-1]) # (97, 999)
train_target = torch.from_numpy(y[3:, 1:]) # (97, 999)
测试输入和测试目标遵循非常类似的推理,除了这次,我们仅索引沿第一维的前三个正弦波沿着。正如我们所期望的那样,其他一切都是完全相同的:除了批量输入大小(97 vs 3)之外,我们需要为训练集和测试集提供相同的输入和输出。
test_input = torch.from_numpy(y[:3, :-1]) # (3, 999)
test_target = torch.from_numpy(y[:3, 1:]) # (3, 999)
我们现在需要实例化训练循环的主要组件:模型本身、损失函数和优化器。该模型只是我们LSTM类的一个实例,我们将用于回归问题的损失函数是nn.MSELoss()。唯一不同的是我们的乐观主义者。代替Adam,我们将使用所谓的有限内存BFGS算法,它本质上归结为估计Hessian矩阵的逆矩阵作为变量空间的指导。你不需要担心细节,但你需要担心optim.LBFGS和其他优化器之间的区别。我们将在下面的训练循环中介绍这一点。
model = LSTM()
criterion = nn.MSELoss()
optimiser = optim.LBFGS(model.parameters(), lr=0.08)
你可能想知道为什么我们要从像Adam这样的标准优化器转换到这个相对未知的算法。LBFGS求解器是一种拟牛顿方法,它使用Hessian的逆来估计参数空间的曲率。在序列问题中,参数空间的特征是大量的长而平坦的山谷,这意味着LBFGS算法通常优于其他方法,如Adam,特别是当没有大量数据时。
最后,我们开始构建训练循环。公平的警告,尽管我试图让它看起来像一个典型的Pytorch训练循环,但会有一些差异。这些主要是我们必须传递给优化器的函数closure,它代表了网络中典型的向前和向后传递。我们通过传入这个函数来用optimiser.step()更新权重。根据Pytorch的说法,函数闭包是一个重新评估模型(向前传递)并返回损失的可调用函数。所以这就是我们要做的。
def training_loop(n_epochs, model, optimiser, loss_fn,
train_input, train_target, test_input, test_target):
for i in range(n_epochs):
def closure():
optimiser.zero_grad()
out = model(train_input)
loss = loss_fn(out, train_target)
loss.backward()
return loss
optimiser.step(closure)
with torch.no_grad():
future = 1000
pred = model(test_input, future=future)
# use all pred samples, but only go to 999
loss = loss_fn(pred[:, :-future], test_target)
y = pred.detach().numpy()
# draw figures
plt.figure(figsize=(12,6))
plt.title(f"Step {i+1}")
plt.xlabel("x")
plt.ylabel("y")
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
n = train_input.shape[1] # 999
def draw(yi, colour):
plt.plot(np.arange(n), yi[:n], colour, linewidth=2.0)
plt.plot(np.arange(n, n+future), yi[n:], colour+":", linewidth=2.0)
draw(y[0], 'r')
draw(y[1], 'b')
draw(y[2], 'g')
plt.savefig("predict%d.png"%i, dpi=200)
plt.close()
# print the loss
out = model(train_input)
loss_print = loss_fn(out, train_target)
print("Step: {}, Loss: {}".format(i, loss_print))
训练循环的开始和其他普通训练循环一样。但是,请注意,向前和向后传递的典型步骤在函数closure中捕获。这只是在Pytorch中设计优化器函数的一个特性。我们在闭包中返回损失,然后在optimiser.step()期间将此函数传递给优化器。这就是训练步骤。
接下来,我们要绘制一些预测,这样我们就可以在执行过程中对结果进行合理性检查。为此,我们需要获取测试输入,并将其传递给模型。这就是我们在模型本身中包含的未来参数将派上用场的地方。回想一下,通过模型向前传递一些非负整数future将在实际样本的最后一次输出之后给予我们未来的预测。这使我们能够看到模型是否推广到未来的时间步长。然后,我们将此输出从当前计算图中分离出来,并将其存储为numpy数组。
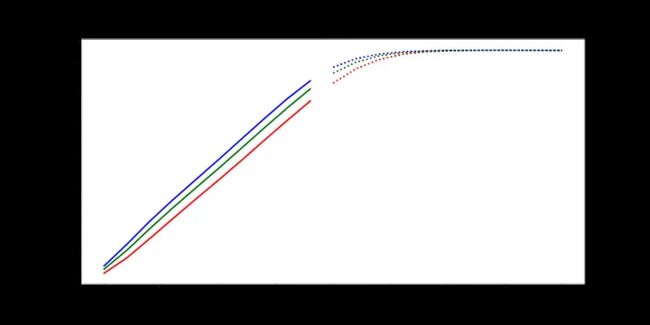
最后,我们编写一些简单的代码来绘制模型在每个时期对测试集的预测。只有三条测试正弦曲线,所以我们只需要调用draw函数三次(我们将用不同的颜色绘制每条曲线)。绘制的线表示未来的预测,实线表示当前数据范围内的预测。
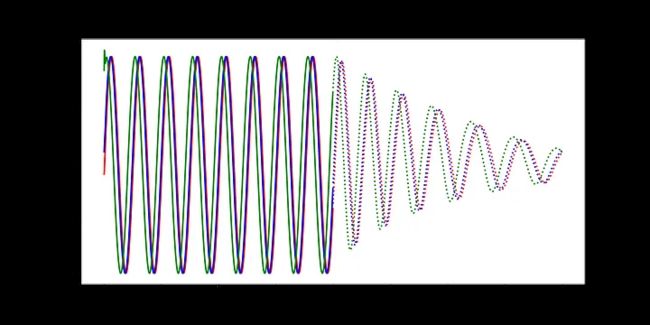

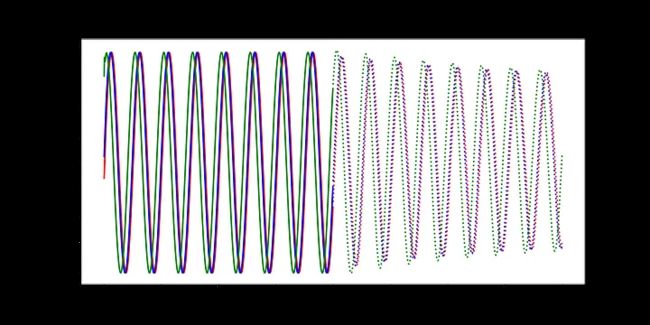
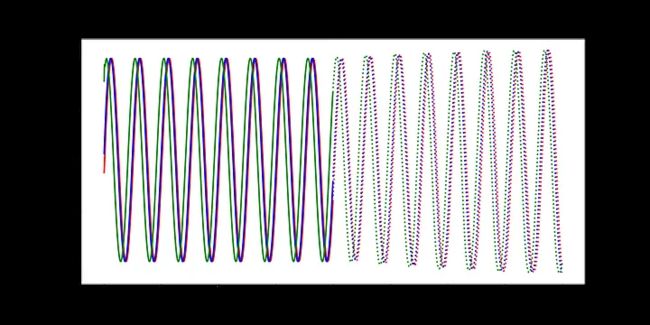
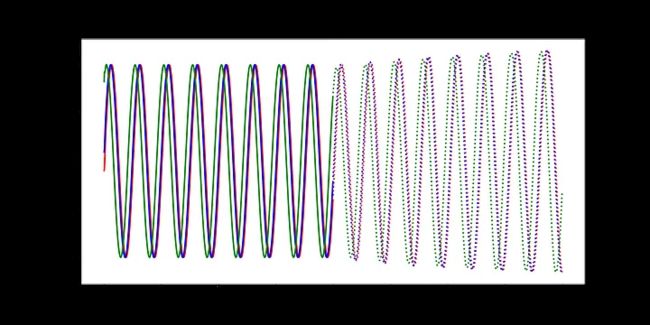
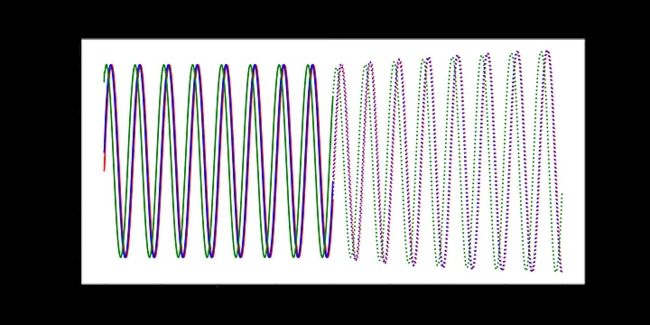
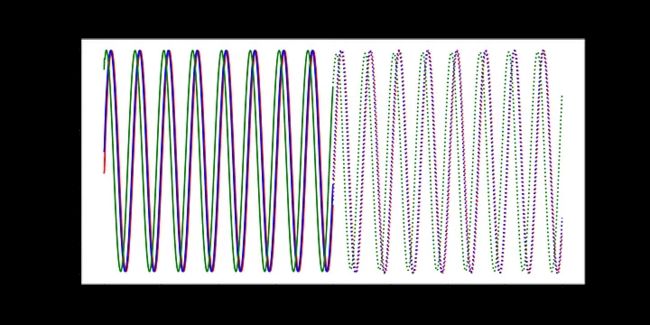
随着时间的推移,预测显然会有所改善,损失也会下降。我们的模型工作正常:到第8个epoch,模型已经学习了正弦波。然而,如果你继续训练模型,你可能会看到预测开始做一些有趣的事情。这是因为,在每个时间步,LSTM依赖于前一个时间步的输出。如果第1001个预测的预测稍微改变,这将干扰预测一直到预测2000,导致无意义的曲线。有很多方法可以解决这个问题,但它们超出了本文的范围。现在最好的策略是观察图,看看这种误差积累是否开始发生。然后,你可以回到一个更早的时代,或者训练过去,看看会发生什么。
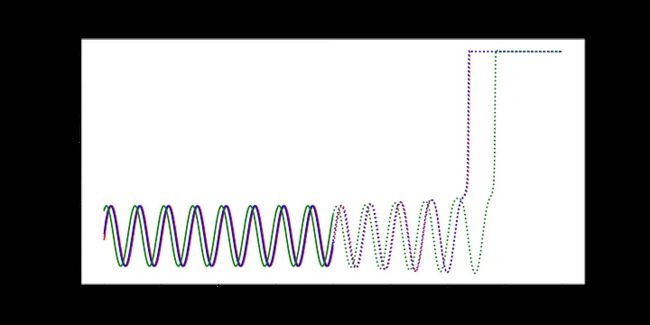
如果你在让LSTM收敛方面遇到困难,这里有一些你可以尝试的事情:
- 通过更改隐藏层的大小来减少模型参数的数量(甚至可能减少到15个)。这减少了模型搜索空间。
- 尝试通过减少传递到第二个单元格的hidden_size来从第一个LSTM单元格到第二个单元格进行下采样。您也可以从第二个LSTM单元到线性全连接层进行此操作。
- 添加batchnorm正则化,通过对较大的权重值进行惩罚来限制权重的大小,从而使损失更平滑。
- 添加dropout,它在每个时期将整个模型中神经元输出的随机部分归零。这每次都会生成略有不同的模型,这意味着模型被迫更少地依赖于单个神经元。
如果你实现了最后两个策略,记得在训练过程中调用model.train()来实例化正则化,并在预测和评估过程中使用model.eval()关闭正则化。
自动化模型构建
如果我们仍然不能将LSTM应用于其他形状的输入,那么整个练习就毫无意义。让我们生成一些新的数据,除了这一次,我们将随机生成曲线的数量和每条曲线中的样本。我们不知道这些参数的实际值是什么,所以这是一个完美的方法来看看我们是否可以基于输入和输出形状之间的关系来构建LSTM。
N = np.random.randint(50, 200) # number of samples
L = np.random.randint(800, 1200) # length of each sample (number of values for each sine wave)
T = np.random.randint(10, 30) # width of the wave
x = np.empty((N,L), np.float32) # instantiate empty array
x[:] = np.arange(L) + np.random.randint(-4*T, 4*T, N).reshape(N,1)
y = np.cos(np.sin(x/1.0/T)**2).astype(np.float32)
然后,我们可以通过确定我们想要用于训练集的每条曲线中的样本百分比来更改以下输入和输出形状。
train_prop = 0.95
train_samples = round(N * train_prop)
test_samples = N - train_samples
因此,输入和输出形状变为:
# y = (N, L)
train_input = torch.from_numpy(y[test_samples:, :-1]) # (train_samples, L-1)
train_target = torch.from_numpy(y[test_samples:, 1:]) # (train_samples, L-1)
test_input = torch.from_numpy(y[:test_samples, :-1]) # (train_samples, L-1)
test_target = torch.from_numpy(y[:test_samples, 1:]) # (train_samples, L-1)
你可以通过在LSTM中运行这些输入和目标来验证这是否有效(提示:确保根据输入的长度为future_preds实例化一个变量)。
让我们看看是否可以将其应用于最初的Klay Thompson示例。如果我们要将它提供给我们的LSTM,我们需要生成多个分钟集。也就是说,我们将生成100个不同的假设分钟,克莱·汤普森在100个不同的假设世界中演奏。我们将把其中的95个输入训练,并绘制剩下的5个中的3个,看看我们的模型是如何学习的。
N = 100 # number of theoretical series of games
L = 11 # number of games in each series
x = np.empty((N,L), np.float32) # instantiate empty array
x[:] = np.arange(L))
y = (1.6*x + 4).astype(np.float32)
# add some noise
for i in range(len(y)):
y[i] += np.random.normal(10, 1)
在使用上面的代码根据L和N重塑输入和输出之后,我们运行模型并实现以下内容:
training_loop(n_epochs = 10,
model = model,
optimiser = optimiser,
loss_fn = criterion,
L = L,
train_input = train_input,
train_target = train_target,
test_input = test_input,
test_target = test_target)
Step: 0, Loss: 7.279130458831787
Step: 1, Loss: 1.4280033111572266
Step: 2, Loss: 0.5719900727272034
Step: 3, Loss: 0.31642651557922363
Step: 4, Loss: 0.20579740405082703
Step: 5, Loss: 0.15880005061626434
Step: 6, Loss: 0.1370033472776413
Step: 7, Loss: 0.11637765169143677
Step: 8, Loss: 0.09049651771783829
Step: 9, Loss: 0.06212589889764786
非常有趣!最初,LSTM也认为曲线是对数的。虽然它在经过一点训练后发现前11场比赛的曲线是线性的,但它坚持为未来的比赛提供对数曲线。最吸引人的是,LSTM是正确的–Klay不能线性增加他的比赛时间,因为一场篮球比赛只有48分钟,而且大多数这样的过程都是对数的。 显然,LSTM不可能知道这一点,但无论如何,看看模型最终如何解释我们的玩具数据是很有趣的。未来的任务可能是尝试LSTM的超参数,看看是否有可能让它学习未来时间步长的线性函数。此外,我喜欢创建一个Python类来将所有这些函数存储在一个位置。然后,你可以用数据创建一个对象,你可以编写函数来读取数据的形状,并将其提供给适当的LSTM构造器。
总结
总之,在Pytorch中为单变量时间序列数据创建LSTM不需要过于复杂。然而,在线可用资源的缺乏(特别是不关注自然语言形式的顺序数据的资源)使得学习如何构建这种循环模型变得困难。希望这篇文章能为您提供设置输入和目标的指导,为LSTM forward方法编写Pytorch类,使用我们新的优化器的怪癖定义训练循环,以及使用可视化工具(如绘图)进行调试。
如果你想了解更多关于LSTM单元背后的数学知识,我强烈推荐这篇文章,它漂亮地列出了LSTM的基本方程(我与作者没有联系)。我还建议尝试将上面的代码修改为多变量时间序列。所有的核心思想都是一样的–你只需要考虑如何扩展输入的维度。
参考文献
https://zhuanlan.zhihu.com/p/139617364
https://towardsdatascience.com/pytorch-lstms-for-time-series-data-cd16190929d7