Go 实现选择排序算法及优化

选择排序

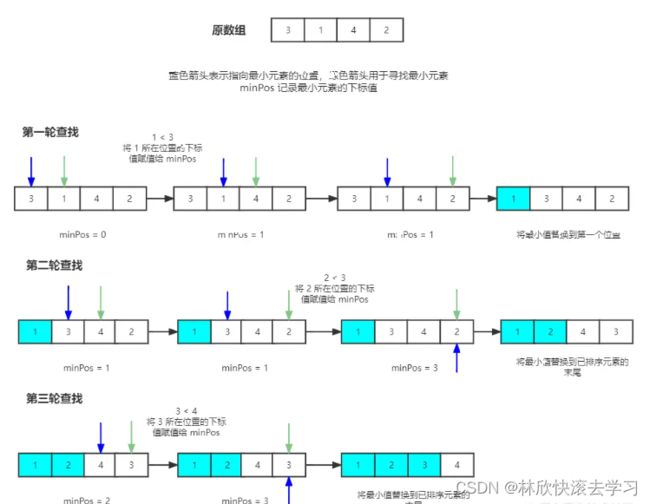
选择排序是一种简单的比较排序算法，它的算法思路是首先从数组中寻找最小（大）的元素，然后放到数组中的第一位，接下来继续从未排序的元素中寻找最小（大）元素，然后放到已排序元素的末尾，依次类推，直到所有元素被排序。

图片演示

普通算法

import "fmt"

func main() {
    nums := [8]int{8, 2, 3, 1, 6, 5, 7, 4}
    fmt.Println("原数组：", nums)
    fmt.Println("--------------------------------")
    SelectionSort(nums)
}

func SelectionSort(nums [8]int) {
    for i := 0; i < len(nums)-1; i++ {
        minPos := i
        for j := i + 1; j < len(nums); j++ {
            if nums[minPos] > nums[j] {
                    minPos = j
            }
        }
        nums[i], nums[minPos] = nums[minPos], nums[i]
        fmt.Printf("第 %d 轮后：%v\n", i+1, nums)
    }
    fmt.Println("--------------------------------")
    fmt.Println("排序后的数组：", nums)
}

执行结果：

原数组： [8 2 3 1 6 5 7 4]
--------------------------------
第 1 轮后：[1 2 3 8 6 5 7 4]
第 2 轮后：[1 2 3 8 6 5 7 4]
第 3 轮后：[1 2 3 8 6 5 7 4]
第 4 轮后：[1 2 3 4 6 5 7 8]
第 5 轮后：[1 2 3 4 5 6 7 8]
第 6 轮后：[1 2 3 4 5 6 7 8]
第 7 轮后：[1 2 3 4 5 6 7 8]
--------------------------------
排序后的数组： [1 2 3 4 5 6 7 8]

升序排序。
使用 i 变量表示最小元素的待放位置。
minPos 变量记录最小元素的的下标值，默认为 i。
通过变量 j 去寻找最小元素，j 从 i + 1 的位置开始寻找。
找到比 nums[minPos] 还小的元素，则将 j 的下标值赋给 minPos。
一轮下来，将最小元素的位置 minPos 与 i 的位置互换，然后继续下一轮寻找，直到所有元素都被排序。
该算法的时间复杂度为 O(N²)。

优化算法

普通算法是寻找最小值或最大值，然后放到指定位置。优化算法的改进点是同时寻找最小值和最大值。

import (
    "fmt"
)

func main() {
    nums := [4]int{3, 1, 4, 2}
    fmt.Println("原数组：", nums)
    fmt.Println("--------------------------------")
    SelectionSort(nums)
}

func SelectionSort(nums [4]int) {
    for left, right := 0, len(nums)-1; left <= right; {
        minPos := left
        maxPos := left
        for i := left + 1; i <= right; i++ {
            if nums[minPos] > nums[i] {
                minPos = i
            }
            if nums[maxPos] < nums[i] {
                maxPos = i
            }
        }
        nums[left], nums[minPos] = nums[minPos], nums[left]
        // 如果最大值刚好是在 left，待放最小值的位置，那么最大值就会被换走，所以需要判断一下
        if maxPos == left {
            maxPos = minPos
        }
        nums[right], nums[maxPos] = nums[maxPos], nums[right]
        fmt.Printf("第 %d 轮后：%v\n", left+1, nums)
        left++
        right--
    }
    fmt.Println("--------------------------------")
    fmt.Println("排序后的数组：", nums)
}

执行结果：

原数组： [8 2 3 1 6 5 7 4]
--------------------------------
第 1 轮后：[1 2 3 4 6 5 7 8]
第 2 轮后：[1 2 3 4 6 5 7 8]
第 3 轮后：[1 2 3 4 5 6 7 8]
第 4 轮后：[1 2 3 4 5 6 7 8]
--------------------------------
排序后的数组： [1 2 3 4 5 6 7 8]

left 变量表示待放最小值的位置，right 变量表示待放最大值的位置。minPos 记录最小值的下标值，maxPos 记录最大值的下标值，通过变量 i 去寻找最小值和最大值，寻找完毕后将它们进行交换。
有一个注意的地方是，如果最大值刚好是在 left ，待放最小值的位置，那么最大值就会被换到 minPos 的位置，所以需要判断一下，纠正下标值。
从执行结果来看，优化后的算法效率快了一倍，但是时间复杂度仍为 O(N²)。

小结

本文简单介绍了什么是选择排序，然后通过图片的方式演示选择排序的过程，接下来是实现 O(N²) 时间复杂度的算法，最后优化算法，从结果来看，优化后的算法效率快了一倍，但是时间复杂度仍为 O(N²)。