线性表操作的实现--单链表（链式存储结构）

本文参考朱战力老师的数据结构与算法--使用C语言一书

目录

文章目录

前言

一、链表是什么？

二、具体实现

1.单链表的定义

2.初始化ListInitiate（SLNode **head）

3.求当前元素的个数ListLength（SLNode *head）

4.插入ListInsert（SLNode *head，int i，DataType x）

5.删除ListDelete（SLNode *head，int i，DataType *x）

6.取元素ListGet（SLNode *head，int i，DataType *x）

 7.撤销单链表Destroy（SLNode **head）

  8.链表排序ListSort(SLNode* head)

  9.链表查找ListSearch(SLNode* head, DataType target)

  10.小试牛刀

总结

---

前言

        本文所介绍的内容为数据结构与算法的基础内容--顺序表操作的实现，笔者通过不断的深入学习发现，后续的数据结构中，包括堆栈、队列、串、数组、表、数和二叉树无不是通过线性表去实现，故很好的理解线性表的操作对于广大的读者来说非常的有必要！

---

一、链表是什么？

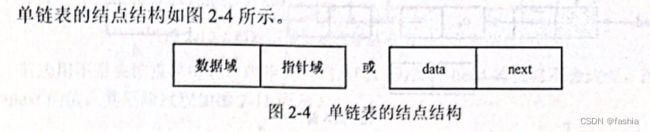
        本篇文章讨论线性表的链式存储结构和链式存储结构下操作的实现。链式存储结构存储线性表元素的方法是，把存储有元素的结点用指针域构造成链。指针是指向物理内存单元地址的变量。我们把一个由元素域及一个或若干个指针域组成的结构体称为一个结点。其中，数据域用来存放元素，指针域用来构造元素之间的关联关系。链式存储结构的特点是，元素间的逻辑关系表现在结点的链接关系上。链式存储结构的线性表称为链表。根据指针域的不同和结点构造链的方法不同，链表主要有单链表、循环单链表和双向循环链表三种。其中单链表是最经常使用的链表。

二、具体实现

1.单链表的定义

代码如下（示例）：

typedef struct Node {
    DataType data;
    struct Node* next;
}SLNode;

2.初始化ListInitiate（SLNode **head）

代码如下（示例）：

void ListInitiate(SLNode** head) {	//初始化
	*head = (SLNode*)malloc(sizeof(SLNode));	//申请头结点，由head指示其地址
	(*head)->next = NULL;	//置结束标志NULL
}

说明：在初始化操作前，头指针参数head没有具体的地址值。在初始化操作时，头指针参数head才得到了具体的地址值，而这个地址值要返回给调用函数，所以，此时头指针参数head要设计成双重指针（指针的指针）类型。如果此时头指针参数head设计成指针类型，那么调用函数将无法得到在初始化函数中被赋值的头指针参数head的值。

3.求当前元素的个数ListLength（SLNode *head）

代码如下（示例）：

int ListLength(SLNode* head) {
	SLNode* p = head;	//p指向头结点
	int size = 0;	//size初始为0

	while (p->next != NULL) {	//循环计数
		p = p->next;
		size++;
	}
	return size;
}

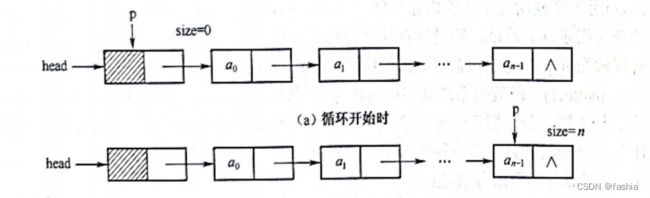
算法实现过程：

4.插入ListInsert（SLNode *head，int i，DataType x）

代码如下（示例）：

int ListInsert(SLNode* head, int i, DataType x) {
	//在带头结点的单链表head的第i给结点前插入一个存放元素x的结点
	//插入成功则返回1，失败则返回0
	SLNode* p, * q;
	int j;
	p = head;
	j = -1;
	while (p->next != NULL && j < i - 1) {
		//最终让指针p指向第i-1个结点
		p = p->next;
		j++;
	}

	if (j != i - 1) {
		printf("插入元素位置参数错！");
		return 0;
	}

	q = (SLNode*)malloc(sizeof(SLNode));	//生成新结点
	q->data = x;							//新结点数据域赋值

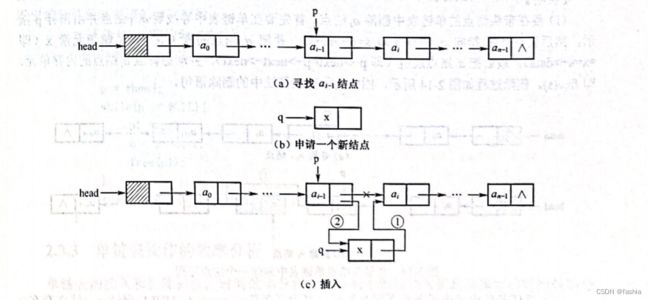
	q->next = p->next;						//插入步骤1
	p->next = q;							//插入步骤2
	return 1;
}

算法实现过程：

5.删除ListDelete（SLNode *head，int i，DataType *x）

代码如下（示例）：

int ListDelete(SLNode* head, int i, DataType* x) {
	//删除带头结点单链表head的第i（0~size-1)个结点
	//被删除结点的数据域值由x带回，删除成功则返回1，失败则返回0
	SLNode* p, * s;
	int j;
	p = head;
	j = -1;

	while (p->next != NULL && p->next->next != NULL && j < i - 1) {
		//循环结束时指针p指向第i-1个结点
		p = p->next;
		j++;
	}

	if (j != i - 1) {
		printf("删除元素位置参数错！");
		return 0;
	}

	s = p->next;		//指针s指向第i个结点
	*x = s->data;		//把指针s所指结点的数据域值赋予x
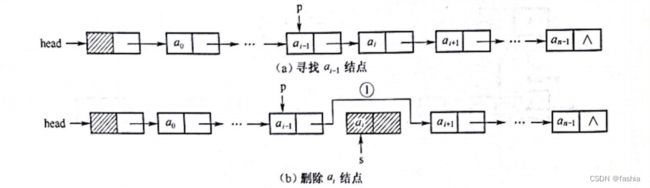
	p->next = p->next->next;		//删除
	free(s);			//释放指针s所指结点的内存空间
	return 1;
}

算法实现过程：

6.取元素ListGet（SLNode *head，int i，DataType *x）

代码如下（示例）：

int ListGet(SLNode* head, int i, DataType* x) {
	SLNode* p;
	int j;

	p = head;
	j = -1;
	while (p->next != NULL && j < i) {
		p = p->next;
		j++;
	}

	if (j != i) {
		printf("取元素位置参数错！");
		return 0;
	}

	*x = p->data;
	return 1;
}

 7.撤销单链表Destroy（SLNode **head）

代码如下（示例）：

void Destroy(SLNode** head) {
	SLNode* p, * p1;

	p = *head;
	while (p != NULL) {
		p1 = p;
		p = p->next;
		free(p1);
	}
	*head = NULL;
}

  8.链表排序ListSort(SLNode* head)

代码如下（示例）：

void ListSort(SLNode* head) {
	if (head == NULL || head->next == NULL) {
		return;		//空链表或只有一个结点，无需进行排序
	}

	SLNode* p, * q;
	DataType temp;
	int len = ListLength(head);

	for (int i = 0; i < len - 1; i++)
	{
		p = head->next;
		q = head->next->next;

		for (int j = 0; j < len - 1 - i; j++)
		{
			if (p->data > q->data)
			{
				temp = p->data;
				p->data = q->data;
				q->data = temp;
			}
			p = p->next;
			q = q->next;
		}
	}
}

  9.链表查找ListSearch(SLNode* head, DataType target)

代码如下（示例）：

int ListSearch(SLNode* head, DataType target) {
	if (head == NULL)
	{
		return -1;	//空链表，查找失败
	}

	SLNode* p = head->next;
	int index = 0;

	while (p != NULL)
	{
		if (p->data == target)
		{
			return index;	//找到目标值，返回索引
		}
		p = p->next;
		index++;
	}
	return -1;
}

  10.小试牛刀

代码如下（示例）：

#define _CRT_SECURE_NO_WARNINGS
#include	//包含printf（）
#include	//包含malloc（）等函数
typedef int DataType;	//定义DataType为int
#include"LinList.h"	//包含LinList.h头文件
void main() {
	SLNode* head;	//定义头指针变量
	int i, x;

	ListInitiate(&head);	//初始化
	for (i = 0; i < 10; i++)	//插入10个元素
	{
		ListInsert(head, i, i + 1);
	}
	ListDelete(head, 3, &x);	//删除元素4
	for (i = 0; i < ListLength(head); i++) {	//显示当前的元素
		ListGet(head, i, &x);	//取元素
		printf("%d	", x);		//显示
	}

	// 测试排序函数
	printf("\n\n排序后的链表：\n");
	ListSort(head);
	for (i = 0; i < ListLength(head); i++) {	//显示当前的元素
		ListGet(head, i, &x);	//取元素
		printf("%d	", x);		//显示
	}

	// 测试查找函数
	int target = 7;
	int index = ListSearch(head, target);
	if (index != -1) {
		printf("\n\n目标值 %d 在链表中的索引位置为 %d\n", target, index);
	}
	else {
		printf("\n\n目标值 %d 不在链表中\n", target);
	}

	Destroy(&head);				//撤销单链表
}

运行结果：

---

总结

        

        单链表是一种常见的数据结构，它由节点组成，每个节点包含数据和指向下一个节点的指针。在本文中，我们实现了单链表的一些基本操作，包括插入、删除、排序和查找等。

        通过插入操作，我们可以在链表中添加新的节点。删除操作可以帮助我们删除指定节点。排序操作可以根据特定的规则对链表进行排序，使得节点按照一定的顺序排列。查找操作可以在链表中寻找特定的节点，并返回其位置或者相关信息。

        这些操作的实现需要注意指针的运用，以确保链表的结构正确。在排序和查找过程中，需要考虑不同的算法和复杂度，选择合适的方法来提高效率。

        总的来说，通过实现这些操作，我们可以灵活地对单链表进行操作，实现了对节点的添加、删除、排序和查找等功能。熟练掌握这些操作为我们日后学习哈希表和二叉树，都打下了非常坚实的基础。