【C数据结构】单链表的实现以及链表和顺序表的优缺点

 

一、链表和顺序表的相辅相成

  在这之前，我们通过顺序表对数据结构开了个头，并且了解到了顺序表是个什么样的情况。

现在让我们来看看顺序表的几个明显缺点：

• 空间不够了就需要扩容，麻烦。
• 由于顺序表储存是一个连续的物理空间，空间不够了以后需要增容，而为了避免频繁增容，一次一般是按倍数去扩充，这就可能存在一定的空间浪费。
• 头部中部插入删除这些操作时间效率低O(N)。

而在链表中，链表可以按需申请空间，不用了就释放空间（更合理的使用了空间），并且头部中部插入删除数据，不需要挪动数据。
 
 

二、认识链表的最简单结构（单链表）

1.单链表的结构：

 【物理结构】
这是在内存中实实在在如何存储的。
  首先假设有一个pList的指针变量储存内存Ox12FFA0，这个内存将会让pList指向第一个链表的结点，这个结点储存了一个有效值（如图中的1），和一个能访问下一个结点的地址（如图中Ox0012FFB0），使得通过这个结点能访问下一个结点，依次构成一个链表。

 
  [逻辑结构]

通过内存访问我们可以表现出箭头指向，这样方便理解，但这是想象出来的，实际并没有箭头。

 

---

 

2.单链表的简单操作实现：

理解完了代码思路，建议自己独立通过思路实现，发现问题，解决问题。
以下分了几个小点，建议理解完一个，自己独立完成一个。
了解一级与二级指针可以看看这里从链表中看到的常见问题

(1)、提前准备（头文件和测试源文件）

首先创建一个头文件SList.h
并且将要实现以下链表的操作

#include
#include
#include

typedef int DateType;

typedef struct SListNode
{
	DateType data;
	struct SListNode* next;
}SLNode;

//打印链表
void SListPrint(SLNode* phead);

//创建一个结点
SLNode* SListCreateNode(DateType x);

//链表尾插
void SListPushBack(SLNode** pphead,DateType x);

//链表头插
void SListPushFront(SLNode** pphead,DateType x);

//链表尾删
void SListPopBack(SLNode** pphead);

//链表头删
void SListPopFront(SLNode** pphead);

//链表指定结点前插入
void SListInsert(SLNode** pphead, SLNode* pos, DateType x);

//链表指定结点删除
void SListErase(SLNode** pphead,SLNode* pos);

//销毁链表
void SListDestroy(SLNode** pphead);

//寻找链表中的结点
SLNode* SListFind(SLNode* phead,DateType x);

//在指定结点后插入
void SListInsertAfter(SLNode* pos, DateType x);

 

创建一个测试文件Test.c，在这里通过调用函数进行测试。
以下将是我们需要看到的效果测试

#include"SList.h"
void Test1() {
	SLNode *sl= NULL;
	int i=1;
	/*SListPushFront(sl, 1);*///测试报错断言
	/*SListPushBack(sl, 1);*///测试报错断言
	SListPushBack(&sl, 1);
	SListPushBack(&sl, 2);
	SListPushBack(&sl, 3);
	SListPushBack(&sl, 4);
	SListPushBack(&sl, 5);
	SListPushBack(&sl, 3);

	/*SListPopBack(&sl);*/
	//SListPopBack(&sl);
	//SListPopBack(&sl);
	//SListPopBack(&sl);
	//SListPopBack(&sl);
	//SListPopBack(&sl);
	//SListPopBack(&sl);


	/*SListPushFront(&sl, 1);*/
	/*SListPushFront(&sl, 2);*/
	//SListPushFront(&sl, 3);
	//SListPushFront(&sl, 4);
	//SListPushFront(&sl, 5);

	/*SListPopFront(&sl);*/

	SListPrint(sl);

	//查找指定元素
	SLNode*pos=SListFind(sl, 2);
	while(pos) 
	{
		printf("第%d个%d,在%p位置\n", i++,pos->data, pos);
		pos = SListFind(pos->next, 2);
	}

	//插入指定元素到指定结点前
	pos = SListFind(sl, 1);
	while (pos)
	{
		SListInsert(&sl, pos, 10);
		pos = SListFind(pos->next, 1);
	}
	SListPrint(sl);

	//插入指定元素到指定结点后O(1)
	pos = SListFind(sl, 3);
	while (pos) 
	{
		SListInsertAfter(pos, 20);
		pos = SListFind(pos->next, 3);
	}
	SListPrint(sl);
	//删除指定元素
	pos = SListFind(sl, 1);
	while (pos) 
	{
		SListErase(&sl, pos);
		pos = SListFind(sl, 1);
	}
	SListPrint(sl);
	SListDestroy(&sl);

}
int main() {

	Test1();//操作的测试
	return 0;

}

 

---

 

(2)、单链表的头插、尾插与创建一个新结点

接下来的操作实现我们放在一个源文件SList.c中
注意要包含头文件

//SList.c
#include"SList.h"

创建一个新结点

//SList.c
//创建新结点
SLNode* SListCreateNode(DateType x)
{
	SLNode* newnode = (SLNode*)malloc(sizeof(SLNode));
	if (newnode == NULL)
	{
		printf("malloc fail");
		exit(-1);
	}
	newnode->data = x;
	newnode->next = NULL;
	return newnode;
}

实现尾插

//SList.c
void SListPushBack(SLNode** pphead, DateType x)
{
	assert(pphead);

	SLNode* newnode = SListCreateNode(x);

	if ((*pphead) == NULL)
	{
		(*pphead) = newnode;
	}
	else
	{
		SLNode* cur = *pphead;
		while (cur->next != NULL)
		{
			cur = cur->next;
		}
		cur->next = newnode;
	}

}

实现头插

//链表头部插入结点
void SListPushFront(SLNode** pphead, DateType x)
{
	assert(pphead);

	SLNode* newnode = SListCreateNode(x);

	newnode->next = (*pphead);
	*pphead = newnode;
}

 

---

 

(3)、单链表的头删、尾删与打印链表

为了防止在代码多的时候遇到报错不好处理，我们写了一点最好先测试一下。

单链表的打印

//SList.c
//链表的打印,在测试页中调用这个函数试试之前的函数调用有没有问题
void SListPrint(SLNode* phead)
{
	while (phead)
	{
		printf("%d ", phead->data);
		phead = phead->next;
	}

	printf("\n");
}

单链表的尾删

//SList.c
//链表删尾结点
void SListPopBack(SLNode** pphead)
{
	assert(pphead && *pphead);

	SLNode* end = *pphead;
	if (end->next == NULL)
	{
		free(end);
		*pphead = NULL;
	}
	else
	{
		while (end->next->next != NULL)
		{
			end = end->next;
		}
		free(end->next);
		end->next = NULL;
	}

}

由于指针直接指向第一个结点，在处理只有一个结点和处理有两个或两个以上的删除情况不同，所以要分开讨论。

单链表的头删

//SList.c
//链表头部删除结点
void SListPopFront(SLNode** pphead) 
{
	assert(pphead && *pphead);

	SLNode* next = *pphead;
	*pphead = next->next;
	free(next);
	next = NULL;
}

 

(4)、单链表的销毁

//SList.c
//链表的销毁
void SListDestroy(SLNode** pphead)
{
	assert(pphead);

	SLNode* p = *pphead;
	SLNode* cur = *pphead;
	while (p)
	{
		p = p->next;
		free(cur);
		cur = p;
	}

	*pphead = NULL;
}

 

---

 

3.单链表的复杂操作实现：

这里包括单链表的查找，指定位置插入以及指定位置删除。

(1)、单链表查找指定数据并返回结点

//SList.c
//链表查找指定数据返回结点
SLNode* SListFind(SLNode* phead, DateType x)
{

	while (phead)
	{
		if (phead->data == x)
		{
			return phead;
		}
		phead = phead->next;
	}

	return NULL;
}

当然这个操作在找到指定数据一次就会返回，所以在链表中要是有多个相同数据怎么办呢。

让我们到Test.c测试源文件中

//Test.c
//查找指定元素
	SLNode*pos=SListFind(sl, 2);//定义pos接收返回的结点
	while(pos) //pos找到时进入循环
	{
		printf("第%d个%d,在%p位置\n", i++,pos->data, pos);
		pos = SListFind(pos->next, 2);//找到前一个pos，从pos的下一个再继续找。
	}

通过这样的方法，我们就可以实现找到多个相同数据，然后在之后我们还会在插入和删除操作中用到它。
 

---

 

(2)、指定结点的前面插入和后面插入

指定结点前面插入新结点

//SList.c
//指定结点前面插入新结点
void SListInsert(SLNode** pphead, SLNode* pos, DateType x)
{
	assert(pphead && pos);

	SLNode* p = *pphead;
	if (*pphead == pos)
	{
		SListPushFront(pphead, x);
	}

	else
	{
		while (p->next != pos)
		{
			p = p->next;
		}

		SLNode* newnode = SListCreateNode(x);
		newnode->next = pos;
		p->next = newnode;
	}

}

因为单链表，我们知道pos位置无法直接访问pos的前面结点，所以我们需要从链表头往下遍历。（这里也明显看出单链表的缺点了）
而结点的后面插入操作我们直接就可以在pos的后面插入就行。（可以和下面的对比一下）

让我们回到Test.c测试页中

//Test.c
//插入指定元素到指定结点前
pos = SListFind(sl, 3);
while (pos) 
{
	SListInsert(&sl, pos, 10);
	pos = SListFind(pos->next, 3);
}
SListPrint(sl);

 

---

指定结点后面插入

//SList.c
//在指定结点后面插入
void SListInsertAfter(SLNode* pos, DateType x)
{
	SLNode* newnode = SListCreateNode(x);

	newnode->next = pos->next;
	pos->next = newnode;

}

后插非常简单，只需要在pos位置下一个插入就行。

测试页和前面插入的很类似

//Test.c
//插入指定元素到指定结点后O(1)
pos = SListFind(sl, 3);
while (pos) {
	SListInsertAfter(pos, 20);
	pos = SListFind(pos->next, 3);
}

 

---

 

(3)、删除指定结点

//SList.c
//删除指定结点
void SListErase(SLNode** pphead, SLNode* pos)
{
	assert(pphead);

	SLNode* p = *pphead;
	if (*pphead == pos)
	{
		SListPopFront(pphead);
	}

	else
	{
		while (p->next != pos)
		{
			p = p->next;
		}

		p->next = pos->next;
		free(pos);
	}

}

因为头(*pphead)指向第一个结点，为确保删掉第一个结点头的指向得改变，所以得分开讨论删除第一个结点和其他结点。

 

---

 

4.单链表的总结（谈单链表的缺点）：

在学习完这些单链表操作后，我们可以发现单链表有着这些缺点：

• 对比顺序表，链表不支持随机访问（用下标访问），通常需要从头指针开始找。
• 只能往下看，一旦访问到下一个结点，就不能再回头用上一个结点。
• 作为链表存储一个值同时要存储链接指针，也有一定的消耗。（但也消耗不大）
   

---

 

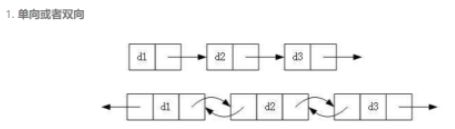
三、看看链表还有哪些结构

  除了单向链表，我们还有双向链表。
  顾名思义就是可以在当前结点访问下一个以及上一个，一个结点除了存了有效数据外，还存了访问下一个结点的地址和访问上一个结点的地址。
  我们在之后还会介绍最繁的结构双向循环有头链表。

 

---

 
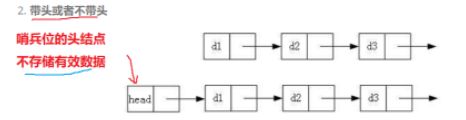
  首先我们的单链表有一个头指针（假设是指针head），这个头指针直接指向了第一个结点，并且我们的第一个结点有一个有效的值（比如我们尾插了一个1）。
  这个头指针（head）也可以一开始指向一个空结点（可以理解为里面存储一个无效的值，可以是一个不确定的随机值），这个空结点只存了访问下一个结点的地址，这个空结点也可以称为头结点、哨兵结点。
  它有两个作用（作用解释）：

1. 在有些操作下，可以不需要分头结点和其他结点的两种情况处理，可以统一一种情况处理。
2. 在函数传参可以只传一级指针。

 

---

 
  链表可以存在一个结点，让这个结点的访问地址，指向之前访问过的结点，从而构成循环链表。

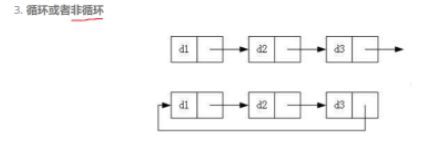
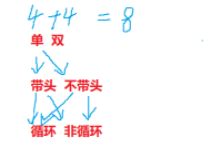
通过联系上面三种情况
一共有8中情况
而这8中情况中
最简单的结构就是：无头单向非循环链表 （作为其它数据结构的子结构，也是刚认识的单链表）
最复杂的结构就是：带头双向循环链表

四、链表和顺序表的优缺点

在通过实现链表和顺序表之后，它们到底谁更加优？
我们先来列举出它们各自的优缺点。

顺序表
优点：

1. 尾删尾插的效率高。
2. 支持随机访问（下标访问），需要随机访问结构的算法可以很好适用（比如二分查找）。
3. CPU的命中效率高。

缺点：

1. 头部和中部的删除插入效率差。O(N)
2. 连续的物理空间，空间不够就需要扩容。增容有着一定的空间浪费。

链表
优点：

1. 任意位置插入删除的效率高。O(1)
2. 按需申请空间

缺点:

1. 不支持随机访问，如果需要访问某个数据，需要遍历，并且在一些算法上不太好使用。
2. CPU的命中效率低。

有关CPU的命中效率
在计算机中，有以下这种结构。

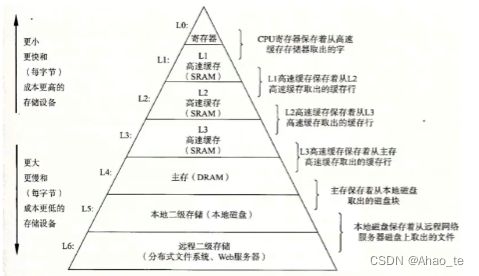
在其中，一般的数据都会在主存中存储，如果数据小的话会通过寄存器进行计算返回到写回内存，如果比较大的就会借助高速缓存。
 
假设访问存储数据的内存0x00ff1240位置，先看这个地址在不在缓存中，在就直接访问，不在就加载到缓存中，再访问。

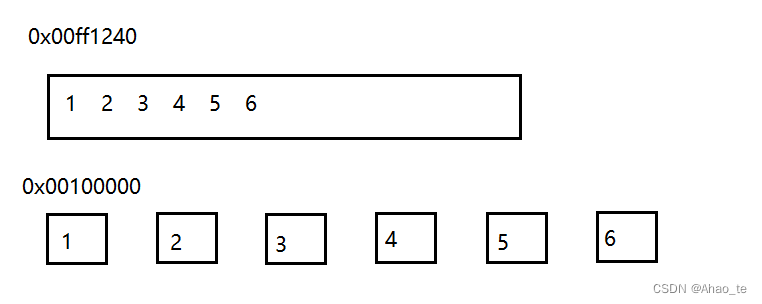
假设在第一次加载中顺序表和链表中都没命中。
由于计算机就近原则，内存访问当前位置很可能就会访问连续的位置，意味着加载顺序表中的第一个位置很可能也会加载剩下的位置，这取决于内存，比如加载了20个字节，就可能加载到5，在下次读取中，就可以直接访问，所以说顺序表命中率高。
 
链表结点地址不是完全连续的，若第一次加载20个字节，很可能就会加载到一些没用的数据，下一个结点就还需要加载，并且每次加载都会出现缓存污染，加载一些不用的数据到缓存区，而缓存区又会将不用的数据释放出去，加载了100字节，只访问了20字节，所以说链表命中率低。

所以严格来说，顺序表和链表应该是相辅相成的，并没有谁取代谁，而是在针对不同情况使用适合的结构。

五、本篇最后总结（完整代码和练习题）

  这篇总结了最简单结构的无头单向非循环链表，以及认识了一下还有哪些结构。
  以下是链表的其他内容：
  【C数据结构】从链表中看到的常见问题
  【C数据结构】解决链表最繁结构双向链表和经典力扣题
 
  以下是完整代码和本次链表练习题：
  【完整代码】：
  完整代码
  【练习题】：
  反转链表
  链表的中间结点
  链表中倒数第K个结点
  合并两个有序链表