数据结构与算法初阶1:算法的时间复杂度和空间复杂度讲解
目录
1、什么是算法的复杂度?
2、时间复杂度
3、大O的渐进表示法
4、时间复杂度算法练习
5、算法的空间复杂度
6、复杂度的OJ练习
1、什么是算法的复杂度?
我们在将算法编写成可执行程序的时候,运行时需要耗费时间资源和计算机内存(空间)资源,因此,在衡量算法的优劣需要从时间和空间两个维度来衡量,也就是本文将要介绍的时间复杂度和空间复杂度。
- 时间复杂度:其主要衡量一个算法运行的快慢问题;
- 空间复杂度:其主要衡量一个算法运行时所需要的额外空间。
目前随着计算机存储容量的快速发展,对算法空间复杂度的关注点逐步降低,人们将注意力集中在时间复杂度方面。为了掌握好一个算法的优劣性,我们有必要掌握如何判断算法的复杂度问题,从而在今后的工作学习中,根据实际的需求选择出或写出最优算法。
2、时间复杂度
在计算机科学中,时间复杂度是一个函数,它定量的描述了该算法的运行时间。但我们知道算法的运行时间在不同的硬件设备上运行时,会得到不同的结果,即在硬件好的平台上运行,同一个算法的运行时间和较差的硬件运行相比耗时很少。为此,我们需要换一种时间复杂度的分析方式:一个算法所花费的时间与其中语句的执行次数成正比,算法中的基本操作的执行次数,即为算法的时间复杂度。
通俗来讲,就是在算法中找到某条基本语句与问题规模N之间的数学表达式,也就可以算出该算法近似的时间复杂度。
下面我们先来看一个例子,感受时间复杂度在算法中是如何识别出来的:
#define _CRT_SECURE_NO_WARNINGS
#include
void Func(int N)
{
int count = 0;
for (int i = 0; i < N; i++)
{
for (int j = 0; j < N; j++)
{
++count;
}
}
for (int k = 0; k < 2 * N; k++)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
}
int main()
{
//写一个统计次数的Func函数
Func(10);
return 0;
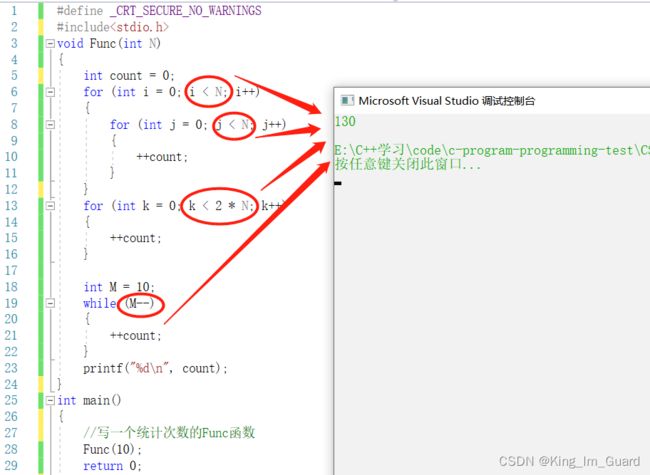
} 从上图分析中,我们可以看出,函数Func中包含有四个循环,然后利用count计数,在该函数中经历的每一次循环都是时间上的叠加,Func函数执行的基本操作次数为:
| Func(N)=N^2+2*N+10 |
上述表达式表示的是Func函数在执行过程中具体的执行次数,但当我们遇到很复杂的函数时,这是准确的执行次数是不可行的,为此,我们一般采用简化的方式,只需要能大概表示出执行次数,在这里将引出另一个概念:大O的渐进表示法。
3、大O的渐进表示法
| 符号O:用来描述函数渐进行为的数学符号 | |
| 推导大O阶的方法 | 1、用常数1取代运行时间中的所有加法常数 |
| 2、在修改后的运行次数函数中,只保留高阶项 | |
| 3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数,得到的结果就是大O阶。 | |
| 上例中的函数Func的时间复杂度为:O(N^2) | |
注:在上述的分析中,我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行的次数。
| 另:有些算法的时间复杂度存在最好、平均和最坏的情况: |
| 时间复杂度最好情况:任意输入规模的最小运行次数(下界) |
| 时间复杂度平均情况:任意输入规模的期望运行次数 |
| 时间复杂度最坏情况:任意输入规模的最大运行次数(上界) |
| 例如:在一串长度为N的数组中搜索一个数据x,最好情况:1次找打;平均情况:N/2次找到;最坏情况:N次找到(即把数组中的数据全部遍历完,可能找到,也可能没找到)。 |
4、时间复杂度算法练习
//计算Func2函数的时间复杂度?
void Func2(int N)
{
int count = 0;
for (int k = 0; k < 2 * N; ++k)
{
++count;
}
int M = 10;
while (M--)
{
++count;
}
printf("%d\n", count);
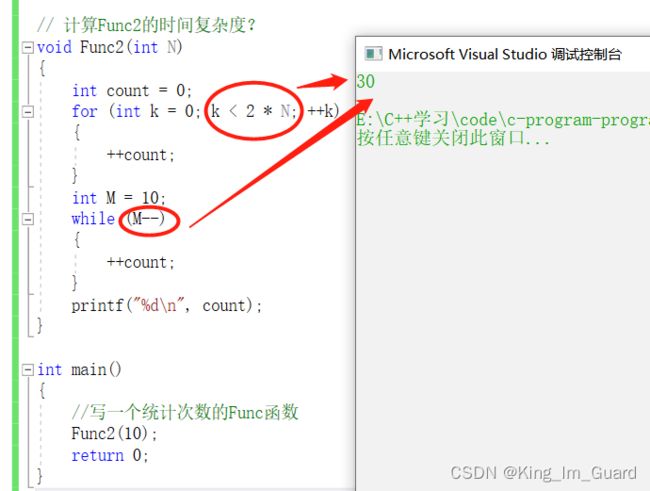
}| Func2(N)=2*N+10,时间复杂度O(N) |
// 计算Func3的时间复杂度?
void Func3(int N, int M)
{
int count = 0;
for (int k = 0; k < M; ++k)
{
++count;
}
for (int k = 0; k < N; ++k)
{
++count;
}
printf("%d\n", count);
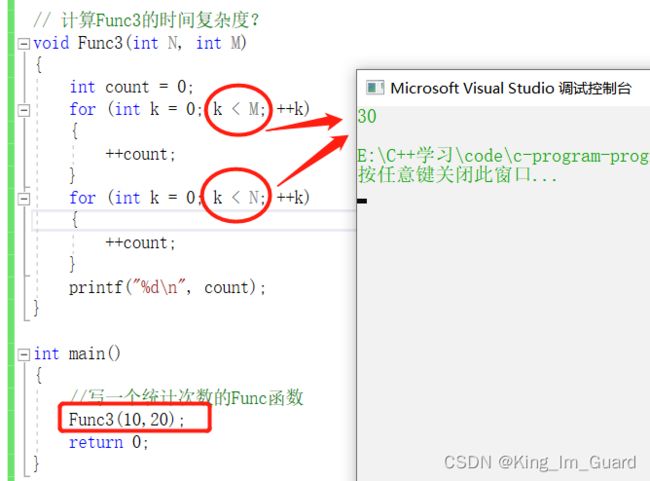
}| Func3(N,M)=N+M,时间复杂度O(N+M) |
// 计算Func4的时间复杂度?
void Func4(int N)
{
int count = 0;
for (int k = 0; k < 100; ++k)
{
++count;
}
printf("%d\n", count);
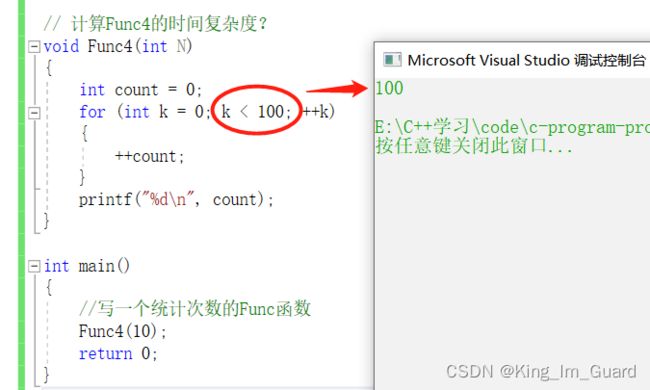
}| 函数Func4(N)内部执行次数与N无关,执行次数为常数次100,根据大O的渐进表示法1,其时间复杂度O(1) |
// 计算BubbleSort的时间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}| BubbleSort函数为冒泡排序函数,如果严格按照我们前面分析的从循环次数角度计算时间复杂度,则: F(N)=N-1+N-2+N-3+...+2+1=((N-1)+1)*(N-1)/2 (利用等差数列公式)。 其具体的时间复杂度为:F(N)=N*(N-1)/2, 根据大O的渐进表示法,实际中其时间复杂度表示为: 1、最好情况:遍历数组一遍,O(N); 2、最坏情况:遍历完数组中所有元素,可能找到,可能没找到,时间复杂度O(N^2) |
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{
assert(a);
int begin = 0;
int end = n - 1;
// [begin, end]:begin和end是左闭右闭区间,因此有=号
while (begin <= end)
{
int mid = begin + ((end - begin) >> 1);
if (a[mid] < x)
begin = mid + 1;
else if (a[mid] > x)
end = mid - 1;
else
return mid;
}
return -1;
}| BinarySearch为二分查找函数,可理解为折半查找(可借助将纸折叠理解),假设折半查找了N次,则具体的执行次数可理解为:1*2*2*2....2*=N,可以推出:2^x=N.........x=log2(N)。 所以最坏的时间复杂度为:O(log2N) ,可能找到,可能找不到;最好的时间复杂度为:O(1) 比较O(N)和O(log2(N)) N= 1000 1000000 10亿 O(N)= 1000 1000000 10亿 O(log2(N))= 10 30 30 从这里分析可以看出,二分查找函数具有很大的优势,但前提是需要先排好序,这样才可以调用此函数。 |
// 计算阶乘递归Fac的时间复杂度?
long long Fac(size_t N)
{
if (0 == N)
return 1;
return Fac(N - 1)*N;
}| 递归方式:F(N)---F(N-1)---F(N-2)---F(N-3)---F(2)---F(1)---F(0) 此时可以知道具体的时间复杂度为:O(N+1),大概的时间复杂度为:O(N)。 |
// 计算斐波那契递归Fib的时间复杂度?
long long Fib(size_t N)
{
if (N < 3)
return 1;
return Fib(N - 1) + Fib(N - 2);
}| 斐波那契额递归方式: F(N) F(N-1) F(N-2) F(N-2)---F(N-3) F(N-3)---F(N-4) F(2)---F(1) ------------------------------- 此时可近似认为:2^0+2^1+2^2+2^3+...+2^(N-2)=2^(N-1)-1 此时可以知道时间复杂度为:O(2^N)。 |
看到这里,相必读者们应该对算法时间复杂度的求解有了一定的认识与理解,那么接下来我们探讨算法的空间复杂度问题。
5、算法的空间复杂度
空间复杂度是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度。空间复杂度同时间复杂度一样,不完全是计算程序占用了多少字节,而是计算的变量的个数,同样使用大O的渐进表示方法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时显式申请的额外空间来确定。
下面我们通过案例感受一下算法中的空间复杂度求解问题:
// 计算BubbleSort的空间复杂度?
void BubbleSort(int* a, int n)
{
assert(a);
for (size_t end = n; end > 0; --end)
{
int exchange = 0;
for (size_t i = 1; i < end; ++i)
{
if (a[i - 1] > a[i])
{
Swap(&a[i - 1], &a[i]);
exchange = 1;
}
}
if (exchange == 0)
break;
}
}分析:以冒泡排序算法为例,函数创建的变量主要为图中所圈部分,按照大O的渐进表示方法,其空间复杂度为常数项,所以写为O(1)。
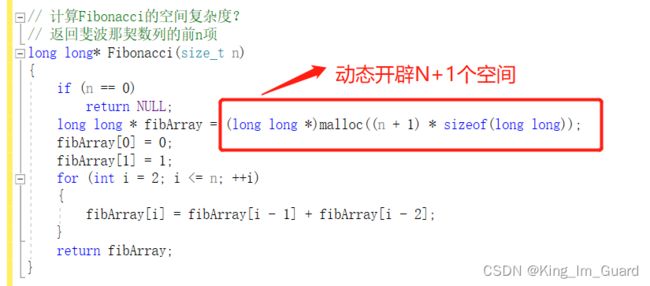
// 计算Fibonacci的空间复杂度?
// 返回斐波那契数列的前n项
long long* Fibonacci(size_t n)
{
if (n == 0)
return NULL;
long long * fibArray = (long long *)malloc((n + 1) * sizeof(long long));
fibArray[0] = 0;
fibArray[1] = 1;
for (int i = 2; i <= n; ++i)
{
fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
}
return fibArray;
}分析:以斐波那契算法为例,函数创建的变量主要为图中所圈部分,利用malloc函数动态开辟N+1个空间,按照大O的渐进表示方法,其空间复杂度表示为O(N)。
// 计算阶乘递归Fac的空间复杂度?
long long Fac(size_t N)
{
if (0 == N)
return 1;
return Fac(N - 1)*N;
}分析:Fac递归函数创建的变量主要为Fac(N)-Fac(N-1)-Fac(N-2)--..--Fac(1)-Fac(0),利用递归调用了N次,开辟了N个栈帧,按照大O的渐进表示方法,其空间复杂度表示为O(N)。
6、复杂度的OJ练习
练习1:面试题 17.04. 消失的数字 - 力扣(LeetCode)
int missingNumber(int* nums, int numsSize){
int x=0;
//利用按位异或,相同为0,相异为1,首先数字0分别与数组中的每一个元素异或,然后再与1-numsSize个数字异或,这样可以使得重复出现的数字异或为0,最终的结果就是缺失的数字。
for(int i=0;i分析:时间复杂度为0(N),空间复杂度为O(1),因为并没有开辟多余的空间。
练习2:189. 轮转数组 - 力扣(LeetCode)
void reverse(int*nums,int start,int end)
{
int tmp=0;
while(start分析:利用三段逆序分析方法,时间复杂度为O(N) ,空间复杂度为O(1)。
| 例如:1 2 3 4 5 6 前n-k个逆置:3 2 1 4 5 6 后k个逆置:3 2 1 6 5 4 整体逆置:6 5 4 3 2 1 |
至此,算法的时间复杂度和空间复杂度问题分析到这里,希望为读者带来不错的阅读体验,后续数据结构与算法学习内容持续更新中.。。。。。。