[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-
论文原文:Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for biological and healthcare applications - ScienceDirect
论文全名:Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for biological and healthcare applications
论文代码:GitHub - mullakaeva/GiG: Graph-in-Graph (GiG)
英文是纯手打的!论文原文的summarizing and paraphrasing。可能会出现难以避免的拼写错误和语法错误,若有发现欢迎评论指正!文章偏向于笔记,谨慎食用!
目录
1. 省流版
1.1. 心得
1.2. 论文框架图
2. 论文逐段精读
2.1. Abstract
2.2. Introduction
2.3. Related work
2.4. Method
2.4.1. Graph-in-graph model
2.4.2. Node degree distribution loss (NDDL)
2.5. Experiments and results
2.5.1. Datasets
2.5.2. Implementation details
2.5.3. Quantitative results
2.5.4. Knowledge discovery analysis
2.6. Discussion
2.7. Conclusion
3. 知识补充
3.1. Upstream and downstream
3.2. Soft threshold
3.3. Soft assignment and hard assignment
3.4. CATH
4. Reference List
1. 省流版
1.1. 心得
(1)开头说图是适用非欧几里得空间,的确是这样因为基本脑图ROI之间的边都不是按距离算的。但是意思就是默认了每个脑区的功能一定隔得那么开是吗...如果和距离其实有关系呢?脑区一定就像各个器官一样分离吗?还是说其实呈扩散状呢
(2)都是2023的论文了为什么老强调非欧几里得
(3)数学部分真是...简略,行吧可能是重点放在NDDL上了
(4)救命这个表格分析真是over specific
(5)Again神奇排版
(6)可解释性的图好清晰
1.2. 论文框架图
2. 论文逐段精读
2.1. Abstract
①Graph structure beyonds the traditional Euclidean space and distance
②Therefore, graph representation is suitable for brain connetome analysis and molecule property prediction
③The authors put forward Graph-in-Graph (GiG) with Node Degree Distribution Loss (NDDL) to classify protein and brain image
2.2. Introduction
①Graph representation is used in CV, CG, physics, chemistry and medicine recently
②Most graph model takes individual graph input, then aggregates neighbors (nodes or edges) to a new graph
2.3. Related work
(1)Protein classification (enzymes or non-enzymes)
①SVM
②C-SVM
③GCNNs
④GNN
(2)Brain connectome analysis
①Brain graph prediction: Kullback–Leibler (KL) divergence
②Brain graph integration/fusion: multi-view graph normalizer network (MGN-Net)
③Brain graph classification (multi-graph/multi-modal classification): MICNet, GNN selection (RG-Select), DMBN, rs-fMRI-GIN, Graph Isomorphism Network (GIN), BrainNetCNN, ElasticNet, ST-GCN, DECENNT
(3)Molecular toxicity prediction (drug discovery)
①DNNs
②Tree-based ensemble methods
③Simplified Molecular-Input Line-Entry (SMILES)
④Bridging works
⑤Graph Multiset Transformer (GMT)
(4)GCNNs in different areas:
①Social sciences
②CV and CG
③Physical
④Medical/biological sciences
(5)Methods of GiG:
①Fully inductive
②Not neccesary for test data
toxicology n.毒理学;毒物学 enzyme n.酶 proliferation n.增殖;激增;涌现;大量的事物
2.4. Method
There are ![]() graphs,
graphs, ![]() and each
and each ![]() ;
;
![]() denotes node/verticle,
denotes node/verticle, ![]() denotes edge,
denotes edge, ![]() denotes node feature matrix,
denotes node feature matrix, ![]() denotes the number of features;
denotes the number of features;
the output for each graph is a vector ![]() , which indicates the propability of prediction;
, which indicates the propability of prediction;
![]() denotes the number of possible classes;
denotes the number of possible classes;
2.4.1. Graph-in-graph model
GiG framework:
where ![]() caculates graph features,
caculates graph features, ![]() learns latent connections between graphs,
learns latent connections between graphs, ![]() combines
combines ![]() and
and ![]() to predict
to predict
(1)Node-level module F_1
①Graph feature vector ![]() , where
, where ![]() denotes GCNN and pooling operators
denotes GCNN and pooling operators
②Graph feature matrix ![]() (我倒是一直没有get到这种玩意儿,文中说
(我倒是一直没有get到这种玩意儿,文中说![]() 是1*H维的,那不是行向量吗,
是1*H维的,那不是行向量吗,![]() 又横向拼接行向量吗?我这里竖着拼接了,我不知道对不对我现在还没看到代码。我猜1*H是列向量,因为下面的N维是行向量)
又横向拼接行向量吗?我这里竖着拼接了,我不知道对不对我现在还没看到代码。我猜1*H是列向量,因为下面的N维是行向量)
(2)Population-level module F_2
①The input of ![]() is the output of
is the output of ![]()
②Function in this layer: ![]() ,
,
where each ![]() ,
, ![]() ,
, ![]() and
and ![]() are learnable soft-threshold and temperature parameters
are learnable soft-threshold and temperature parameters
③ ![]() represents the weighted adjacency matrix
represents the weighted adjacency matrix
(3)GNN classifier F_3
①The final function:
(这我自己写的,他竟然只有语言描述啊)
2.4.2. Node degree distribution loss (NDDL)
①They proposed a regularizer, Node Degree Distribution Loss (NDDL) based on Kullback–Leibler divergence between computed degree distribution and target distribution (Gaussian distribution is chosen). Divergence of value between LGL and LGL+NDD:
②The overall steps:
③![]() denotes a adjacency matrix of undirected graph and
denotes a adjacency matrix of undirected graph and ![]() denotes a weighted fully connected graph. They only retain edges with which weights are greater than 0.5:
denotes a weighted fully connected graph. They only retain edges with which weights are greater than 0.5:
![]()
where each node degree vector in it (sum of each row combines a new row vector):
![]()
④Computing the soft assignment matrix ![]() :
:
where ![]() is a hyperparameter which set to 0.6;
is a hyperparameter which set to 0.6;
![]() ;
;
![]() denotes possible degree
denotes possible degree
⑤Node degree distribution ![]() is calculated by:
is calculated by:
(他这个下面表达式我觉得有点小问题啊,算出来其实应该是两个Σ,因为他明显是把矩阵所有值求和了。还是说这样表述在数学里面是对的呢?)
⑥The final DNNL step:
![]()
where ![]() denotes target normal discrete distribution with learnable parameters
denotes target normal discrete distribution with learnable parameters
⑦The loss function:
![]()
where ![]() is the cross entropy loss;
is the cross entropy loss;
![]() represents the class membership indicator (1 represents belonging to, 0 is not);
represents the class membership indicator (1 represents belonging to, 0 is not);
![]() denotes the probability of predicted class
denotes the probability of predicted class
2.5. Experiments and results
(1)Dataset information
①Statistics of dataset:
②Class distribution:
(2)Experiment settings
①They test GiG in biological, medical and chemical domains
②Each sample is a graph
③They test 2 variants, LGL and LGL+NDD
2.5.1. Datasets
①Predict sex from brain fMRI data in the Human Connectome Project (HCP)
②Classify proteins as enzymes or non-enzymes in PROTEINS
③Predict binary value 0/1 as not active/active of toxicity
(这里我没有写很详细,作者其实写了很多)
2.5.2. Implementation details
(1)Settings
①Optimizer: Adam
②Activation: ReLU, except KNN in HCP which adopts Sigmoid following with batch norm
③DL framework: PyTorch and PyTorch Geometric
(2)Dataset split
①Training set is 72%, validation set is 8%, test set is 20% in HCP
②90% training set and 10% test set in PROTEINS_29, and training set is divided into training and validation sets through 10-folds
③Predefined scaffold splits are used for Tox21
(3)Importance of batch size
①They tested 1 batch and all batches
②Larger batch brings better performance, hence they suggest to combine test and traning samples
scaffold n.脚手架;断头台; 鹰架;绞刑架;建筑架
2.5.3. Quantitative results
①Comparison of classifying models:
②Comparison of recent models on HCP:
where G is GroupICA, S is Shaefer, M is multi-modal parcellation
③Comparison of different folds:
④They test the relationship between number of test sets and accuracy:
where triangles denotes mean value and the data comes from PROTEINS_3
⑤Distribution of degrees before and after adopting 0.5 threshold:
where the x-axis is the node degree, and the y-axis denotes occurrence of nodes in its x-axis degree in PROTEIN_29
2.5.4. Knowledge discovery analysis
①Population graphs comparison in HCP, with red outline representing misclassified:
it is easy to see GLG+NDD clusters better
②Population graphs comparison in PROTEINS_29:
where threshold for LGL is 0.01, for LGL+NDD is 0.5. In addition, (b) and (d) implement CATH classes, i.e. classifying "mainly belongs to a", "mainly belongs to b", "combination of a and b"
③Population graphs comparison of GiG LGL+NDD in different datasets:
where threshold for LGL+NDD is 0.5
④The influence of ![]() where the first row is LGL and the second row is LGL+NDD on PROTEINS_3:
where the first row is LGL and the second row is LGL+NDD on PROTEINS_3:
⑤
⑥Population graph evaluation:
⑦Evaluation of learned ![]() :
:
⑧Hyperparameters optimizing with "bs" represents batch size, "k" represents number of KNN graph, "S" represents scheduler, DECL denotes DynamicEdgeConv(ReLu(Linear(2*–,–))), "-" denotes dimension from the previous or subsequent layer, "P" represents Reduce Learning Rate on Plateau, "C" represents Cosine Annealing
⑨Hyperparameters selection ranges
2.6. Discussion
①They designed two learnable parameters: ![]() and
and ![]() , which
, which ![]() can significantly influence the classifying results
can significantly influence the classifying results
②Proper input-graph representations also greatly impact
③Limitations: 1) target distribution in NDDL, 2) different ![]() and
and ![]()
2.7. Conclusion
They proposed a graph structure learning method includes node-level, population-level, and GCN classifier
3. 知识补充
3.1. Upstream and downstream
(1)Upstream tasks mainly represent pre-training
(2)Downstream tasks usually denote the rest model part
3.2. Soft threshold
相关链接:软阈值(Soft Thresholding)函数解读-CSDN博客
3.3. Soft assignment and hard assignment
(1)Soft assignment: only presents the probability of classifying
(2)Hard assignment: gives the specific cluster of one data
3.4. CATH
(1)Explanation: Class(C), Architecture(A), Topology(T) and Homologous superfamily (H) of protein
(2)CATH classes:
4. Reference List
Orengo, C. et al. (1997) 'CATH – a hierarchic classification of protein domain structures', Structure, vol. 5, issue 8, pp. 1093-1109. doi: Redirecting
Zaripova, K. et al. (2023) 'Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for biological and healthcare applications', Medical Image Analysis, vol. 88, 102839. doi: Redirecting
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第1张图片](http://img.e-com-net.com/image/info8/0a303ea0aec04dbabb710f60d3e76123.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第2张图片](http://img.e-com-net.com/image/info8/b23131cee74e4816a3d40fb00a313ca5.jpg)
![p=F_{3}\left ( h,A_{p} \right )=\left [ p_{1},...,p_{N} \right ]\\\\=shared\,\, weights\, \, and\, \, ReLU(GCNs\left ( h,A_{p} \right ))](http://img.e-com-net.com/image/info8/d94b06ef99f14a738308dd13aa50923e.png)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第3张图片](http://img.e-com-net.com/image/info8/7420f65fba334c8e95cc1568d3003bed.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第4张图片](http://img.e-com-net.com/image/info8/306f988aa49f4ddaa062c8fc331f171c.jpg)
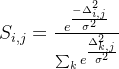
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第5张图片](http://img.e-com-net.com/image/info8/892c9972e6a848d38a97702d66cea705.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第6张图片](http://img.e-com-net.com/image/info8/fd8fe8b7dec345dfb581b515c8eebb37.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第7张图片](http://img.e-com-net.com/image/info8/9661dead42c642618ef41e8eb8f463bb.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第8张图片](http://img.e-com-net.com/image/info8/a3ee81090f4944289f7a96d6b5c8f67f.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第9张图片](http://img.e-com-net.com/image/info8/c003240840154f50b63b5c92e774a286.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第10张图片](http://img.e-com-net.com/image/info8/7784e9e775524b44aead944af124caf1.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第11张图片](http://img.e-com-net.com/image/info8/ad1cc5941cfe4b509976f171f3cee799.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第12张图片](http://img.e-com-net.com/image/info8/7aca8b03665f42d6b3de4f4c9627cdde.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第13张图片](http://img.e-com-net.com/image/info8/0b39d40e6e084b8589c3d1a5490b98b8.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第14张图片](http://img.e-com-net.com/image/info8/0ad14a99456d4d338b7b1a927d069273.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第15张图片](http://img.e-com-net.com/image/info8/60bb7339e6cd4da6a854147eebef4067.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第16张图片](http://img.e-com-net.com/image/info8/62618f4067c34ef486c76142436a47a9.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第17张图片](http://img.e-com-net.com/image/info8/a68dfef3332b40d19ae9abc22b54d380.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第18张图片](http://img.e-com-net.com/image/info8/434c36b51a004a1ab86ccb793b25fbb7.jpg)
![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第19张图片](http://img.e-com-net.com/image/info8/abe92c5f1df24b2b8c21f982b3ab9877.jpg)

![[论文精读]Graph-in-Graph (GiG): Learning interpretable latent graphs in non-Euclidean domain for bio-_第20张图片](http://img.e-com-net.com/image/info8/40fb468c2708436ca69c478126f47f57.jpg)