由递推关系式用差分方程的方法得到通项公式实现求斐波那契数列的第n项;迭代、递归、栈、差分方程之间的本质联系以及由推广的迭代法解决“变态青蛙跳台阶”问题;汉诺塔问题的数字特征以及用递归解决的原理推导。
最近几天在研究算法中一个比较基础且突出的问题,就是关于“递推关系式、递归、迭代、序列前k项和”之间的区别与联系。
一、斐波那契数列与差分方程
首先我们考察一个经典的算法,求斐波那契数列的第n项。C语言的简单算法最常见也最简单的就是“递归实现”与“迭代”实现,网络上这样的代码也很多,比比皆是,在这个第一个环节关于“递归”和“迭代”先给出实现代码,原理我们放到文章偏后处讲解。
斐波那契数列:是这样一个数列,它的初始的两个值F[0]=0,F[1]=1,之后每一项等于它前两项之和即F[n]=F[n-1]+F[n-2],n>=2的自然数。
即:0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610...
//F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2),n>=2的自然数
下面我们来介绍一下”差分方程“,首先我们要明确差分方程主要解决的是哪一类问题。先来告诉大家,在数列研究中的一个比较突出的焦点问题就是给定数列中任意三项之间的递推关系,让你求这个数列的通项公式。比如说斐波那契数列的三项间的递推关系是F[n]=F[n-1]+F[n-2],我们下面就以斐波那契数列的递推关系为例来进行一次用差分方程的方法解决求通项公式的问题。
差分方程:
差分方程的解题步骤可以把它看作离散情况下的二阶常系数齐次微分方程的解法:
以上我们可以联系二阶常系数齐次微分方程的解法作对比(这里有高等数学基础的朋友可能比较容易接受一点):
我们注意到以上在特征方程△<0时的解为虚数,不过我们现在用差分方程求通向公式研究的问题是暂时局限在自然数范围内的,如果这个数列的递推关系用差分方程的方法得到的解在复数域中我们暂时在本篇文章中先不讨论,我会给出相应△<0时应该输出的代码,在我的其他文章中我会专门来讨论复数表达的问题届时我会在本篇文章放上超链接,我先来提一下,感兴趣的朋友可以沿着我给的线索进行进一步的学习。![]() ,这个欧拉公式是单位复向量的表达式,即可以用左边那一个玩意儿表达右边实部为a=cos
,这个欧拉公式是单位复向量的表达式,即可以用左边那一个玩意儿表达右边实部为a=cos![]() ,虚部为b=sin
,虚部为b=sin![]() 的复数,我两边乘以
的复数,我两边乘以![]() (就是复向量的模长r)就可以得到复平面内任意一个复数。不用担心符号的问题,因为
(就是复向量的模长r)就可以得到复平面内任意一个复数。不用担心符号的问题,因为![]() =-1,
=-1,![]() =1,考察
=1,考察![]() 、cosx、sinx展开式作对比,这里不再赘述。
、cosx、sinx展开式作对比,这里不再赘述。
我们在用差分方程解决由数列中三项之间的递推关系求通项公式的时候主要情况聚焦在△>0和△=0的部分,下面我给出斐波那契数列通项公式用差分方程方法的数学推导过程:
那么很显然,有公式可以用C语言的顺序程序设计实现求斐波那契数列的第n项
但是,这并不是我们的目的,我们的目的是能够做到“给数列中任意k个数之间的递推关系,求得它们得第n项是多少”,可以用差分方程的方法实现,但是差分方程的方法有局限性,它顶多可以解决给定4个及4个以内序列内数之间的递推关系求得通项公式的表达式,根本原因在于五次以上方程无实数解,再用差分方程的方法没有意义。
但是我们就这个问题继续谈一谈数列中三项间递推关系求通项公式的焦点问题,我能不能实现输入待求解序列的两个初始值,与差分方程的解法进行对比,输入三项间递推关系标准化后对应差分方程解法的a和b(就是对递推关系移项让右边变为0且将下标最高项的系数变为1,比如F[n]=F[n-1]+F[n-2]标准化为F[n]-F[n-1]-F[n-2]=0,那输入的就是a=-1 b=-1),让计算机帮我们解这个差分方程?
那么下面紧接着就是我给出的含输入的初值F1、F2、输入的对应系数a、b由差分方程求解得到的公式的数学推导(不会克拉默法则的用高斯消元或者初等变换求线性方程组的方法一样可以得到,这里由感兴趣且不会克拉默法则的读者自行完成,由于我们解决的数列中三项间递推关系求通项公式的问题的时候,我们一定至少知道数列中最前面两个初值,所以在用差分方程的方法求通项公式的时候解的方程的次数一定和下面的这些方程的次数一致,即步骤一定相同,故对我们提出来的需求“给数列中三项间的递推关系式,输入的初值F1、F2、输入的对应系数a、b由差分方程求解通项公式”有可行性。):
那么下面紧接着给出代码实现“给数列中三项间的递推关系式,输入的初值F1、F2、输入的对应系数a、b由差分方程求解通项公式”:
用差分方程方法求解由数列中三项间的递推关系式求通项公式的算法的头文件:
“Fibonacci.h”
#ifndef FIBONACCI_H_INCLUDED
#define FIBONACCI_H_INCLUDED
#define PI 3.1415926
#include
#include
// 0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610...
//F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2),n>=2的自然数
int Fibonacci_by_recursion_formula(int n)
{//Fibonacci是使用无理数表示有理数的典例
if(n == 0) //定义初始值
return 0;
if(n == 1 || n == 2)
return 1;
double c1,c2,x1,x2;
double deta;
double a,b;
double F1,F2;
printf("请输入序列的前两项\n");
printf("如果是斐波那契数列请务必输入F1=1,F2=1:");
printf("\nF1=");scanf("%lf",&F1);
printf("F2=");scanf("%lf",&F2);//这边格式输入一定要注意不能习惯于用%d,而应该用%lf!
printf("请考察已知序列三项间关系的递推关系式中对应差分方程中的a和b并输入a和b\n");
printf("如F(n)=F(n - 1)+F(n - 2),\n标准化为F(n)-F(n - 1)-F(n - 2)=0则应输入a=-1,b=-1");
printf("\n请输入a:");scanf("%lf",&a);
printf("请输入b:");scanf("%lf",&b);//这边格式输入一定要注意不能习惯于用%d,而应该用%lf!
deta=a*a-4*b;
if(F1==1&&F2==1&&a==-1&&b==-1)printf("是斐波那契数列!\n");
else printf("不是斐波那契数列!\n");
if(deta>0)
{
x1=((-a)+sqrt(deta))/2;
x2=((-a)-sqrt(deta))/2;//由递推关系F(n)=F(n - 1)+F(n - 2)通过求解差分方程的特征方程得到的特征方程的两个解
c2=(F2-x1*F1)/(x2*x2-x1*x2);//差分方程的阶数比较低,一定可以用克拉默法则求解,也一定是用前两项进行求解C1和C2,n一定是1次和2次,故可形成公式
c1=(F1*x2-F2)/(x1*x2-x1*x1);//由克拉默法则得到的表达式!
int Fib_n=c1*pow(x1,n)+c2*pow(x2,n);//保留差分方程的解的形式保持一致
return Fib_n;//只能算到第46个斐波那契数列,如果有需要,则需改变数据类型
}//如何用C实现真正的矩阵运算?
else if(deta==0)
{
x1=-a/2;
x2=-a/2;
c1=(4*F2+2*a*F1)/(a*a);
c2=-(4*a*F1+4*F2)/(a*a);//克拉默法则求得的公式
int Fib_n=(c1+c2*n)*pow(x2,n);//保留差分方程的解的形式保持一致
return Fib_n;//只能算到第46个斐波那契数列,如果有需要,则需改变数据类型
}
else
{
double x;//弧度制角度,复向量的角度
double m,k;
m=-a/2;//实部
// complex double i = _Complex_I;//不需要用到内置复数数据类型
k=sqrt(fabs(deta))/2;//虚部,先求deta的绝对值,再进入根号下,求绝对值用fabs而不是abs
// x1=m+k*i;
// x2=m-k*i;
// printf("%f+%fi\n",m,k);
double r,val;//r是复数的模,val是辅助三角函数运算的值弧度值转角度制
val=180.0/PI;
r=sqrt(m*m+k*k);
x=atan(k/m)*val;//求复向量的角度
printf("Fn=pow(r,n)*(c1*cos(x*n)+c2*sin(x*n))\n");
printf("其中r=%lf ,x=%lf,n=%d\n",r,x,n);
printf("c1=(F1*sin2x-F2*sinx)/(r*(cosx*sin2x-sinx*cos2x)\nc2=(F2*cosx-F1*cos2x)/(r*(cosx*sin2x-sinx*cos2x)");
return -1;//就单纯的差分方程来讲,返回值这里的代码是不健壮的,但就斐波那契数列来讲,返回值这里是健壮的。
}
}
#endif // FIBONACCI_H_INCLUDED
main函数:
#include
#include
#include "Fibonacci.h"
// 0,1,1,2,3,5,8,13,21,34,55,89,144,233,377,610...
//F(0)=0,F(1)=1, F(n)=F(n - 1)+F(n - 2),n>=2的自然数
int main()
{
int n;
printf("请输入您要计算的数列中的第n项:");
scanf("%d",&n);
//使用通项公式计算F(n)
int Fn=Fibonacci_by_recursion_formula(n);
printf("用通项公式计算该数列中的第%d项为:%d\n",n,Fn);
} 测试结果:
有人会问了,你为什么那边返回-1?就是因为我原本对于这个算法是仅仅想让帮我计算斐波那契数列的差分方程然后给我返回斐波那契数列的第n项的,如果说输入特征方程的△<0其实我们根本不用考虑(在△<0这里如果算法上有优化或者计算上有错误欢迎指点,这里我没有细细验证,因为差分方程的方法不是用计算机解决这类问题的主流方法。)
下面我来再举个例子讲一下差分方程在我们在线性代数中求n阶行列式的值的时候的应用场景:
其实我们届时也可以再总结一下我们高中的时候给定数列间的常见的递推关系求通项公式的方法,以备我们后续快速实现:
由递推关系求通项公式的常用方法:(都是为了能够和最开始的几项(低阶)发生关系)
作差求和、作商求和、逐差法、逐项相乘、取倒数法、开平方法、待定系数法、数学归纳法...
附加:求前n项和的方法:
倒序相加(等差)、错位相减(等比)、累差法、累乘法、裂项相消、 分组求和...
二、“给定数列中任意k个项(4<=k
我们由上面讨论的第一个大问题也是数列研究中的一个核心的焦点问题就是关于数列中三项间递推关系求通项公式的问题,我们也了解到了差分方程求通向公式的局限性(只能求解由四项以内的项之间递推关系求通项公式)我们引发思考,有什么样的方法可以不用通项公式,退一步不用笔算,循环的操作用编程实现,时间复杂度控制在O(n)级别的算法让计算机来实现给定数列中任意k个项(4<=k
还以斐波那契数列作为引入,先给出大家都知道的求斐波那契数列第n项的迭代实现,紧随其后我将解释这些过程当中发生了什么变化,设计这个算法时候的思想是什么:
//斐波那契迭代实现
int Fibonacci_by_iteration(int n)
{
if(n == 0) //定义初始值
return 0;
if(n == 1 || n == 2)
return 1;
int a=1,b=1,c=0; //定义初始值
//用一个for循环,a、b分别为前两项,c为前两项之和,得到c后进行交换更新a、b的值,进行n次交换即可。
for(int i=3;i<=n;i++) //更新操作
{
c = a+b;//从F(3)=F(1)+F(2)开始,相当于由上一步的结果得到F(n),这就叫迭代
a = b;//下一步的a=F(2)
b = c;//下一步的b=F(3)
}
return c; //c即为结果输出
}
int main()
{
//迭代法计算F(n)
printf("用迭代法计算斐波那契数列中的第%d项为:%d\n",n,Fibonacci_by_iteration(n));
return 0;
}以上是两个变量不断在更迭换代参加工作,对于每一轮循环更加核心的代码c=a+b;a位置相当于老年人,b位置相当于年轻人,下一轮a位置为上一轮的b位置的年轻人,接替了上一轮a位置老者的工作,上一轮产生的c放到这一轮的b位置以年轻血液参加工作,那么我们再往下探寻,三个变量的更迭换代该是一个什么样的过程?如下图:
那么我们再来看普通青蛙跳台阶问题:
问题描述:
一只青蛙可以一次跳 1 级台阶或一次跳 2 级台阶,例如:跳上第一级台阶只有一种跳法:直接跳 1 级即可。跳上两级台阶,有两种跳法: 每次跳 1 级,跳两次; 或者一次跳 2 级.问要跳上第 n 级台阶有多少种跳法?
先考察跳第一级台阶共几种跳法?很显然1种
(以下的“+”为加法原理的意思)
考察第二级台阶几种方法?
case1:跳一级到第一级台阶+跳1级到第二级台阶
case2:跳两级到第二级台阶
共2种方法
考察第三级台阶共几种方法?
case1:均跳1级
case2:前两级采用跳两级的方式+后一级跳一级
case3:第一级采用跳一级方式+后两级采用跳两级的方式
共3种方法
考察第四级台阶共几种方法?
case1:均跳一级
case2:跳两次两级
case3:第一次跳两级到第二级+第二次跳一次一级到第三级+第三次跳一次一级到第4级
case4:第一次跳一次一级到第一级+第二次跳一次二级到第三级+第三次跳一次一级到第4级
case5:第一次跳一次一级到第一级第二次跳一次一级到第二级+第三次跳一次二级到第4级
...继续往下会发现普通青蛙跳台阶问题,第n级台阶共几种跳法=前两级台阶跳法之和,即满足初始值F[1]=1,F[2]=2的斐波那契数列的递推关系式F[n]=F[n-1]+F[n-2]。
那么划归到这个问题就好办了,就是改变一下输入到上面迭代实现斐波那契数列的初值为F[1]=1,F[2]=2到代码当中就实现了普通青蛙跳台阶问题的求解。
代码实现:
//斐波那契迭代实现
int Fibonacci_by_iteration(int n)
{
double F1,F2;
printf("请输入序列的前两项\n");
printf("如果是斐波那契数列请务必输入F1=1,F2=1:");
printf("\nF1=");scanf("%lf",&F1);
printf("F2=");scanf("%lf",&F2);//这边格式输入一定要注意不能习惯于用%d,而应该用%lf!
if(n == 0) //定义初始值
return 0;
if(n == 1 )
return F1;
if(n == 2)
return F2;
int a=F1,b=F2,c=0; //定义初始值
//用一个for循环,a、b分别为前两项,c为前两项之和,得到c后进行交换更新a、b的值,进行n次交换即可。
for(int i=3;i<=n;i++) //更新操作
{
c = a+b;//从F(3)=F(1)+F(2)开始,相当于由上一步的结果得到F(n),这就叫迭代
a = b;//下一步的a=F(2)
b = c;//下一步的b=F(3)
}
return c; //c即为结果输出
}
int main()
{
//迭代法计算F(n)
printf("用迭代法计算斐波那契数列中的第%d项为:%d\n",n,Fibonacci_by_iteration(n));
return 0;实验结果:
下面我们紧接着就来谈“变态青蛙跳台阶”的问题:
问题描述:
一只青蛙可以一次跳 1 级台阶或一次跳 2 级台阶,兴奋的时候也可能跳三级台阶,例如:跳上第一级台阶只有一种跳法:直接跳 1 级即可。跳上两级台阶,有两种跳法: 每次跳 1 级,跳两次; 或者一次跳 2 级,跳第三级台阶共4种跳法,即“一级一级”+“跳一次三级”+“前二后一”+“前一后二”,问要跳上第 n 级台阶有多少种跳法?
先考察跳第一级台阶共几种跳法?很显然1种
(以下的“+”为加法原理的意思)
考察第二级台阶几种方法?
case1:跳一级到第一级台阶+跳1级到第二级台阶
case2:跳两级到第二级台阶
共2种方法
考察第三级台阶共几种方法?
case1:均跳1级
case2:前两级采用跳两级的方式+后一级跳一级
case3:第一级采用跳一级方式+后两级采用跳两级的方式
case4:一次三级
共4种方法
考察第四级台阶共几种方法?
case1:均跳一级
case2:跳两次两级
case3:第一次跳两级到第二级+第二次跳一次一级到第三级+第三次跳一次一级到第4级
case4:第一次跳一次一级到第一级+第二次跳一次二级到第三级+第三次跳一次一级到第4级
case5:第一次跳一次一级到第一级第二次跳一次一级到第二级+第三次跳一次二级到第4级
case6:前三后一
case7:前一后三
共7种跳法
...继续往下会发现变态青蛙跳台阶问题,第n级台阶共几种跳法=前三级台阶跳法之和,即满足初始值F[1]=1,F[2]=2,F[3]=4的递推关系式F[n]=F[n-1]+F[n-2]+F[n-3]。
那用迭代实现就是前文提到的:
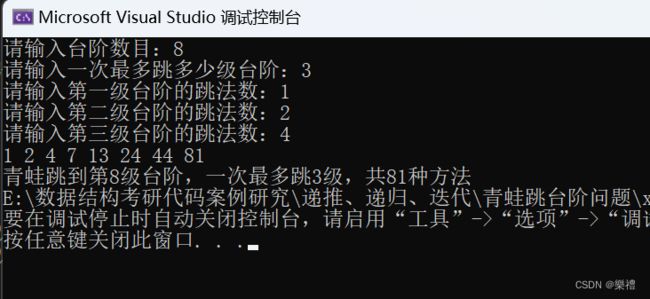
下面给出变态青蛙跳台阶问题的编程实现:
"algo_sum_pre_n.h":
#pragma once
void InitF_2(int F[], int& posf,int f1,int f2)//对满足F[n]=F[n-1]+F[n-2]数列的初值初始化
{
F[0] = f1;
F[1] = f2;
posf = 2;
}
void InitF_3(int F[], int& posf, int f1, int f2,int f3)//对满足F[n]=F[n-1]+F[n-2]+F[n-3]数列的初值初始化
{
F[0] = f1;
F[1] = f2;
F[2] = f3;
posf = 3;
}
//需求:迭代法计算F[i]位置前k项和
//迭代法计算F[i]位置前2项和
int sum_pre_2_by_iteration(int F[],int &posf,int a, int b,int n)
{
int c;
for (int i =3 ; i <=n; i++)//从第3级开始计算,一直计算到第n级,输出第n级的方法
{
c = a + b;
a = b;
b = c;
F[i-1]=c;
posf++;
}
return c;
}
//迭代法计算F[i]位置前3项和
int sum_pre_3_by_iteration(int F[],int &posf,int a,int b,int c,int n)
{
int d;
for (int i = 4; i <= n; i++)//从第4级开始计算,一直计算到第n级,输出第n级的方法
{
d = a + b + c;
a = b;
b = c;
c = d;
F[i - 1] = d;
posf++;
}
return d;
}main:
#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include "algo_sum_pre_n.h"
#define Maxsize 50
int main()
{
int n,k;
printf("请输入台阶数目:"); scanf("%d", &n);
printf("请输入一次最多跳多少级台阶:"); scanf("%d", &k);
int f1,f2,f3;
int num;
int F[Maxsize];//每个元素存放第i+1级台阶(数组从0开始,0号位置是第一级台阶的跳法数)总共的跳法数。
int posf = 0;
switch (k)
{
case 2:
printf("请输入第一级台阶的跳法数:"); scanf("%d", &f1);
printf("请输入第二级台阶的跳法数:"); scanf("%d", &f2);
InitF_2(F, posf, f1, f2);
num=sum_pre_2_by_iteration(F,posf,f1, f2, n);
for (int i = 0; i 测试结果:
依据上面的原理和迭代核心代码“更迭换代”的规律那么我们就可以写出“给定数列中任意k个项(4<=k
其归纳的思想为:
①申请一个变量k,存放前k项和
②第一轮循环k=初值和,而后执行各初值的“左移老化”操作(不清楚的看前面迭代的哲学原理部分),再在下一轮加上这一轮得到的k的值作为新鲜血液加入下一轮的操作。
三、递归的原理----以“求斐波那契数列第n项”的递归实现为例从递归调用栈来理解以及汉诺塔问题用递归实现的推导过程和可行性分析。
先来看一个所谓的无分支递归:
再来看一个在其他文章中给出求斐波那契数列第5项F[5]的所谓的有分支递归:
先给出我们熟悉的“求斐波那契数列第n项”的递归实现代码,而后给出以求F[5]为例在计算机内部产生的递归调用栈来说明递归的时候计算机都干了一些什么事:
//斐波那契递归实现
int Fibonacci_by_recursion(int n)
{
if(n == 1 || n == 2)
return 1;
return Fibonacci_by_recursion(n-1) + Fibonacci_by_recursion(n-2); //如果n != 1 && n != 2 进行递归运算
}
int main()
{
//递归计算F(n),特别慢
printf("用递归计算斐波那契数列中的第%d项为:%d\n",n,Fibonacci_by_recursion(n));
return 0;
}
注意看我用黄色记号笔标出来的红笔写的前置知识再根据从(I)到(V)再到⑥到F(5)出栈的顺序看计算机内部的递归调用栈是如何计算表达式F(4)+F(3)的,搞清楚什么时候把什么push进栈,什么条件可以return把什么pop出栈:
至此,在计算机内部根本就不存在什么“有分支递归”和“无分支递归”,所以我在上面加了“所谓的”,都是不懂数据结构和算法还有计算机基础知识的人观察现象得到的结论。计算机内部计算表达式只有“计算表达式的栈”,从表达式的左边开始依次push进栈,直到可以return这个元素的值的时候才从栈顶一层一层pop出栈,继续计算表达式下一个元素的值,直到可以return这个元素的值的时候才从栈顶一层一层pop出栈...
对于上述递归实现代码,返回的不就是表达式么,所以所有的递归实现代码都是这种结构:
“return 表达式”
而且递归实现中的表达式中的元素一定包括递归函数本身,只是传入的参数和上一层的递归传入的参数不一样罢了,这个表达式和所给的序列的递推关系一致。
//(我在写这篇文章
离散数学/组合数学:序列与其对应的生成函数;多项式函数的系数与序列的联系;重复组合数的理解方法即----全1序列对应的生成函数做n重卷积(不严谨说法)之后得到的序列的x的k次方项的系数;莫比乌斯反演。的时候,我发现,我为了完成这篇文章,作为一个大的工程项目(即可当作上文F(5)),按顺序列出提纲,从开始到结束的顺序,从①开始(即F(4))每次完成一个点再回过头来看下一个点②(即求F(4)时候紧接着想求F(3))再进去解决这个点的问题直到最后一个拆解的小问题解决完了(即上文到的F(1)和F(0))再来解决下一个点中的问题(即计算F(5)时要计算的F(3))直到这一个点的最后一个小问题解决了再回头来看下一点...直到解决可以标志某一个点解决的小点解决了就标志着这个模块的解决,所有的模块按顺序都解决了就表示递归结束,工程结束。这也是一个递归的过程,那么我们可以把递归的过程给出一个哲学的意义:
为解决一个庞大的工程项目,我们按照生活当中我们活着的时候能做的事的时间顺序(因为我们只能顺序的访问时间,我们不能跳跃的访问时间,我们对时间始终是1对1的顺序关系)先进行第一个子模块的处理,直到一个最小的问题的解决可以标志这个子模块的解决那么就可以回到子模块级别继续研究下一个子模块直到解决这个子模块解决的标志问题...最后所有的标志都解决了(return;栈空)那么就意味着整个项目的解决。)
所以我们就发现,递归代码对程序员来说写的代码结构是最简单的,但是从计算机的角度来说,它会形成一个递归调用栈,如果对于规模较大的递归,递归调用栈的层数过多又可能会造成内存泄漏,而且栈的层数一多,运算的速度就会大幅减慢,递归是效率非常低的算法。
那么理解了计算机内部求表达式的值的时候是用的递归调用栈之后,我们就了解了递归调用对计算机来说的本质,下面我们就来讨论一个经典的用递归实现的问题----“汉诺塔问题”,以及用递归实现它的推导过程和可行性分析。
问题描述:
汉诺塔(Tower of Hanoi),又称河内塔,是一个源于印度古老传说的益智玩具。大梵天创造世界的时候做了三根金刚石柱子,在一根柱子上从下往上按照大小顺序摞着64片黄金圆盘。大梵天命令婆罗门把圆盘从下面开始按大小顺序重新摆放在另一根柱子上。并且规定,在小圆盘上不能放大圆盘,在三根柱子之间一次只能移动一个圆盘。(源自百度百科)
数字特征:
我们设一个函数H(n)表示n个圆盘从A柱移动到C柱需要移动多少次
我们要先将(n-1)个圆盘从A移动到B柱,需要移动H(n-1)次
然后将1个圆盘从A移动到C柱,需要移动1次
再讲(n-1)个圆盘从B柱移动到C柱,需要移动H(n-1)次
因此H(n) = 2*H(n-1) +1,H(1)= 1;
我们就得到了递推公式
H(1) =1=2^1-1
H(2)=2(H(1))+1=2(2^1-1)+1=3=2^2-1
H(3)=2(H(2))+1=2(2^2-1)+1=7=2^3-1
H(4)=2(H(3))+1=2(2^3-1)+1=15=2^4-1
...
H(n)=2^n-1
可见:64个圆盘需要移动2^64-1次,假设1秒移动可以移动1次,差不多需要5845.42亿年以上。
移动过程推导:
代码实现:
#define _CRT_SECURE_NO_WARNINGS 1
#include
int count=0;//移动一次就记一次数,记录搬动圆盘的总次数
void Move(char from, char to) //移动剩余的一个圆盘的操作,将圆盘从源柱移动到目的柱
{
printf("将一个圆盘从%c柱 -> %c柱\n", from, to);
count++;//移动一次就记数就+1
}
void Hanoi(int n,char a, char b, char c) //总共有n个圆盘,将这n个圆盘 从 A柱 借助 B柱 移动到 C柱
{
if (n == 1) //当只有一个圆盘时,直接圆盘从 A 柱 移动到 C 柱
{
Move(a, c);
}
else
{
Hanoi(n-1,a, c, b); //当不只一个圆盘时,我们先将上面 (n -1)个圆盘看作整体 从 A 柱 借助 C柱 移动到 B 柱
Move(a, c); //A柱剩余一个圆盘,将剩下的一个圆盘从 A 移动到 C
Hanoi( n - 1,b, a, c); //再将(n-1)个圆盘从 B柱 借助 A柱 移动到 C柱
}
}
int main()
{
int n = 0; //汉诺塔层数
char a = 'A';//A柱
char b = 'B';//B柱
char c = 'C';//C柱
printf("请输入您初始化在汉诺塔A柱中的圆盘总数:");
scanf("%d", &n);
Hanoi(n,a, b, c);//将n个圆盘,借助于B柱子,从A柱子移动到C柱子
printf("圆盘一共移动%d次", count);
return 0;
}
测试结果:
至此,我们就理解了“递推、递归、迭代、差分方程”之间的关系,以及它们的实现原理和应用场景。
那么再回到之前讨论“给定数列中任意k个项(4<=k
核心是你首先得先制造出整个数列,你才能求这个数列第i个位置的前k项和,那我既然已经得到了整个数列,这个数列可能是公式实现的、迭代实现的、递归实现的,但是但凡要求区间和就一定是这个数列已经形成放到了某个数组arr中,而且还要求这个arr数组的前缀和数组sum!我再要求arr数列的第i项,你想通过求区间和的方法计算,然而,你忽略了,这个arr数组的每一项就是你制造出来的那个数列,你还要求什么区间和?你求的arr的区间和数列sum就肯定不是给的递推关系的那个数列了,你本应该直接循环输出,根本就用不上区间和。
以上就是近期研究的焦点问题一维数组范围内“数列的递推关系、通项公式实现、迭代实现、递归实现、一维数组的前缀和,区间和、差分数组、区间更新算法以及它们背后的数学原理”。
最后遗留的问题就是在实现差分方程求解的时候复数域的数学计算的问题,代码健壮性有待优化,有兴趣的朋友可以对我的代码提出优化意见。我会在我其他的文章中讨论复变函数的问题,这也是有关差分方程应用于信号过滤中的焦点问题。
特别鸣谢我远在南信大的好友岳华胜在差分方程求特征方程的常系数C1、C2时提供的宝贵参考意见!
如有问题欢迎随时与我沟通。