图论的基础
文章目录
- 基本概念
- 特性
- 无权图的描述
-
- 邻接矩阵
-
- 将邻接矩阵映射到数组
- 无向图的邻接矩阵/三角矩阵
- 邻接链表
- 邻接数组
- 加权图的描述
- 类的实现
-
- 邻接矩阵类
- 邻接链表类
- 图的遍历
-
- 广度优先搜索
- 深度优先
图的术语:顶点、边、邻接、关联、度、回路、路径、连通构建、生成树。
图的类型:无向图、有向图和加权图。
图的常用描述方式:邻接矩阵、矩阵邻接表和邻接链表。
图的标准搜索方法:广度优先搜索和深度优先搜索。
基本概念
图是一个用线或边连接在一起的顶点或节点的集合。
G = < V , E > G=
带方向的边称为有向边,反之称为无向边。
对于无向边,当且仅当 ( i , j ) (i,j) (i,j)是图的边,称顶点i和j是邻接的,边 ( i , j ) (i,j) (i,j)关联顶点i和j。
对于有向边,边 ( i , j ) (i,j) (i,j)关联至顶点j,关联于顶点i,顶点i邻接至j,顶点j邻接于i。
如果图的所有边都是无向边,那么该图称之为无向图;如果图的所有边都是有向边,那么该图称之为有向图。
一个图不能有重复的边,也不可能包含自连边/环。
我们为每条边赋予一个表示成本的值,称之为权,这时的图称之为加权有向图和加权无向图, G < V , E , W > G
在简单无向图中,如果V的每个结点都与其余所有节点邻接,我们称该图为无向完全图,记为 K n K_n Kn。同理,也可以如此定义有向完全图。
在有向图中,对任意节点 v ∈ V v\in V v∈V,以 v v v为始节点的弧的条数,称为节点 v v v的出度,记为 d + ( v ) d^+(v) d+(v);以 v v v为终节点的弧的条数,称为 v v v的入度,记为 d − ( v ) d^-(v) d−(v)。出度与入度之和称为节点的度数。
对于无向图,节点的度数等于连接它的边数。若v有环,则该点度因环而增加2。
给定无向图(或有向图) G = < V , E > G=
在一个图中,若 v i v_i vi到 v j v_j vj存在任何一条链/路,则称从 v i v_i vi到 v j v_j vj是可达的。为了完全起见,规定每个节点到自身都是可达的。
两个节点之间是可达的当前仅当它们属于同一个子图,称这种子图为图G的连通分图/分支,记连通分图的个数为 w ( G ) w(G) w(G)。如果图G只有一个连通分图,则称G是连通图;否则称G为非连通图或分离图。
特性
特性-1 设 G = ( V , E ) G=(V,E) G=(V,E)是一个无向图,令 n = ∣ V ∣ , e = ∣ E ∣ n=|V|,e=|E| n=∣V∣,e=∣E∣,则:1. ∑ i = 1 n d i = 2 e \sum_{i=1}^nd_i=2e ∑i=1ndi=2e; 2. 0 ≤ e ≤ n ( n − 1 ) 2 0\le e\le \frac{n(n-1)}{2} 0≤e≤2n(n−1)。
特性-2 设 G = ( V , E ) G=(V,E) G=(V,E)是一个有向图,令 n = ∣ V ∣ , e = ∣ E ∣ n=|V|,e=|E| n=∣V∣,e=∣E∣,则:1. 0 ≤ e ≤ n ( n − 1 ) 0\le e\le n(n-1) 0≤e≤n(n−1);2. ∑ i = 1 n d i + = ∑ i = 1 n d i − = e \sum_{i=1}^n d_i^+=\sum_{i=1}^n d_i^-=e ∑i=1ndi+=∑i=1ndi−=e
无权图的描述
邻接矩阵
一个n顶点的图 G = ( V , E ) G=(V,E) G=(V,E)的邻接矩阵是一个 n × n n\times n n×n的矩阵,其中的每个元素是0或者1.其中的元素定义如下:
A ( i , j ) = { 1 , i f ( i , j ) ∈ E o r ( j , i ) ∈ E 0 , o t h e r s A(i,j)=\left\{\begin{aligned}&1,if~(i,j)\in E~or~(j,i)\in E\\&0,~others\end{aligned}\right. A(i,j)={1,if (i,j)∈E or (j,i)∈E0, others
如果G是有向图,那么其中的元素定义如下:
A ( i , j ) = { 1 , i f ( i , j ) ∈ E 0 , o t h e r s A(i,j)=\left\{\begin{aligned}&1,if~(i,j)\in E\\&0,~others\end{aligned}\right. A(i,j)={1,if (i,j)∈E0, others
于是,我们可以得到如下性质:
- 对于n顶点的无向图,有 A ( i . i ) = 0 , 1 ≤ i ≤ n A(i.i)=0,1\le i\le n A(i.i)=0,1≤i≤n;
- 无向图的邻接矩阵是对称的,即 A ( i , j ) = A ( j , i ) , 1 ≤ i ≤ n , 1 ≤ j ≤ n A(i,j)=A(j,i),1\le i\le n,1\le j\le n A(i,j)=A(j,i),1≤i≤n,1≤j≤n;
- 对于n顶点的无向图,有 ∑ j = 1 n A ( i , j ) = ∑ j = 1 n A ( j , i ) = d i \sum_{j=1}^nA(i,j)=\sum_{j=1}^nA(j,i)=d_i ∑j=1nA(i,j)=∑j=1nA(j,i)=di;
- 对于n顶点的有向图,有 ∑ j = 1 n A ( i , j ) = d i + , ∑ j = 1 n A ( j , i ) = d i − \sum_{j=1}^nA(i,j)=d_i^+,\sum_{j=1}^nA(j,i)=d_i^- ∑j=1nA(i,j)=di+,∑j=1nA(j,i)=di−
将邻接矩阵映射到数组
- 映射到 ( n + 1 ) × ( n + 1 ) (n+1)\times (n+1) (n+1)×(n+1)大小的布尔数组,这保证了索引与序号的对应关系;
- 映射到 n × n n\times n n×n大小的布尔数组,这可以节省一定的空间;
- 映射到 ( n − 1 ) × n (n-1)\times n (n−1)×n大小的布尔数组,这是因为对角线元素可以直接省略。
对这三种情况进行考量,可以发现,其实2、3两种方法节省的不是很多,而且操作起来还很麻烦。建议还是第一种。
无向图的邻接矩阵/三角矩阵
对于特别的无向图的邻接矩阵而言,因为是对称的,所以可以用三角矩阵的表示方法,用一个大小为 n ( n + 1 ) 2 \frac{n(n+1)}{2} 2n(n+1)的一维数组表示。
考察一个下三角矩阵,如果 i < j i\lt j i<j,那么 L ( i , j ) = 0 L(i,j)=0 L(i,j)=0;如果 i ≥ j i\ge j i≥j,则 L ( i , j ) L(i,j) L(i,j)位于非0区域。
template<class T>
void lowerTriangularMatrix<T>::set(int i, int j, const T&newValue){
// 检验i,j是否合法
if(i<1 || j<1 || i>n || j>n)
throw matrixIndexOutOfBounds();
if(i>=j)
element[i*(i-1)/2+j-1] = newValue;
else
if(newValue !=0){
throw illegalParameterValue
}
}
其中,重点是下三角矩阵到一维数组的映射。
理解:在元素 L ( i , j ) ( i ≥ j ) L(i,j)(i\ge j) L(i,j)(i≥j)之前分别有 ∑ k = 1 i − 1 k \sum_{k=1}^{i-1}k ∑k=1i−1k个元素位于第1行至第i-1行的非0区域以及j-1个元素位于第i行的非0区域,即共有 i ( i − 1 ) / 2 + j − 1 i(i-1)/2+j-1 i(i−1)/2+j−1。这也是一维数组的索引。即表示的是下三角矩阵中,L(i,j)是第几个数。
使用邻接矩阵时,确定邻接至或邻接于一个给定节点的集合,需要用时 Θ ( n ) \Theta(n) Θ(n)。然而,增加或删除一条边只要 Θ ( 1 ) \Theta(1) Θ(1).
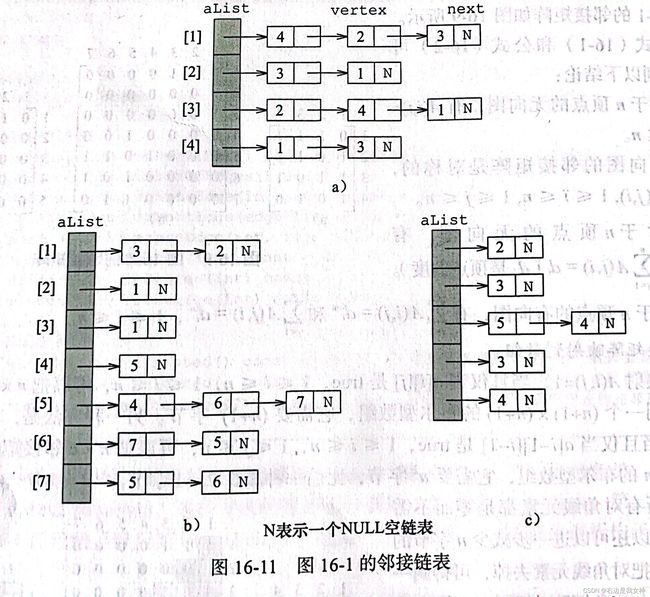
邻接链表
一个顶点i的邻接表是一个线性表,它包含所有 邻接于顶点i的顶点。
图的每个顶点都有一个邻接表。当邻接表用链表表示时,就是邻接链表(linked-adjacency-list)。
当e远远小于 n 2 n^2 n2时,邻接链表比邻接矩阵需要更少的空间。
在邻接链表中,确定邻接于顶点i的顶点需要用时 Θ ( 邻 接 于 顶 点 i 的 顶 点 数 ) \Theta(邻接于顶点i的顶点数) Θ(邻接于顶点i的顶点数),插入或删除一条边(i,j)的用时,对无向图来说是 O ( d i + d j ) O(d_i+d_j) O(di+dj),对有向图是 O ( d i + ) O(d_i^+) O(di+)。
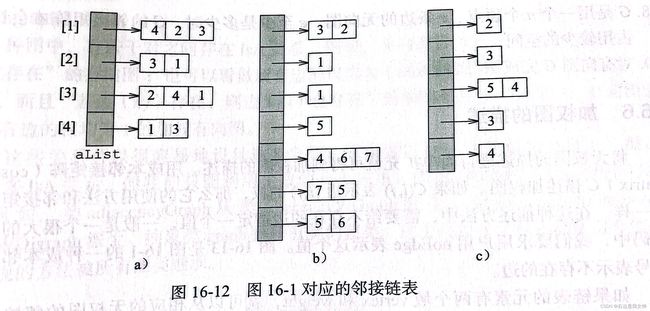
邻接数组
在邻接数组中,每一个邻接表用一个数组线性表而非链表来描述。
邻接数组比邻接链表少用4m字节,因为不需要next指针域。理论上来说,两者的时间复杂度是相通的。但实验表明,大部分的图操作,邻接数组的用时要少于邻接链表。
加权图的描述
将无权图的描述进行简单的扩充就可以得到加权图的描述。
成本邻接矩阵C描述加权图。 C ( i , j ) C(i,j) C(i,j)表示边 ( i , j ) (i,j) (i,j)的权。给不存在的边通常指定一个很大的值。
对于邻接链表而言,只要将每一个node增加一个weight域就可以了。
对于邻接数组而言,只要将每一个element改成pair就行了。
类的实现
一共有四种图:无权无向图、无权有向图、加权无向图、加权有向图。
每种图有三种实现方式,分别是邻接矩阵、邻接链表和邻接数组。
邻接矩阵类
template <class T>
class adjacencyWDigraph{
protected:
int n; // 顶点个数
int e; // 边的个数
T **a; // 邻接数组
T noEdge; // 表示不存在的边
public:
adjacencyWDigraph(int numberOfVertices = 0, T theNoEdge = 0){
if(numberOfVertices<0)
throw illegalParameterValue;
n = numberOfVertices;
e = 0;
noEdge = theNoEdge;
make2Array(a,n+1,n+1);
for(int i=1; i<=n; i++)
// 初始化邻接矩阵
fill(a[i],a[i]+n+1,noEdge); // 所有的元素初始化为noEdge
}
~adjacencyWDigraph(){delete2dArray(a,n+1);}
int numberOfVertices() const {return n;} // 返回节点的数量
int numberOfEdges() const {return e;} // 返回边的数量
bool directed() const {return true;} // 是否是有向图
bool weighted() const {return true;} // 是否是加权图
bool existsEdge(int i, int j) const // 是否存在边
if(i<1 || j<1 || i>n || j>n || a[i][j] == noEdge)
return false;
else
return true
void insertEdge(edge<T> *theEdge){
// 插入边,如果边已经存在,则用theEdge->weight() 修改边的权
int v1 = theEdge->vertex1();
int v2 = theEdge->vertex2();
if (v1<1 || v2<1 || v1>n || v2>n || v1==v2){
throw eillegalParameterValue(s.str());
}
if(a[v1][v2]==noEdge) // 新的边
e++;
a[v1][v2] = theEdge->weight();
}
void eraseEdge(int i,int j){
// 删除边
if(i>=1&&j>=1&&i<=n&&j<=n&&a[i][j]!=noEdge){
a[i][j] = noEdge;
e--;
}
}
}
邻接链表类
class linkedDigraph{
protected:
int n; // 顶点数
int e; // 边数
graphChain<int> *aList // 邻接表
public:
linkedDigraph(int numberOfVertices = 0){
// 构造函数
if(numberOfVertices<0)
throw illegalParameterValue;
n = numberOfVertices;
e = 0;
aList = new graphChain<int>[n+1];
}
~linkedDigraph() {delete [] aList;}
...(numberOfVertices/numberOfEdges/directed/weighted)
bool existsEdge(int i, int j) const // 是否存在边
if(i<1 || j<1 || i>n || j>n || aList[i].indexOf(j) == -1)
return false;
else
return true
void insertEdge(edge<bool> *theEdge){
// 插入一条新边
// 检验边的有效性,此处不再赘述
if(aList[v1].indexOf(v2) == -1){
aList[v1].insert(0,v2);
e++;
}
}
void eraseEdge(int i, int j){
if(i>=1&&j>=1&&i<=n&&j<=n){
if *v = aList[i].eraseElement(j);
if(v!=NULL) // 边(i,j)存在
e--;
}
}
}
图的遍历
广度优先搜索
设G是一个任意类型的图,v是G的任意一个顶点,下述代码能够标记从v出发可以到达的所有顶点。
breadthFirstSearch(v){
1: 设定起始节点v;
2: 初始化队列Q,并将v放入其中;
3: while(Q非空){
4: 从队列中取出节点w;
5: 记w的一个邻接点为u;
6: while(u!=NULL){
7: if(u没有被标记过){
8: 将u加入到队列中;
9: 标记u;
10: }
11: 令u成为w的下一个邻接点。
12: }
13: }
}
深度优先
depthFirstSearch(v){
1: 标记v未已经到达;
2: for(对每一个与v邻接的u)
3: depthFirstSearch(u);
}