代码随想录算法训练营第三十五天| 贪心算法 part04

860. 柠檬水找零

在柠檬水摊上，每一杯柠檬水的售价为 5 美元。顾客排队购买你的产品，（按账单 bills 支付的顺序）一次购买一杯。

每位顾客只买一杯柠檬水，然后向你付 5 美元、10 美元或 20 美元。你必须给每个顾客正确找零，也就是说净交易是每位顾客向你支付 5 美元。

注意，一开始你手头没有任何零钱。

给你一个整数数组 bills ，其中 bills[i] 是第 i 位顾客付的账。如果你能给每位顾客正确找零，返回 true ，否则返回 false 。

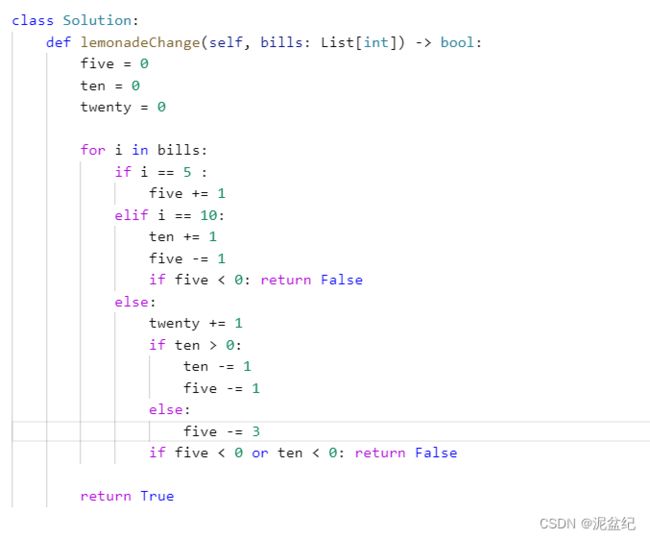
这题我完全没用贪心算法，直接判断各种可能的情况就行了， 如果最后 5元和10元的计数器小于0了就是找不出来：

 贪心算法，看上去复杂，其实逻辑都是固定的！LeetCode：860.柠檬水找零_哔哩哔哩_bilibili

406. 根据身高重建队列

假设有打乱顺序的一群人站成一个队列，数组 people 表示队列中一些人的属性（不一定按顺序）。每个 people[i] = [hi, ki] 表示第 i 个人的身高为 hi ，前面 正好 有 ki 个身高大于或等于 hi 的人。

请你重新构造并返回输入数组 people 所表示的队列。返回的队列应该格式化为数组 queue ，其中 queue[j] = [hj, kj] 是队列中第 j 个人的属性（queue[0] 是排在队列前面的人）。

这题真的没有头绪，先去学习：

贪心算法，不要两边一起贪，会顾此失彼 | LeetCode：406.根据身高重建队列_哔哩哔哩_bilibili

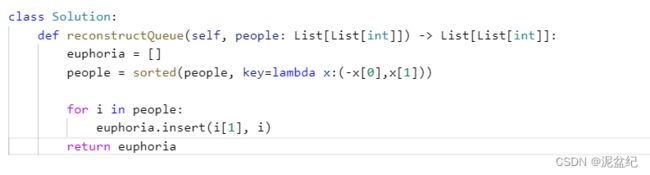
这道题确定先排序哪个维度挺重要，顺便复习了python的匿名函数和insert函数

Python的insert()函数用于将指定对象插入列表的指定位置。插入操作会改变列表的长度，原位置及之后的元素都会向后移动一个位置。这个函数有两个参数，第一个参数是要插入的位置的索引值，第二个参数是要插入的对象。

举个例子来说明，如果有一个列表lst = [2, 4, 6, 8]，我们可以使用lst.insert(1, 3)来在索引位置1处插入数字3，结果就成为了[2, 3, 4, 6, 8]。在这个例子中，数字3被插入到了索引位置1处，原来的元素都向后移动一个位置。

需要注意的是，如果指定的位置超出了列表的长度，插入操作会将元素插入到列表的末尾。比如，如果我们使用lst.insert(10, 9)，在索引位置10处插入数字9，由于列表lst的长度为4，所以数字9会被插入到列表的末尾，结果就成为了[2, 4, 6, 8, 9]。

另外，如果插入的位置是负数，它会从列表的末尾开始计算。比如，如果我们使用lst.insert(-1, 7)，在倒数第二个位置插入数字7，结果就成为了[2, 4, 6, 7, 8]。在这个例子中，数字7被插入到了倒数第二个位置，原来的元素都向后移动一个位置。

总结一下，Python的insert()函数可以在列表的指定位置插入一个对象，如果插入的位置超出了列表的长度，对象会被插入到列表的末尾。如果插入的位置是负数，它会从列表的末尾开始计算。

首先按照身高排序,身高一定是从大到小排（身高相同的话则k小的站前面），让高个子在前面。

然后再按照k来插入对应的位置。

452. 用最少数量的箭引爆气球

有一些球形气球贴在一堵用 XY 平面表示的墙面上。墙面上的气球记录在整数数组 points ，其中points[i] = [xstart, xend] 表示水平直径在 xstart 和 xend之间的气球。你不知道气球的确切 y 坐标。

一支弓箭可以沿着 x 轴从不同点 完全垂直 地射出。在坐标 x 处射出一支箭，若有一个气球的直径的开始和结束坐标为 xstart，xend， 且满足  xstart ≤ x ≤ xend，则该气球会被 引爆 。可以射出的弓箭的数量 没有限制 。 弓箭一旦被射出之后，可以无限地前进。

给你一个数组 points ，返回引爆所有气球所必须射出的 最小 弓箭数 。

贪心算法，判断重叠区间问题 | LeetCode：452.用最少数量的箭引爆气球_哔哩哔哩_bilibili

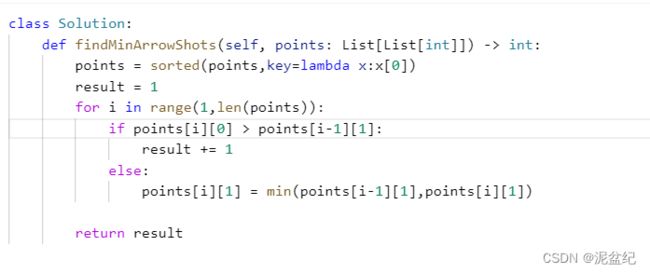
这道题代码看上去简单，但是细节非常之多：

1 记录次数的result数组初始化数组应该是1，因为如果气球不为空最少需要一根箭来射气球。

2 先将数组按照左边界即points[i][0]从小到大排好序来确定边界

3 然后就是判断气球的重叠问题，如果只有两个气球，只需判断右边界是否小于之前气球的左边界即可。

4 难点在于 如果要三个或三个以上的气球是否重合呢？ 做法是更新当前气球的右边界，更新后的值应该取最小值 min(points[i-1][1], points[i][1])，如果不满足这个要求，那就需要加一枝箭了。