【代码分析】cublasSgemm 矩阵乘法详解
目录
前言
预备知识
cublasSgemm 函数
求解C=AxB
不使用cublasSgemm transa与transb参数
示例程序
使用cublasSgemm transa与transb参数
示例程序
前言
cublasSgemm是NV cublas库的矩阵相乘API，由于cublas中矩阵的存储是列优先，所以cublasSgemm API的参数让新手一头雾水，经过仔细研究和实践后总结为本文，便于后来者参考
预备知识
行优先还是列优先
矩阵存储示意
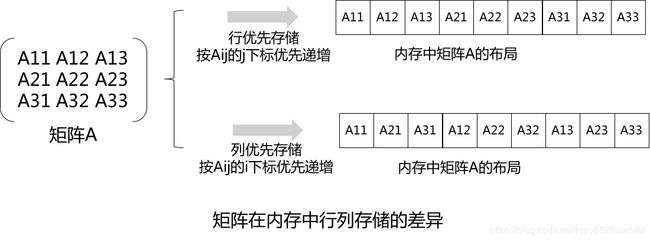
矩阵在逻辑上表达为2维M行K列，但存储到内存的时候都是按一维布局，其中按行优先存储和按列优先存储的差异如上图所示
行优先存储到列优先读取对矩阵的变化影响
如上图所示，当矩阵按行优先存储然后又按相反的列优先读取的话，就会得到元矩阵转置的结果；同理适用于按列优先存储然后按行优先读取。
cublasSgemm 函数
cublasStatus_t cublasSgemm(cublasHandle_t handle,
cublasOperation_t transa, cublasOperation_t transb,
int m, int n, int k,
const float *alpha,
const float *A, int lda,
const float *B, int ldb,
const float *beta,
float *C, int ldc)
cublasSgemm的官方API说明文档链接 https://docs.nvidia.com/cuda/cublas/index.html
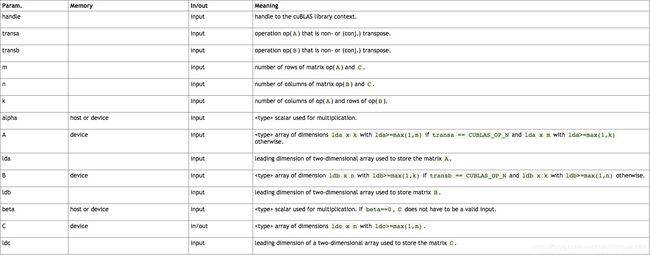
- 根据文档说可以知道，cublasSgemm完成了 C = alpha * op ( A ) * op ( B ) + beta * C 的矩阵乘加运算
- 其中alpha和beta是标量， A B C是以列优先存储的矩阵
- 如果 transa的参数是CUBLAS_OP_N 则op(A) = A ，如果是CUBLAS_OP_T 则op(A)=A的转置
- 如果 transb的参数是CUBLAS_OP_N 则op(B) = B ，如果是CUBLAS_OP_T 则op(B)=B的转置
由于API中的矩阵参数也用A B C表示，为了不和下面例子中的矩阵A B混淆，我们将cublasSgemm中的参数做如下的调整
- A称为乘法左矩阵
- B称为乘法右矩阵
- C称为结果矩阵
所以当alpha =1 并且 beta =0 的时候 cublasSgemm完成了计算： 结果矩阵= op (乘法左矩阵) * op ( 乘法右矩阵)
求解C=AxB
其中(A为M行K列 B为K行N列 所以 C为M行N列）
不使用cublasSgemm transa与transb参数
由于C/C++程序中输入的A和B是按行存储，所以在的情况下，cublas其实读取到的是A和B的转置矩阵AT和BT
根据线性代数的规则可知CT = (A x B)T = BT x AT 所以cublasSgemm API中几个参数设置如下
- 设置了cublasSgemm的transa与transb参数=CUBLAS_OP_N
- 乘法左矩阵为BT=参数设置为B，乘法右矩阵为AT=参数设置为A
- 结果矩阵的行数为CT的行数=参数设置为N
- 结果矩阵的列数为CT的列数=参数设置为M
- 乘法左矩阵列与乘法右矩阵的行=参数设置为K
- 按列优先读取乘法左矩阵B的主维度（即BT有几行）=参数设置为N
- 按列优先读取乘法右矩阵A的主维度（即AT有几行）=参数设置为K
- 结果矩阵存储在参数C中，它的主维度（即有几行）= 参数设置为N
cublasSgemm(handle,CUBLAS_OP_N,CUBLAS_OP_N, N, M, K,&alpha,d_b, N, d_a, K,&beta, d_c, N)
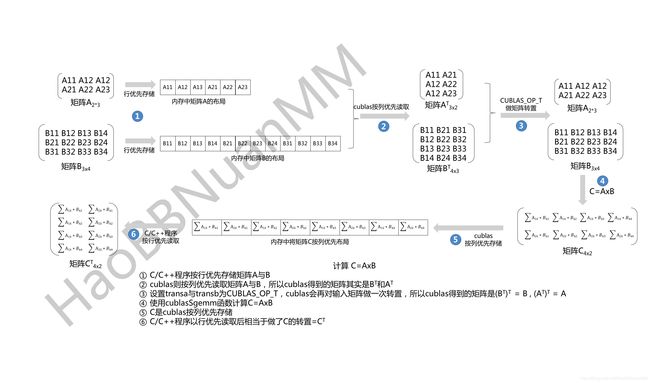
按上面的参数调用cublasSgemm API (矩阵A按行存储在指针d_a, 矩阵B按行存储在指针d_b, 矩阵C的存储空间指针d_c) 最后从结果矩阵的存储空间d_c中按行读取到的就是C=AxB的结果，整个cublasSgemm的计算过程如下图所示
不使用transa与transb参数的情况下 cublasSgemm 求解矩阵乘法的过程
示例程序
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define M 2
#define N 4
#define K 3
void printMatrix(float (*matrix)[N], int row, int col) {
for(int i=0;i 输入 A = 
B = 
运行结果 C = AxB = 
示例程序的cublasSgemm计算求解过程
使用cublasSgemm transa与transb参数
由于C/C++程序中输入的A和B是按行存储，所以在的情况下，cublas其实读取到的是A和B的转置矩阵AT和BT
设置了cublasSgemm的transa与transb参数后可以在做矩阵运算前对读取到的AT和BT矩阵做一次转置，获得A和B
根据线性代数的规则可知C = A x B 所以cublasSgemm API中几个参数设置如下
- 设置了cublasSgemm的transa与transb参数=CUBLAS_OP_T，在进行矩阵运算前对读取的矩阵做一次转置
- 乘法左矩阵为A=参数设置为A，乘法右矩阵为B=参数设置为B
- 结果矩阵的行数为C的行数=参数设置为M
- 结果矩阵的列数为C的列数=参数设置为N
- 乘法左矩阵列与乘法右矩阵的行=参数设置为K
- 按列优先读取乘法左矩阵A的主维度（即AT有几行）=参数设置为K
- 按列优先读取乘法右矩阵B的主维度（即BT有几行）=参数设置为N
- 结果矩阵存储在参数C中，它的主维度（即有几行）= 参数设置为M
cublasSgemm(handle,CUBLAS_OP_T,CUBLAS_OP_T, M, N, K,&alpha,d_a, K, d_b, N,&beta, d_c, M);
红色的参数标记出与“不使用cublasSgemm transa与transb参数”例子中的不同，按上面的参数调用cublasSgemm API (矩阵A按行存储在指针d_a, 矩阵B按行存储在指针d_b, 矩阵C的存储空间指针d_c) 最后从结果矩阵的存储空间d_c中按行读取到的就是C=AxB后CT的结果，所以在C/C++程序中还需要对读取的结果CT做一次矩阵转置操作才能获得最终正确的C。整个cublasSgemm的计算过程如下图所示
使用transa与transb参数的情况下 cublasSgemm 求解矩阵乘法的过程
示例程序
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define M 2
#define N 4
#define K 3
void printMatrix2(float* matrix, int row, int col) {
for(int i=0;i 输入 A = B =
运行结果由于按行优先N行M列的顺序读取h_C相当于做了C的转置，得到CT = 
在学习cublasSgemm API访问计算结果C的二维矩阵过程中，重新复习了一下二维矩阵的指针访问，可以参考我的另外一篇博文 【程序分析】指针与二维数组的访问