二叉树的遍历 (Java 深度前中后序遍历,广度层次遍历)
二叉树的定义,只要给定当前节点数据,左右节点即可.
/**
* @author Relic
* @desc 二叉树
* @date 2019-12-10 16:56
*/
@Data
public class BinaryTreeNode {
/**
* 当前节点的数据
*/
private E data;
/**
* 二叉树左节点
*/
private BinaryTreeNode leftChild;
/**
* 二叉树右节点
*/
private BinaryTreeNode rightChild;
public BinaryTreeNode(E e) {
this.data = e;
}
}
二叉树的遍历分为广度遍历还有深度遍历
广度里面又可以分为前序,中序,后序遍历.前序遍历
为了展示遍历结果,我写了一个生成树的方法,还有打印当前生成树的方法,定义了一个类负责实现不同的遍历方式.
/**
* 生成树的方法
*
* @return 生成的树的根节点
*/
private BinaryTreeNode generateTree() {
BinaryTreeNode root = new BinaryTreeNode<>(1);
BinaryTreeNode left = new BinaryTreeNode<>(2);
BinaryTreeNode right = new BinaryTreeNode<>(3);
root.setLeftChild(left);
root.setRightChild(right);
left.setLeftChild(new BinaryTreeNode<>(4));
left.setRightChild(new BinaryTreeNode<>(5));
right.setLeftChild(new BinaryTreeNode<>(6));
right.setRightChild(new BinaryTreeNode<>(7));
return root;
}
/**
* 画一下设置好的树,方便理解
*/
private void drawTree() {
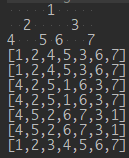
System.out.println(" 1 ");
System.out.println(" 2 3 ");
System.out.println("4 5 6 7");
} /**
* 抽象类,用于自定义遍历方法,并打印结果
*/
abstract class BaseTravelMethod {
protected static StringJoiner SJ = new StringJoiner(",", "[", "]");
/**
* 遍历节点
*
* @param root 根节点
*/
protected abstract void travel(BinaryTreeNode root);
public void print(BinaryTreeNode root) {
travel(root);
System.out.println(SJ.toString());
SJ = new StringJoiner(",", "[", "]");
}
} 深度遍历
前序遍历
前序遍历每个节点都是在子树遍历前进行处理的,也就是我先处理当前节点,然后再处理左右子节点.虽然先处理了当前的数据,但是还是要保存当前节点的数据,因为遍历完左子节点,还需要原节点才能取到右子节点,很明显是是后进先出的结构( LIFO ).那么可以得出,需要使用到栈这种数据结构.
递归实现
递归其实也是使用了栈,但这个栈由系统来维护.不需要我们去显示维护.
private BaseTravelMethod getPreOrderTravel() {
return new BaseTravelMethod() {
/**
* 递归前序遍历
*
* @param root 根节点
*/
@Override
protected void travel(BinaryTreeNode root) {
if (root != null) {
SJ.add(root.getData().toString());
travel(root.getLeftChild());
travel(root.getRightChild());
}
}
};
} 非递归实现
首先,我们将根节点压入自己定义好的栈中,同时处理该节点,然后将当前节点赋值为他的左子节点,重复该操作直到叶子节点.然后弹出叶子节点,将下次重新进入循环的节点置为右子节点,重新开始循环.直到栈空( 根节点也被弹出 )
private BaseTravelMethod getPreOrderNoRecursionTravel() {
return new BaseTravelMethod() {
/**
* 前序遍历(借助栈)
* 1.一直压栈直到寻找到最左边的叶子节点(压栈的同时输出当前节点)
* 2.弹出最左边的叶子节点,此时栈顶元素为叶子节点的父节点,将下次要遍历的节点转为该节点的右节点
* 3.重复循环
*
* @param root 根节点
*/
@Override
protected void travel(BinaryTreeNode root) {
ArrayStack> stack = new ArrayStack<>();
while (true) {
while (root != null) {
SJ.add(root.getData().toString());
stack.push(root);
root = root.getLeftChild();
}
if (stack.empty()) {
break;
}
root = stack.pop();
root = root.getRightChild();
}
}
};
} 中序遍历
中序遍历和前序遍历类似,他是先访问左节点,然后自身,然后是右节点.递归的写法最为简单.
递归实现
private BaseTravelMethod getMiddleOrderTravel() {
return new BaseTravelMethod() {
/**
* 递归中序遍历
*
* @param root 根节点
*/
@Override
protected void travel(BinaryTreeNode root) {
if (root != null) {
travel(root.getLeftChild());
SJ.add(root.getData().toString());
travel(root.getRightChild());
}
}
};
}
非递归实现
与前序非递归实现差不多,但是我们处理数据是在压入所有左子节点之后进行的.可以对比前后代码看下.
private BaseTravelMethod getMiddleOrderNoRecursionTravel() {
return new BaseTravelMethod() {
/**
* 非递归中序遍历
*
* @param root 根节点
*/
@Override
protected void travel(BinaryTreeNode root) {
ArrayStack> stack = new ArrayStack<>();
while (true) {
while (root != null) {
stack.push(root);
root = root.getLeftChild();
}
if (stack.empty()) {
break;
}
root = stack.pop();
SJ.add(root.getData().toString());
root = root.getRightChild();
}
}
};
} 后序遍历
递归实现
递归实现依旧如常的简单
private BaseTravelMethod getPostOrderTravel() {
return new BaseTravelMethod() {
/**
* 递归后序遍历
*
* @param root 根节点
*/
@Override
protected void travel(BinaryTreeNode root) {
if (root != null) {
travel(root.getLeftChild());
travel(root.getRightChild());
SJ.add(root.getData().toString());
}
}
};
}
非递归实现
最难的来了...
因为前序和中序遍历中,元素出栈后不需要再访问了,而后序遍历是先遍历左右子节点然后才处理当前节点,难题就是我们怎么判断当前节点的出栈时机呢.
解决方法是:判断弹出的元素是否是弹出后的栈顶元素的右子节点,如果是的话,说明已经遍历过左子节点了,而且右子节点也在刚刚遍历结束.
那么就是代码实现
private BaseTravelMethod getPostOrderNoRecursionTravel() {
return new BaseTravelMethod() {
/**
* 非递归后序遍历
*
* @param root 根节点
*/
@Override
protected void travel(BinaryTreeNode root) {
ArrayStack> stack = new ArrayStack<>();
while (true) {
if (root != null) {
stack.push(root);
root = root.getLeftChild();
} else {
if (stack.empty()) {
break;
} else if (stack.peek().getRightChild() == null) {
SJ.add(stack.peek().getData().toString());
//判断当前出栈的节点是出栈后栈顶的右子节点则说明子节点遍历结束 (虽然逻辑可能不会进去,但是 pop 每次都是会进行的)
while (stack.pop() == stack.peek().getRightChild()) {
//当栈的容量只剩 1 的时候,不要再去尝试遍历了( pop 之后 栈空,尝试 peek 抛出异常),此时只剩根节点了 直接处理
if (stack.size() == 1) {
SJ.add(stack.pop().getData().toString());
break;
}
SJ.add(stack.peek().getData().toString());
}
}
if (!stack.empty()) {
root = stack.peek().getRightChild();
} else {
root = null;
}
}
}
}
};
} 广度遍历
层次遍历
处理当前一层,然后深度 depth + 1,继续处理下一层,可以看出他的顺序是:先进先出( FIFO ),此处就要使用队列来进行辅助实现.
1.入队根节点,然后以队列不为空作为条件开始遍历.
2.出队,处理出队的节点,入队出队节点的非空左右子节点.
3.直到循环结束
private BaseTravelMethod getLevelOrderTravel() {
return new BaseTravelMethod() {
/**
* 层次遍历 (利用队列)
*
* @param root 根节点
*/
@Override
protected void travel(BinaryTreeNode root) {
DynamicArrayQueue> queue = new DynamicArrayQueue<>();
queue.enQueue(root);
while (!queue.isEmpty()) {
BinaryTreeNode father = queue.deQueue();
SJ.add(father.getData().toString());
BinaryTreeNode leftChild = father.getLeftChild();
BinaryTreeNode rightChild = father.getRightChild();
if (leftChild != null) {
queue.enQueue(leftChild);
}
if (rightChild != null) {
queue.enQueue(rightChild);
}
}
}
};
} 那么就是测试方法,还有结果啦.
@Test
public void binaryTree() {
drawTree();
BinaryTreeNode root = generateTree();
getPreOrderTravel().print(root);
getPreOrderNoRecursionTravel().print(root);
getMiddleOrderTravel().print(root);
getMiddleOrderNoRecursionTravel().print(root);
getPostOrderTravel().print(root);
getPostOrderNoRecursionTravel().print(root);
getLevelOrderTravel().print(root);
}
所以大致是知道dfs使用栈,bfs使用队列.
文中代码用的自定义栈和队列都在前面的文章有讲到,并且有实际代码,复制即可运行.