poj 1753 Flip Game (高斯消元 + 枚举 自由变量)

http://poj.org/problem?id=1753

题意：

有4*4的正方形，每个格子要么是黑色，要么是白色，当把一个格子的颜色改变(黑->白或者白->黑)时，其周围上下左右(如果存在的话)的格子的颜色也被反转，问至少反转几个格子可以使4*4的正方形变为纯白或者纯黑？

 这道题 可以 用 bfs  也可用 dfs 但在学 Gauss 就用了 Gauss，费劲 ，还有枚举 自由变量的所有可能 ，好，麻烦（

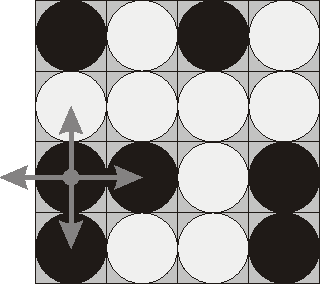
因为 自由变量的值可以影响 确定的 变量的值 所以 要 枚举所有的可能 来确定最小值

）。。。。。。

  1 #include<cstdio>
  2 #include<cstring>
  3 #include<cmath>
  4 #include<iostream>
  5 #include<algorithm>
  6 #include< set>
  7 #include<map>
  8 #include<queue>
  9 #include<vector>
 10 #include< string>
 11  #define Min(a,b) a<b?a:b
 12  #define Max(a,b) a>b?a:b
 13  #define CL(a,num) memset(a,num,sizeof(a));
 14  #define maxn  300
 15  #define eps  1e-12
 16  #define inf 100000000
 17  #define mx 1<<60
 18  #define ll   __int64
 19  const  double pi  = acos(- 1.0);
 20  using  namespace std;
 21  int  n =  4;
 22  int find( int i, int j)
 23 {
 24      return  i*n + j ;
 25 }
 26  int a[maxn][maxn] ;
 27  int free_x[maxn] ;
 28  int x[maxn];
 29  void init()
 30 {
 31     CL(a, 0);
 32      int i,j,y;
 33 
 34      for(i =  0 ;i < n;i++)
 35     {
 36          for(j =  0;j< n;j++)
 37         {
 38              int x = find(i,j);
 39             a[x][x] =  1;
 40              if(i -  1>= 0)
 41             {
 42                 y = find(i -  1,j);
 43                 a[x][y] =  1;
 44             }
 45              if(j +  1< n)
 46             {
 47                 y = find(i,j + 1);
 48                 a[x][y] =  1;
 49             }
 50              if(i +  1 < n)
 51             {
 52                  y = find(i +  1,j);
 53                  a[x][y] =  1;
 54 
 55             }
 56              if(j -  1 >= 0)
 57             {
 58                 y = find(i,j -  1);
 59                 a[x][y] =  1;
 60             }
 61         }
 62     }
 63 }
 64  int gcd( int x, int y)
 65 {
 66      int t ;
 67      while(y)
 68     {
 69         t = y;
 70         y = x%y;
 71         x = t;
 72     }
 73      return  x;
 74 }
 75  int lcm(  int x, int y)
 76 {
 77      return (x*y)/gcd(x,y);
 78 }
 79  int Gauss( int  var, int equ)
 80 {
 81      int  i,j,free_index;
 82      int max_r,k,col;
 83      int LCM,tmp;
 84      int free_num;
 85      int num =  0;
 86      for(i = 0  ; i<= var;i++)
 87     {
 88         free_x[i] =  0;  //  记录自由变元的
 89          x[i] =  0 ;
 90     }
 91      for(k =  0 ,col =  0;k<equ&&col< var;k++,col++)
 92     {
 93         max_r= k;
 94          for(i = k+ 1;i<equ;i++)
 95         {
 96              if(abs(a[i][col]) > abs(a[max_r][col]))max_r = i;
 97         }
 98          if(a[max_r][col] ==  0)
 99         {
100             k--;
101             free_x[num++] = col;
102              continue ;
103         }
104          if(max_r!=k)
105         {
106              for(i =  0;i <  var+ 1;i++)
107             {
108                 swap(a[k][i],a[max_r][i]);
109             }
110         }
111          for(i = k +  1;i<equ;i++)
112         {
113              if(a[i][col] != 0)
114             {
115                  // LCM = lcm(abs(a[k][col]),abs(a[i][col]));
116                   // int ta = LCM/a[i][col],tb = LCM/a[k][col] ;
117                   // if(a[i][col]*a[k][col] < 0) tb = - tb;
118                   for(j = col;j< var +  1;j++)
119                 {
120                     a[i][j] = a[i][j]^a[k][j];
121                 }
122             }
123         }
124     }
125 
126      for(i = k;i < equ;i++)
127     {
128          if(a[i][col] !=  0)   return - 1;
129     }
130      int ans =  0 ;
131      int stat =  1<<( var - k)  ; // 自由变元 有 var - k 个
132       int res = inf ;
133     //  因为 自由变量的值可以影响 确定的变量的值 所以 要 枚举所有的可能 来确定最小值
134       for(i =  0 ; i < stat;i++) // 枚举所有的 自由变量的状态
135      {
136         int   cnt =  0;
137         int  index = i;
138          for(j =  0;j <  var - k ;j++) // 对 ，对应的自由变量 赋值
139          {
140             x[free_x[j]] = (index& 1);
141 
142              if(x[free_x[j]])cnt++;
143             index>>= 1;
144         }
145 
146          for(j = k -  1 ; j >= 0;j--) // 带回 已经确定的变量，看是否 自由变量的 改变 影响 了其的值
147          {
148              int tmp = a[j][ var];
149              for( int  l = j +  1;l< var;l++)
150             {
151                
152                  if(a[j][l])tmp^=x[l] ;
153             }
154             x[j] = tmp ;
155              if(x[j])cnt++;
156         }
157          if( cnt < res ) res= cnt;
158     }
159      return res;
160     
161 
162 }
163  char str[ 6][ 6];
164  int main()
165 {
166      int t,i,j;
167      for(i =  0;i<  4;i++)
168     {
169         scanf( " %s ",str[i]);
170     }
171     init();
172      int f1 =  0,f2 =  0;
173      for(i =  0 ;i<  4;i++)
174     {
175          for(j =  0 ; j <  4;j++)
176         {
177              if(str[i][j] ==  ' b ')
178             {
179                 f1 =  1;
180                 a[i* 4 + j][ 16] =  1;
181             }
182              else
183             {
184                 f2 =  1;
185             }
186         }
187     }
188      /* if(f1 == 0 || f2 == 0)
189      {
190          printf("0\n");
191          return  0;
192      } */
193      int ans = Gauss( 16, 16) ;
194 
195      init();
196      for(i =  0 ;i<  4;i++)
197     {
198          for(j =  0 ; j <  4;j++)
199         {
200              if(str[i][j] ==  ' w ')
201             {
202                 a[i* 4 + j][ 16] =  1;
203             }
204         }
205     }
206      int res = Gauss( 16, 16);
207      if(ans == - 1 && res == - 1)
208     {
209         printf( " Impossible\n ");
210     }
211      else
212     {
213         printf( " %d\n ",min(ans,res)) ;
214     }
215 }

 

题解:

看代码