算法练习 DAY35 || 435. 无重叠区间 763.划分字母区间 56. 合并区间
435. 无重叠区间
给定一个区间的集合,找到需要移除区间的最小数量,使剩余区间互不重叠。
注意: 可以认为区间的终点总是大于它的起点。 区间 [1,2] 和 [2,3] 的边界相互“接触”,但没有相互重叠。
示例 1:
输入: [ [1,2], [2,3], [3,4], [1,3] ]
输出: 1
解释: 移除 [1,3] 后,剩下的区间没有重叠。
示例 2:
输入: [ [1,2], [1,2], [1,2] ]
输出: 2
解释: 你需要移除两个 [1,2] 来使剩下的区间没有重叠。
示例 3:
输入: [ [1,2], [2,3] ]
输出: 0
解释: 你不需要移除任何区间,因为它们已经是无重叠的了。
思路:
按照右边界排序,就要从左向右遍历,因为右边界越小越好,只要右边界越小,留给下一个区间的空间就越大,所以从左向右遍历,优先选右边界小的。从左向右记录非交叉区间的个数。最后用区间总数减去非交叉区间的个数就是需要移除的区间个数了。
 因为已经按照右区间排过序,所以第一个选取的一定是1,然后找到4和6。那么此时不重合区间就是3个,总数-3 就是要移除的个数
因为已经按照右区间排过序,所以第一个选取的一定是1,然后找到4和6。那么此时不重合区间就是3个,总数-3 就是要移除的个数
class Solution {
public:
static bool cmp(const vector<int>& a, const vector<int>& b) {
return a[1] < b[1];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
if (intervals.size() == 0) return 0;
sort(intervals.begin(), intervals.end(), cmp);
//记录非交叉区间的个数
//由于数组不为空 所以至少有一个区间
int count = 1;
int temp = intervals[0][1];
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i][0] >= temp) {
count++;
temp = intervals[i][1];
}
}
return intervals.size() - count;
}
};
/*
注意题干要求的是 : 找到需要移除区间的最小数量
注意!最小
[[1,100],[11,22],[1,11],[2,12]]
这个数组就只要移除两个
但现有逻辑只是在移除 没有考虑最小 不能算是贪心
*/
class Solution {
public:
static bool cmp(const vector<int>& a,const vector<int>& b) {
return a[0] < b[0];
}
int eraseOverlapIntervals(vector<vector<int>>& intervals) {
sort(intervals.begin(), intervals.end(), cmp);
int count = 0;
for (int i = 1; i < intervals.size(); i++) {
if (intervals[i][0] < intervals[i - 1][1]) {
count++;
intervals[i] = intervals[i - 1];
}
}
return count;
}
};
763.划分字母区间
字符串 S 由小写字母组成。我们要把这个字符串划分为尽可能多的片段,同一字母最多出现在一个片段中。返回一个表示每个字符串片段的长度的列表。
示例:
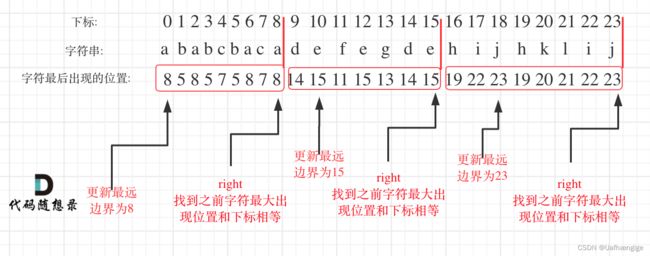
输入:S = "ababcbacadefegdehijhklij"
输出:[9,7,8] 解释: 划分结果为 "ababcbaca", "defegde", "hijhklij"。 每个字母最多出现在一个片段中。 像 "ababcbacadefegde", "hijhklij" 的划分是错误的,因为划分的片段数较少。
提示:
S的长度在[1, 500]之间。
S只包含小写字母 'a' 到 'z' 。
方法一
class Solution {
public:
vector<int> partitionLabels(string s) {
vector<int> hash(27, 0); //使用一个定长数组
for (int i = 0; i < s.size(); i++) {
//统计某个字母出现的最远距离
hash[s[i] - 'a'] = i;
}
int right = 0;
vector<int> result;
int left = 0;
for (int i = 0; i < s.size(); i++) {
right = max(right, hash[s[i] - 'a']);
//找到最远右边界
if (right == i) {
//说明其他字母的边界都在s[i]这个字母以内
//比如 abca hash[0]=3 hash[1]=1 hash[2]=2 hash[3]=3
//i=0时 s[i]=a hash[0]=3 直到i=3之前 right都没有被更新过
result.push_back(right - left + 1);
left = i + 1;
}
}
return result;
}
};
方法二
统计字符串中所有字符的起始和结束位置,记录这些区间,将区间按左边界从小到大排序,找到边界将区间划分成组,互不重叠。找到的边界就是答案。
56. 合并区间
给出一个区间的集合,请合并所有重叠的区间。
示例 1:
输入: intervals = [[1,3],[2,6],[8,10],[15,18]]
输出: [[1,6],[8,10],[15,18]]
解释: 区间 [1,3] 和 [2,6] 重叠, 将它们合并为 [1,6].
示例 2:
输入: intervals = [[1,4],[4,5]]
输出: [[1,5]]
解释: 区间 [1,4] 和 [4,5] 可被视为重叠区间。
注意:输入类型已于2019年4月15日更改。 请重置默认代码定义以获取新方法签名。
思路:
排序按照左边右边都可以
以左边界排序,找重合区域的最大右区间
但有很多细节要注意
class Solution {
public:
vector<vector<int>> merge(vector<vector<int>>& intervals) {
vector<vector<int>> result;
if (intervals.size() == 0) return result;
// 排序的参数使用了lambda表达式
sort(intervals.begin(), intervals.end(),
[](const vector<int>& a, const vector<int>& b)
{return a[0] < b[0]; });
result.push_back(intervals[0]);
for (int i = 1; i < intervals.size(); i++) {
if (result.back()[1] >= intervals[i][0]) {
result.back()[1] = max(result.back()[1], intervals[i][1]);
}
else {
result.push_back(intervals[i]);
}
}
return result;
}
};
自己写的(有两个逻辑漏洞)
class Solution {
public:
static bool cmp(const vector<int>& a, vector<int>& b) {
return a[0] < b[0];
}
vector<vector<int>> merge(vector<vector<int>>& intervals) {
vector<vector<int>> result;
sort(intervals.begin(), intervals.end());
int left = intervals[0][0];
int right = intervals[0][1];
bool flag = false;
for (int i = 1; i < intervals.size(); i++) {
//逻辑漏洞2:
//[[1,4],[4,5]] 如果只有两个 那么该逻辑会返回空
//这个不应该是if 而应该是while 直到找到最后一个能被融合的
//再走到下一步添加结果进result
if (intervals[i][0] <= right) {
//说明有重合区间 更新left
right = intervals[i][1];
if (i == intervals.size() - 1) flag = true;
}
else { //说明不重合
vector<int> temp;
temp.push_back(left);
temp.push_back(right);
result.push_back(temp);
temp.clear();
left = intervals[i][0];
right = intervals[i][1];
//但这个逻辑就会忽略最后一组left 和 right
//要加个flag来做判断
}
}
if (flag == false) {
result.push_back({ intervals[intervals.size() - 1]
[0], intervals[intervals.size() - 1][1] });
}
return result;
}
};