经典数据结构之链表、队列、栈&LinkedList源码分析
经典数据结构之链表、队列、栈&LinkedList源码分析
链表、队列、栈
链表: 相比于数组,链表是一种稍微复杂一点的数据结构,它有三种形式:单链表、双向链表和循环链表。它是以结点的形式存储在内存中,每个结点内部都有数据和指针,指针用来指向前一个或后一个结点,所以它是每个结点通过指针互相串连起来形成的一条链表。在内存中是不连续的,这样更灵活,只要内存空间够我就可以创建链表,而不像数组,必须要有足够的连续内存空间才可以创建。但是也因为它不是连续的所以查找某一位置上的结点的性能就打了折扣,必须通过指针挨个地去遍历。
我们来看一下单链表,每个结点内有两个属性,一个保存结点的数据,一个保存下一个结点地址的指针。通过指针将所有结点串连了起来。如下图,最后一个结点的指针指向空,头结点first指向链表在内存中开始的地址,也就是第一个结点的地址,通过first我们就可以访问每一个结点了

循环链表,是一种特殊的单链表,它的尾结点next指针指向了头结点。当我们要处理的数据具有环形结构的时候就可以使用循环链表。如下图:

双向链表,单链表只有一个next指针指向后继结点,双向链表比单链表多了一个前驱指针用来指向结点的前驱结点。比单链表多了一个指针就会多占用存储空间,但是却方便了很多操作,比如它可以直接定位前驱结点,时间复杂度是O(1)。但是如果单链表要查找前驱结点只能从头开始再遍历一遍了,时间复杂度是O(n),性能很低。如下图所示:

如果头结点的前驱指针指向尾结点,尾结点的后继指针指向头结点,那么就形成了双向循环链表:

从上面几张图中我们可以发现,链表的查找时间复杂度为O(n),因为我们只能顺藤摸瓜去查找。删除、插入的时间复杂度也是O(n),除了头、尾结点,在其他的位置前插入、删除的话我们要先找到指定位置复杂度为O(n),单纯删除、插入的时间复杂度是O(1),所以总的时间复杂度还是O(n)
队列: 我们在排队买票的时候就形成了一个队列,先进者先出,后进者后出,它是一种操作受限的线性表,只有两种基本操作:入队、出队。我们知道最基本的数据结构只有数组和链表,其他的数据结构都是基于这两种来实现的。队列可以用数组来实现,也可以用链表来实现。用数组实现的队列叫顺序队列,用链表实现的队列叫链式队列。
顺序队列:head指向队头,tail指向队尾,因为只能在队头或队尾入队或出队,所以时间复杂度是O(1),空间复杂度是O(1)

链式队列:通过保存head、tail两个指针,入队、出队的时间复杂度O(1)

栈: 当我们早高峰挤地铁的时候,最后一个挤进来的人到了下一站就可以第一个出去了,这就是一种栈结构。它具体后进者先出,先进者后出的特性。它也是一种操作受限的线性表,只允许在一端插入、删除。如何实现一个栈呢,我们也有两种方式,基于数组的顺序栈,基于链表的链式栈。由于只能在一端操作入栈、出栈,所以的它的时间复杂度是O(1),空间复杂度是O(1)

LinkedList源码分析
LinkedList也是java常用的一种集合框架,它实现了List和Deque接口,内部实现是基于链表,所以同时兼备了链表、队列、栈的特性。它是非线程安全的,内部所有操作都是非原子性的,需要使用者自己做同步处理。一般在每个线程中单独创建、使用,比如在方法内部创建,或ThreadLocal中创建(线程隔离)
我们先来看一下它作为List对象的一些属性和方法
属性字段
三个字段都是transient修饰的,不参与序列化,它重写了序列化反序列的方法。内部维护了一个双向链表(有前驱、后继指针),通过first、last头尾指针访问链表结点,链表为空的话头尾指针指向空
//列表中元素的数量
transient int size = 0;
//头结点,指向链表的第一个结点
transient Node<E> first;
//尾结点,指向链表的最后一个结点
transient Node<E> last;
继续看Node结点定义,只有三个字段:前驱、后继、数据域
//存储数据以及前后指针,很明显这是一个双向链表
private static class Node<E> {
//数据
E item;
//后继结点
Node<E> next;
//前驱结点
Node<E> prev;
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
构造函数
有两个构造函数,一个无参默认构造器,和一个传入Collection集合的构造器
//无参构造器,创建一个空结点的列表
public LinkedList() {
}
//传入另外一个集合
public LinkedList(Collection<? extends E> c) {
this();
//将集合所有元素添加到当前LinkedList中
addAll(c);
}
public boolean addAll(Collection<? extends E> c) {
//第一个参数传的是插入的位置,这里size表示最后一个位置
return addAll(size, c);
}
继续看addAll方法
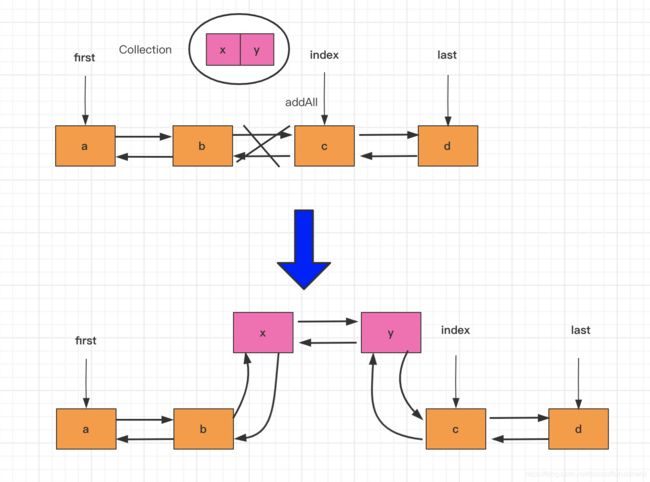
public boolean addAll(int index, Collection<? extends E> c) {
//检查index是否越界,即超出链表范围
checkPositionIndex(index);
//外部集合转化成数组
Object[] a = c.toArray();
int numNew = a.length;
//外部集合是空的话就返回false
if (numNew == 0)
return false;
//临时变量,记录待插入位置的前驱、后继结点
Node<E> pred, succ;
if (index == size) {
//如果是最后一个位置的话,后继指针为空,
//前驱指针指向最后一个结点
succ = null;
pred = last;
} else {
//查找index位置的结点,它作为待插入结点的后继结点
succ = node(index);
//index位置前一个结点就作为待插入结点的前驱结点
pred = succ.prev;
}
//逐个遍历外部集合元素
for (Object o : a) {
//将每个元素构造成一个新的结点,新结点的前驱指针直接指向pred
Node<E> newNode = new Node<>(pred, e, null);
if (pred == null)
//只有在第一个元素插入的时候前驱结点pred才有可能是空的
//如果是空的话它就作为头结点
first = newNode;
else
//前驱结点的后继结点就指向新的这个结点
pred.next = newNode;
//完成以后,新结点就插到了index位置的前一个位置
//此时,新结点就变成了待插入结点的前驱结点
pred = newNode;
}
//到这里succ结点还是原先index位置的结点,它有可能是空的
if (succ == null) {
//如果是空的话尾结点就指向最后插入的那个结点
last = pred;
} else {
//否则的话,succ结点就作为最后一个插入结点的后继结点
pred.next = succ;
succ.prev = pred;
}
//size增加新元素的个数
size += numNew;
//增加修改次数
modCount++;
return true;
}
add方法
在当前链表尾部插入结点,因为只在尾部插入,可以通过last尾指针直接定位到插入的位置,所以时间复杂度为O(1),空间复杂度也为O(1)
//在链表尾部添加结点
public boolean add(E e) {
linkLast(e);
return true;
}
//尾插法,将新的结点插入到尾部
void linkLast(E e) {
final Node<E> l = last;
//构造新结点,新结点的前驱指针指向原来的尾结点
final Node<E> newNode = new Node<>(l, e, null);
//尾结点指针指向新的结点
last = newNode;
if (l == null)
//如果原先的尾结点指针是空的话,说明原先没有结点存在
first = newNode;
else
//否则的话原先尾结点的后继结点变成新插入的结点
l.next = newNode;
//结点个数、修改次数各加1
size++;
modCount++;
}
重载的add方法在指定位置前插入结点,我们必须通过node方法遍历到index位置所在的结点,然后才能插入,所以时间复杂度为O(n),空间复杂度为O(1)
//在指定位置前添加元素
public void add(int index, E element) {
//判断是否越界
checkPositionIndex(index);
//index是最后一个位置的话就插到最后一个尾结点上
if (index == size)
linkLast(element);
else
//插到index位置前面
linkBefore(element, node(index));
}
//在succ结点前插入新元素e
void linkBefore(E e, Node<E> succ) {
//succ的前驱结点
final Node<E> pred = succ.prev;
//新结点的前驱结点指向succ的前驱结点,后继结点指向succ
final Node<E> newNode = new Node<>(pred, e, succ);
//succ的前驱结点指向新的结点
succ.prev = newNode;
if (pred == null)
//如果原先succ的前驱结点的空的话
//那么新插入的结点就是头结点
first = newNode;
else
//否则,succ原先的前驱结点的后继结点就变成了新插入的结点
//新结点就插在了succ跟succ.pred之间
pred.next = newNode;
//元素个数、修改次数各加1
size++;
modCount++;
}
remove方法
根据数据值删除指定结点,我们并不知道待删除的结点所在的位置,所以要先查找,然后再删除对应的结点,所以删除的时间复杂度为O(n),空间复杂度为O(1)
//删除指定结点
public boolean remove(Object o) {
if (o == null) {
//从头开始查找第一个数据为空的结点并删除
for (Node<E> x = first; x != null; x = x.next) {
if (x.item == null) {
unlink(x);
return true;
}
}
} else {
//从头开始查找第一个数据不为空的结点并删除
for (Node<E> x = first; x != null; x = x.next) {
if (o.equals(x.item)) {
unlink(x);
return true;
}
}
}
return false;
}
//删除某个结点x
E unlink(Node<E> x) {
// assert x != null;
//待删除结点的数据对象
final E element = x.item;
//待删除结点的后继结点
final Node<E> next = x.next;
//待删除结点的前驱结点
final Node<E> prev = x.prev;
if (prev == null) {
//如果前驱结点是空的,那么头结点直接指向后继结点
first = next;
} else {
//x结点的前驱结点的后继指针直接指向x结点的后继结点
//相当于绕过了x结点
prev.next = next;
//x结点的前驱指针置空,因为他马上要被删了
x.prev = null;
}
//如果后继结点是空的那么尾结点直接指向前驱结点即可
if (next == null) {
last = prev;
} else {
//否则的话x结点的后继结点的前驱指针指向x结点的前驱结点
next.prev = prev;
//x结点的后继指针置空
x.next = null;
}
//到这里,x结点已经被彻底断开了
//再把他的数据指针置空,方便gc回收
x.item = null;
//链表个数减1
size--;
//修改次数加1
modCount++;
return element;
}
根据索引位置删除指定结点,我们先要遍历到index位置所在的结点然后再删除,所以时间复杂度也是O(n),空间复杂度O(1)
//删除指定结点index
public E remove(int index) {
//检查是否越界
checkElementIndex(index);
return unlink(node(index));
}
//查找index位置对应的结点
//因为链表是内存不连续的,所以我们只能顺藤摸瓜的去查找,所以时间复杂度为O(n),
//空间复杂度为O(1),只需要额外的一个变量记录
Node<E> node(int index) {
//这里作者做了一点优化,如果index小于中间位置的话就从头结点开始顺藤摸瓜
if (index < (size >> 1)) {
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {
//如果index大于中间位置的话就从尾结点开始查找
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
get、set方法
这两个方法都是根据index位置获取、更新,同样的要先遍历到index所在位置的结点,两个方法的时间复杂度都是O(n),空间复杂度O(1)
//根据index索引获取指定结点数据
public E get(int index) {
//检查index是否越界
checkElementIndex(index);
//查找对应index的结点
return node(index).item;
}
//更新对应位置index的结点,只更新该结点的数据
public E set(int index, E element) {
checkElementIndex(index);
//找到对应的结点
Node<E> x = node(index);
//更新结点数据
E oldVal = x.item;
x.item = element;
return oldVal;
}
List相关的方法就分析到这了,其实不难发现,由于链表的特殊结构,增删改查某一结点的时间复杂度都是O(n),除了头尾结点可以直接定位到(O(1))。而由于LinkedList是线程不安全的,在操作插入、删除时都没有做原子同步,会出现并发问题。比如,linkLast(E e)方法在链表尾部添加一个结点,有两个线程A、B同时进入该方法,同时创建两个结点nodeA、nodeB,前驱指针都指向尾部结点last,当线程A执行完代码l.next = newNode后还没跳出当前方法,线程B又执行了l.next = newNode,此时nodeB才是真正的尾结点,而nodeA就掉链了。如下图所示。并发问题在插入、删除时还会有其他很多问题,这里就不一一举例了,请读者朋友自行脑补。

我们再来看一下LinkedList作为Deque实例的一些方法。Deque是一个双端队列,支持在队列的两端添加、删除元素,它扩展了Queue接口,不仅支持队列的常用操作,还支持栈的操作。我们先来看一下作为队列的一些方法,由于很多方法的内部都是复用了上面链表的一些常用方法,所以我们不做过多的解读了。
四个添加方法
addFirst(e)、offerFirst(e)、addLast(e)、offerLast(e)
//在队头插入元素
public void addFirst(E e) {
linkFirst(e);
}
//头插法,将新元素插入到头结点
private void linkFirst(E e) {
final Node<E> f = first;
//将新元素包装成结点,后继结点为原来的头结点
final Node<E> newNode = new Node<>(null, e, f);
//头结点指针指向新的结点
first = newNode;
if (f == null)
//如果原先的头结点是空的,那么说明原先没有结点存在
//这个结点也就是尾结点了,将尾结点指针指向新的结点
last = newNode;
else
//否则的话说明尾结点是存在的
//只要更新原先头结点的前驱指针指向新的结点即可
f.prev = newNode;
//元素数量加1
size++;
//修改次数加1
modCount++;
}
//在队尾插入元素
public void addLast(E e) {
linkLast(e);
}
//队头插入元素
public boolean offerFirst(E e) {
addFirst(e);
return true;
}
//队尾插入元素
public boolean offerLast(E e) {
addLast(e);
return true;
}
四个删除方法
pollFirst()、pollLast()、removeFirst()、removeLast()
//删除队头
public E pollFirst() {
final Node<E> f = first;
return (f == null) ? null : unlinkFirst(f);
}
//删除头结点
private E unlinkFirst(Node<E> f) {
//头结点的数据
final E element = f.item;
//头结点的后继结点
final Node<E> next = f.next;
//头结点数据对象的指针置空,没有了GCRoot指向后头结点的数据对象就会被回收(也有可能在其他地方被使用者引用)
f.item = null;
//头结点的后继指针置空
f.next = null;
//头结点的后继结点升级为头结点
first = next;
if (next == null)
//如果后继结点不存在说明链表没有结点了,尾指针指向空
last = null;
else
//否则,后继的结点的前驱指针置空,此时原先的头结点已经没有指针指向了(如果其他地方也没有的话)
//孤零零飘荡在内存中,下次gc就会被干掉
next.prev = null;
//结点个数减1
size--;
//修改次数加1
modCount++;
return element;
}
//删除队尾
public E pollLast() {
final Node<E> l = last;
return (l == null) ? null : unlinkLast(l);
}
//删除尾结点
private E unlinkLast(Node<E> l) {
//尾结点数据对象
final E element = l.item;
//尾结点的前驱结点
final Node<E> prev = l.prev;
//尾结点的数据指针置空,没有了GCRoot指向后会被回收(也有可能在其他地方被使用者引用)
l.item = null;
//尾结点的前驱指针置空
l.prev = null;
//尾结点的前驱结点就变成了尾结点
last = prev;
if (prev == null)
//如果前驱结点不存在说明链表已经空了
//头结点指向空
first = null;
else
//否则尾结点前驱结点的后继指针置空,此时尾结点没有指针指向了(如果其他地方也没有的话)
//下次gc就会被干掉
prev.next = null;
//链表个数减1
size--;
//修改次数加1
modCount++;
return element;
}
//删除队头
public E removeFirst() {
final Node<E> f = first;
if (f == null)
throw new NoSuchElementException();
//删除头结点即可
return unlinkFirst(f);
}
//删除队尾
public E removeLast() {
final Node<E> l = last;
if (l == null)
throw new NoSuchElementException();
//删除尾结点即可
return unlinkLast(l);
}
四个检查方法
getFirst()、getLast()、peekFirst()、peekLast()这四个方法都是返回元素数不删除结点
//返回头结点的数据,没有删除头结点
public E peekFirst() {
final Node<E> f = first;
return (f == null) ? null : f.item;
}
//返回尾结点的数据,没有删除尾结点
public E peekLast() {
final Node<E> l = last;
return (l == null) ? null : l.item;
}
//获取队列第一个元素
public E getFirst() {
final Node<E> f = first;
if (f == null)
throw new NoSuchElementException();
//直接返回头结点的数据
return f.item;
}
//获取队列最后一个结点的数据
public E getLast() {
final Node<E> l = last;
if (l == null)
throw new NoSuchElementException();
//直接返回尾结点的数据
return l.item;
}
当作栈使用
Deque也可以当作一个栈来使用,它只有两个操作:入栈、出栈。
当我们只在队列的一端插入或者删除时它就是一个栈了
//压栈操作,插入头结点
public void push(E e) {
addFirst(e);
}
//出栈操作,获取头结点并返回
public E pop() {
return removeFirst();
}
序列化与反序列化
clone方法是一种浅克隆,克隆出来的对象内部还是引用了原对象的链表
//浅克隆,克隆的对象共享一份链表
public Object clone() {
//调用父类super方法,克隆对象
LinkedList<E> clone = superClone();
// 初始化所有变量
clone.first = clone.last = null;
clone.size = 0;
clone.modCount = 0;
//将所有结点添加到新对象中,没有创建新的结点,这里共享了一份链表结点
for (Node<E> x = first; x != null; x = x.next)
clone.add(x.item);
return clone;
}
序列化、反序列化是一种深克隆方式,通过反序列化生成的对象其内部数据完全独享
//序列化操作,ObjectOutputStream#writeObject方法会调用到这个
//方法
private void writeObject(java.io.ObjectOutputStream s)
throws java.io.IOException {
//先将非static、transient修饰的字段写入到stream中
//LinkedList的size、node都是transient修饰的,会单独处理
s.defaultWriteObject();
//写入size到stream中
s.writeInt(size);
//按顺序序列化每一个结点
for (Node<E> x = first; x != null; x = x.next)
s.writeObject(x.item);
}
//反序列化,ObjectInputStream#readObject会调用到这个方法
private void readObject(java.io.ObjectInputStream s)
throws java.io.IOException, ClassNotFoundException {
//先读取非static、transient修饰的字段
s.defaultReadObject();
//读取size,对应于上面的s.writeInt(size);
int size = s.readInt();
// 根据size逐个反序列化每个结点并将它串起来
for (int i = 0; i < size; i++)
linkLast((E)s.readObject());
}
结束语:LinkedList的源码分析就到这了,如果感兴趣的话可以帮忙关注一下,后续还会有很多经典集合框架的源码解读,谢谢!