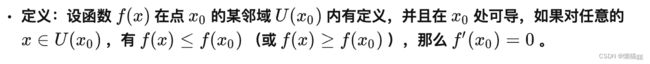微积分(二) 导数与微分
前言
导数反映了函数值相对于自变量的变化快慢程度,而微分则表明当自变量有微小变化时,函数值大体上变化多少
瞬时速度的解决——极限
牛顿采用了一种无限逼近的方法。
平均速度的定义:如果一个物体在一段时间△t内位移了s,它在这段时间内的平均速度是:△s/△t.
由于物体在某一时刻的位移s由时间t决定,因此它是t的函数,可以写成s(t)的形式.如果我们在一个坐标系中用横坐标表示t,纵坐标表示s,那么物体在任意时刻的位移就是一条曲线,如图

如图,当时间间隔△t逐渐变小时,△s/△t的比值会越来越接近t.点的速度。最后当△t趋近于0时,三角形斜边所在的直线,就是曲线在t.点的切线,它的斜率就是物体在t.点的瞬时速度
V ( t ) = lim △ t → 0 △ s / △ t V(t)=\lim\limits_{{△t \to 0}}△s/△t V(t)=△t→0lim△s/△t
通过极限的概念,牛顿将平均速度和瞬时速度联系起来了。这一点在认识论上有很重大的意义,它说明宏观整体的规律和微观瞬时的规律之间并非是孤立的,而是有联系的。
当然,如果只是通过极限思想计算出一个时间点的瞬时速度,比起两千多年前阿基米德用割圆术估算圆周率也没有太多进步。牛顿了不起的地方在于,他认识到函数变化的速率,也就是函数曲线上每一个点切线的斜率,本身又是一种新的函数,他称之为流数,就是我们今天所说的导数,原先的函数也因此被称为原函数。
- 导数的本质,就是对原函数变化快慢的规律性的描述
- 有了导数,人们对函数变化快慢的度量,就从定性估计精确到定量分析了,我们甚至可以准确地度量一个函数在任意一个点的速率变化,也可以对比不同函数的速率变化。
导数

看看下面两个例子

例6.求函数 f ( x ) = ∣ x ∣ f(x)=|x| f(x)=∣x∣在x=0 处的导数。

即函数可导性与连续性的关系

- 如果函数在 y = f ( x ) y=f(x) y=f(x)在点 x x x处可导,则函数必在该点连续
- 一个函数在某点连续却不一定在该点可导
根据导数定义得初等函数求导公式
函数的四则运算的求导法则
反函数的求导法则
复合函数的求导法则

简言之,如果里层函数在 x 0 x_0 x0点处可导,外层函数在相应的 u 0 u_0 u0 处可导,那么复合函数在 x 0 x_0 x0处可导,且导数是外层函数在 u 0 u_0 u0处的导数值乘以里层函数在 x 0 x_0 x0 处的导数值。

隐函数的导数

为什么要讨论隐函数的导数呢?何不先把隐函数显化,然后再求导呢?原因是有时候隐函数显化的过程非常困难,所以不如直接在隐函数的基础上进行求导来的简单。

对 y 5 y^5 y5求导,可以看成是一个复合函数的操作
- g ( y ) = y 5 g(y)=y^5 g(y)=y5
- y = f ( x ) y=f(x) y=f(x)
则 g ′ ( x ) = g ′ ( y ) f ′ ( x ) = 5 y 4 d y d x g'(x)= g'(y)f'(x) = 5y^4\frac{dy}{dx} g′(x)=g′(y)f′(x)=5y4dxdy
由参数方程所确定的函数的导数


有时候很难根据参数方程求出其确定的函数表达式,从而求导函数。所以我们希望可以直接在参数方程的基础上求导,下面我们来讨论如何直接根据参数方程求其确定的函数的导函数。


微分:描述微观世界的工具
什么是微分呢?它其实就是在前面有关速度的例子中提到的,当△t趋近于零时,位移量△s的值。对比一般性的函数y=f(x),我们用dx表示自变量趋于零的情况,用dy表示函数的微分。
如果我们对比一下导数的定义和微分的定义,就可以看出它们讲的其实是一回事,因为dy=f’(x)*dx,因此,我们也经常直接把导数写成:f’(x)=dy/dx
如果我们孤立地看微分少,就是无穷小,定义微分这样一个新概念有什么必要呢?
我们用一个具体的例子来说明。假如你是一个工程师,要建造一个巨大的储油噬,无论增大半径还是增加高度,都有相当大的工程难度。而现在建造经费有限,只能在一个维度上增大储油罐的体积,你应该怎么做呢?
我们知道,圆柱体的体积等于圆周率π乘以半径平方再乘以高度,即 V = π r 2 h V=πr^2h V=πr2h.如果要问圆柱体的体积随半径变化快还是随高度变化快.在没有微分这个概念时,一般人根据直觉,会觉得随半径变化快,因为体积和半径之间是平方关系,而随高度变化只是线性关系。
真实情况是什么样呢?我们可以对这两种变化趋势做量化的对比:在半径和高度特定的条件下,看看半径增长一个很小的单位,体积增加多少;再看看高度增加同样的单位,体积增加多少。先来看半径增长对体积的影响。

所以当储油罐比较"扁平"时,应该增加高度。
微分在近似计算中的应用
微分中值定理
通过研究函数 f ( x ) f(x) f(x),总结出一定的规则
费马(Fermat)引理
罗尔(Rolle)定理
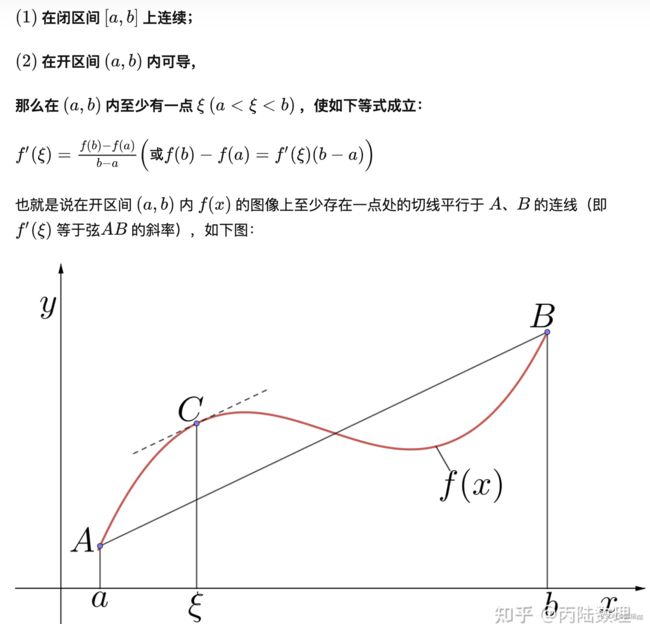
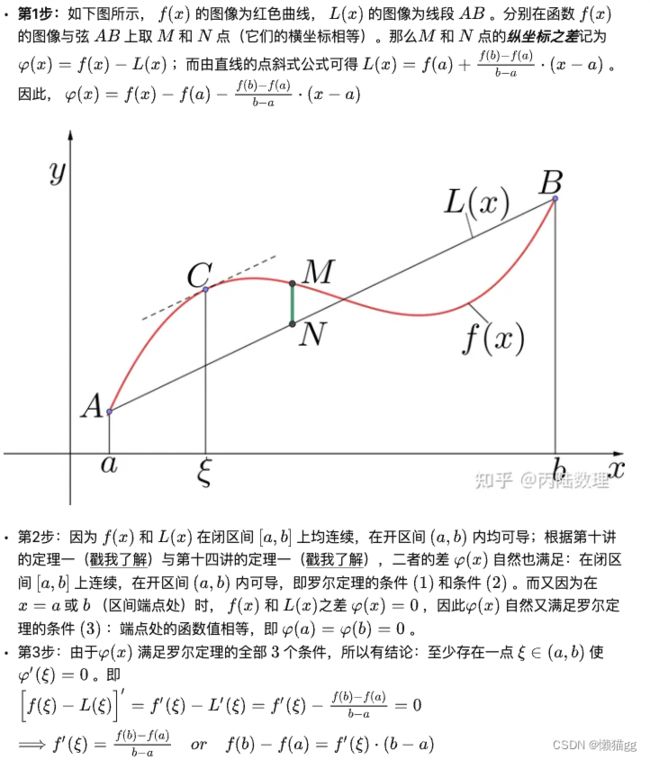
拉格朗日(Lagrange)中值定理
柯西(Cauchy)中值定理
主要参考
《第十三讲 导数的概念》
《第十四讲 函数的求导法则》
《第十六讲 隐函数和参数方程所确定函数的导数》
《第十七讲 函数的微分》
《第十九讲 微分中值定理》
《微分和导数的关系是什么》