面试复习——数据结构(六):数组和广义表
文章目录
- 数组
-
- 数组的类型定义
-
- 一维数组/向量(线性结构)
- 二维数组/矩阵/阵列(非线性结构)
- n维数组/n维空间
- 数组实现
- 特殊矩阵的压缩存储(到数组)
-
- Toeplitz矩阵
- 对称矩阵
- 三对角矩阵
- 稀疏矩阵
-
- 矩阵转置——三元组顺序表/有序的双下标法
- 矩阵相乘——行逻辑联接的顺序表
- 矩阵相加——十字链表
- 广义表 Generalized list (非线性结构)
-
- 广义表的类型定义
- 广义表的链式表示
-
- 表头表尾分析法/头尾链表存储结构
- 子表分析法
- 广义表的操作实现(递归)
数组
数组的类型定义
数组作为逻辑结构,是组织数据的一种方式
数组是相同类型的数据元素的集合,元素的下标一般具有固定的下界和上界,采用顺序存储结构实现
一旦建立数组,数据元素的个数与元素之间的关系就不再发生变动
数组作为存储结构可以作为其他多种逻辑结构,如线性表、树、图等的顺序存储表示
一维数组/向量(线性结构)
// 静态数组
#define maxSize 100
ElemType A[maxSize]; //定义时指定数组大小
// 动态数组
ElemType *A;
A=(ElemType *)malloc(maxSize * sizeof(ElemType));
if(!A) return false;
二维数组/矩阵/阵列(非线性结构)
typedef T array2[m][n]; //T为元素类型
等价于:
typedef T array1[n]; //列向量类型
typedef array1 array2[m]; //二维数组类型
每个数组元素有两个直接前驱(行方向一个、列方向一个),两个直接后继(行方向一个、列方向一个)
二维数组不是线性结构,是非线性结构
n维数组/n维空间
多维数组是一维数组的推广
多维数组的特点是每一个数据元素受多个线性关系的约束,每一个数据元素可以有多个直接前驱和多个直接后继
令n维数组第i维的长度为 _ bi
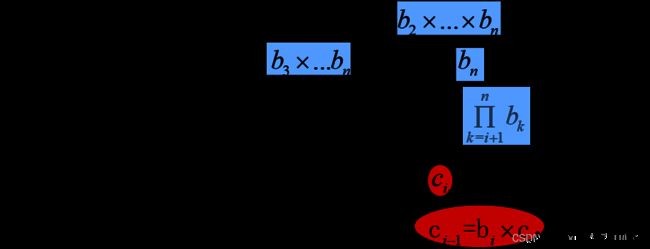
一旦确定了数组的各维的长度, _ ci(常量基址)就是常数,故存取数组中任一元素的时间相等
数组实现
Typedef struct{
ElemType *base;
int dim;
int *bounds; //数组各维的大小
int *constants; //数组映像函数常量基址ci
} Array;
Status InitArray (Array &a, int dim, …);
Status DestroyArray (Array &A);
Status Value (Array A, ElemType &e, …);//取值函数
Status Assign (Array &A, ElemType e, ….);) //赋值函数
#include PS:VA_LIST 是在C语言中解决变参问题的一组宏,变参问题是指参数的个数不定,可以是传入一个参数也可以是多个;可变参数中的每个参数的类型可以不同,也可以相同;可变参数的每个参数并没有实际的名称与之相对应,用起来是很灵活。
Status Locate(Array A, va_list ap, int &off) {
// 若 ap 指示的各下标值合法,则求出该元素在 A 中相对地址 off
off = 0;
for ( i=0; i < A.dim; ++i) {
ind = va_arg(ap,int) ;
if ( ind < 0 || ind >= A.bounds[i] )
return OVERFLOW;
off += A.constants[i] * ind;
}
return OK;
}
Status Value(Array A, ElemType &e, …) {
// 若各下标不超界,则 e 赋值为所指定的 A 的元素值,并返回OK
va_start(ap, e);
if ( ( results = Locate(A, ap, off) ) <= 0 )
return result;
e = * ( A.base + off );
return OK;
}
特殊矩阵的压缩存储(到数组)
特殊矩阵:元素之间存在某种特殊结构关系的矩阵
特殊矩阵的压缩存储:对可以不存储的元素,如零元素或对称元素,不再存储,以节省存储空间
;操作方便
Toeplitz矩阵
该矩阵中,其任何一条对角线的元素取相同值

Toeplitz(0,1,-1):主对角线元素是1、主对角线上面第一个对角线的元素是-1、其它元素是0的矩阵

对称矩阵
元素关于主对角线对称,即, = , 0 ≤ , ≤ − 1 _{}=_{},0≤,≤−1 aij=aji,0≤i,j≤n−1
存储策略:只存对角线及对角线以上的元素,或者只存对角线或对角线以下的元素,前者称为上三角矩阵,后者称为下三角矩阵
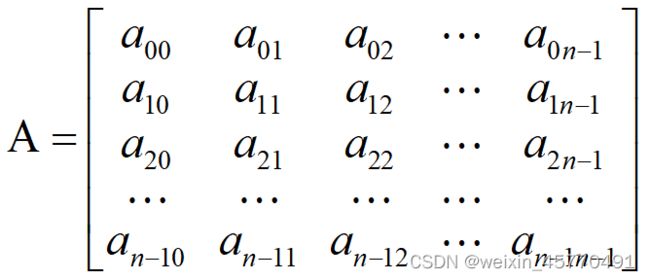
行序优先压缩存储下三角矩阵
行序为主序进行存储给定任一组下标 ( i , j ) (i,j) (i,j)相应的存储位置k为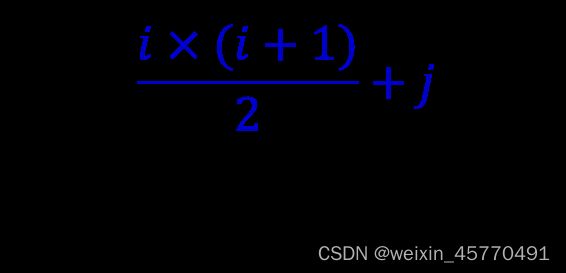

三对角矩阵
除主对角线及在主对角线上下最临近的两条对角线上的元素外,所有其它元素均为0
三条对角线上的元素 a i j a_{ij} aij满足: 0 ≤ ≤ − 1 , − 1 ≤ ≤ + 1 0≤≤−1, −1≤≤+1 0≤i≤n−1,i−1≤j≤i+1,总共有 3 n − 2 3n-2 3n−2个非零元素
将三对角矩阵A 映射到压缩数组B,元素 A [ i ] [ j ] A[i][j] A[i][j]在 B 中位置: k = 2 × i + j k = 2 × i + j k=2×i+j

将压缩数组B映射到三对角矩阵A
若元素 A [ i ] [ j ] A[i][j] A[i][j]在数组 B存放于第 k 个位置,则有
= ⌊ ( + 1 ) / 3 ⌋ , = − 2 × =⌊(+1)/3⌋,=−2× i=⌊(k+1)/3⌋,j=k−2×i
稀疏矩阵
假设 m 行 n 列的矩阵含 t 个非零元素
定义稀疏因子为$ = /(×)$
通常认为 δ ≤ 0.05 δ≤0.05 δ≤0.05的矩阵为稀疏矩阵
稀疏矩阵的基本操作:转置,加法,乘法,拷贝
实现:
稀疏矩阵:由表示非零元的一系列三元组及其行数、列数唯一确定
- 矩阵A的一个非零元素:由三元组 ( i , j , ) (i, j, _{}) (i,j,aij) 唯一确定
稀疏矩阵的压缩存储
- 三元组顺序表/三元组表:矩阵转置
- 行逻辑联接的顺序表:矩阵相乘
- 十字链表:矩阵相加
矩阵转置——三元组顺序表/有序的双下标法
#define MAXSIZE 12500
typedef struct {
int i, j; //该非零元的行下标和列下标
ElemType e; // 该非零元的值
} Triple; // 三元组类型
typedef struct {
Triple data[MAXSIZE + 1];
int mu, nu, tu;
//矩阵的行数、列数和非零元素个数
} TSMatrix; // 稀疏矩阵类型
//非零元在表中按行序有序存储
//便于进行依行顺序处理的矩阵运算
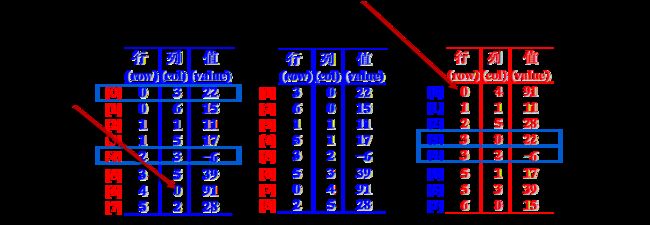
稀疏矩阵M转置成T:
按照T中的三元组的次序依次在M中找到相应的三元组进行转置,也就是,按照矩阵M的列序进行转置
为了找到M中的每一列中所有的非零元素,需要对其三元组表M.data从第一行起整个扫描一遍,由于M.data是以M的行序为主序来存放每个非零元素的,由此得到的恰好是T.data应有的顺序
PS:原矩阵是以行序为先的,保证了扫描时转置矩阵的行序次序
TransposeMatrix的时间复杂度为 O (M.nuM.tu)
当M.tu 和 M.muM.nu 同数量级时,
TransposeMatrix的时间复杂度为O(M.mu*M.nu2)
Status TransposeMatrix(TSMarix M, TSMatrix &T){
//求M矩阵的转置,结果由T返回
T.mu = M.nu; T.nu = M.mu; //矩阵的行数、列数互换
T.tu = M.tu
if (T.tu) {
q =0;//转置矩阵的元素号
for (col = 0; col < M.nu; col++) //以转置矩阵的行序为先
for (p = 0; p < M.tu; p++)
if (M.data[p].j== col) {
T.data[q].i = M.data[p].j;
T.data[q].j = M.data[p].i;
T.data[q].e = M.data[p].e
q++;
}
}
return OK;
}
稀疏矩阵的快速转置:
预先求得原矩阵M 每一列(即T中每一行)的第一个非零元在T中 的位置,那么,对M转置扫描时,立即确定在转置矩阵T三元组表中的位置,并装入它
为加速转置速度,建立辅助数组 num和 cpot
- num[col]:记录矩阵转置前各列(即转置矩阵各行)非零元素个数
- cpot[col]:记录各列非零元素在转置三元组表中开始存放位置
时间复杂度为O(M.nu+M.tu)
Status FastTransposeSMatrix(TSMatrix M, TSMatrix &T){
T.mu = M.nu; T.nu = M.mu; T.tu = M.tu;
if (T.tu) {
for (col=0; col<M.nu; ++col)
num[col] = 0;
for (t=0; t<M.tu; ++t)
++num[M.data[t].j];
cpot[0] = 0;
for (col=1; col<M.nu; ++col)
cpot[col] = cpot[col-1] + num[col-1];
for (p=0; p<M.tu; ++p) {
col = M.data[p].j;
q = cpot[col]; //找该元素在T中的位置
T.data[q].i = M.data[p].j;
T.data[q].j = M.data[p].i;
T.data[q].e = M.data[p].e;
++cpot[col];
}
} // if
return OK;
} // FastTransposeSMatrix
矩阵相乘——行逻辑联接的顺序表
行逻辑联接的顺序表:修改前述的稀疏矩阵的结构定义,增加一个数据成员rpos,指示各行第一个非零元素的位置
#define MAXMN 500
typedef struct {
Triple data[MAXSIZE + 1];
int rpos[MAXMN + 1];
//各行第一个非零元的位置表
int mu, nu, tu;
} RLSMatrix; // 行逻辑链接顺序表类型
// 取值操作:给定一组下标(r, c),求矩阵中对应元素值
ElemType Value(RLSMatrix M, int r, int c) {
//给定行和列坐标(r, c),求取矩阵元素的值
p = M.rpos[r];
while (M.data[p].i==r &&M.data[p].j < c)
p++;
if (M.data[p].i==r && M.data[p].j==c)
return M.data[p].e;
else return 0;
} // value

稀疏矩阵相乘
主要对M矩阵的非零元素做处理
对每一个非零元,找M的列号和N的行号对应的元素相乘
对Q的元素一行一行的进行处理

M.rpos[]={0,2,4,7}是在非零元素数组M.data中的位置
N.rpos[]={0,1,3,4,4}
Status MultSMatrix(RLSMatrix M, RLSMatrix N, RLSMatrix &Q) {
if (M.nu != N.mu) return ERROR;
Q.mu = M.mu; Q.nu = N.nu; Q.tu = 0;
if (M.tu*N.tu != 0) { // Q是非零矩阵
for (arow=0; arow<M.mu; ++arow) {
// 处理M的每一行
ctemp[ ] = 0; // 当前行各元素累加器清零
Q.rpos[arow] = Q.tu+1;
for (p=M.rpos[arow]; p<M.rpos[arow+1];++p) {
//对当前行中每一个非零元
brow=M.data[p].j;
if (brow < N.mu) t = N.rpos[brow+1];
else { t = N.tu+1; }
for (q=N.rpos[brow]; q< t; ++q) {
ccol = N.data[q].j; // 乘积元素在Q中列号
ctemp[ccol] += M.data[p].e * N.data[q].e;
} // for q, 计算Q中第arow行的积并存入ctemp[]
} // 求得Q中第crow( =arow)行的非零元
for (ccol=0; ccol<Q.nu; ++ccol) //将ctemp[]中非零元素压缩存储到Qdata
if (ctemp[ccol]) {
if (++Q.tu > MAXSIZE) return ERROR;
Q.data[Q.tu] = {arow, ccol, ctemp[ccol]};
} // if
} // for a row
} // if
return OK;
} // MultSMatrix
矩阵相加——十字链表
当矩阵的非零元个数和位置在操作中变化较大时,就不宜采用顺序存储结构来表示三元组的线性表,而是采用链式存储结构表示三元组的线性表
每个非零元由一个含5个域的结点表示(i, j, e, right, down)
当矩阵的非零元个数和位置在操作中变化较大时,就不宜采用顺序存储结构来表示三元组的线性表,而是采用链式存储结构表示三元组的线性表
每个非零元由一个含5个域的结点表示(i, j, e, right, down)
typedef struct OLNode{
int i, j;
ElemType e;
struct OLNODE *right, *down;
} OLNode, *Olink;
typedef struct{
//行和列链表 头指针向量的基址
Olink *rhead, *chead;
in mu, nu, tu;
} CrossList
// 基于十字链表创建矩阵
Status CreatSMatrix_OL(CrossList &M) {
if (M) Free(M);
scanf(&m, &n, &t); M.mu =m; M.nu=n; M.tu=t;
if (!(M.rhead=(Olink *)malloc((m+1)*sizeof(OLink)))) exit(OVERFLOW);
if ((!(M.chead=(Olink *)malloc((n+1)*sizeof(OLink)))) exit(OVERFLOW);
Mrhead[ ] = M.chead[ ] = NULL;
for (scanf(&i, &j, &e); i!=0; scanf(&i, &j, &e)) {
if ((p=(OLNode *)malloc(sizeof(OLNode)))) exit(OVERFLOW);
p->i=i; p->j=j; p->e=e; //生成OLNode结点
if (M.rhead[i] == NULL || M.rhead[i]->j>j){
p->right = M.rhead[i]; M.rhead[i] = p;
}else{
for (q= M.rhead[i]; (q->right) && q->right->j < j; q=q->right) ;
p->right = q->right; q->right = p;
}
if (m.chead[j]==NULL || M.chead[j]->i>i){
p->down = M.chead[j]; M.chead[kj]=p;
}else{
for (q=M.chead[j]; (q->down) && q->down->i < i; q=q->down) ;
p->down = q->down; q->down = p;
}
}
}

从矩阵的第一行起逐行进行
对每行都从行表头出发,分别找到A和B在该行中的第一个非零元节点pa、pb,将两者进行比较,然后分4种情况进行处理:
- 若
pa==NULL || pa->j > pb->j,则:新增_ ,其值为_ - 若
pa->j < pb->j,则:pb++ - 若
pa->j==pb->j &&pa->e+pb->e!=0,则_ = _ + _ - 若
pa->j ==pb->j &&pa->e+pb->e==0,则删除pa
广义表 Generalized list (非线性结构)
广义表的类型定义
广义表是n(n≥0 )个表元素组成的有限序列,记作:(_,_,_,…,_)
- LS 是表名,_ (0≤i≤1)是表元素,它可以是广义表(称为子表),也可以是数据元素(称为原子)
- 广义表的长度:最外层包含的元素个数
- 空表:长度(n)为0的广义表
- 当LS非空(即长度大于 0)时,表的第一个表元素称为广义表的表头(head),而其它表元素组成的表称为广义表的表尾(tail)
- 广义表的深度:所含括弧的重数
原子的深度为 0,空表的深度为 1
广义表的深度=Max {子表的深度} +1
结构特点:
- 广义表中的数据元素有相对次序,这个顺序不能交换——类似线性结构
- 广义表是递归定义的线性结构
广义表是一个多层次的线性结构
广义表可以是一个递归的表 - 广义表可以共享

任何一个非空广义表LS = ( a1, a2, …, an)均可分解为:
- 表头 Head(LS) = a1
- 表尾 Tail(LS) = (a2, …, an)
广义表的链式表示
广义表中元素可以是原子或者广义表
用Union类型表示:表结点,原子结点
构造存储结构的两种分析方法
- 表头表尾分析法
- 子表分析法
表头表尾分析法/头尾链表存储结构
若广义表不空,则可分解为表头和表尾;反之,一对确定的表头和表尾可唯一确定广义表

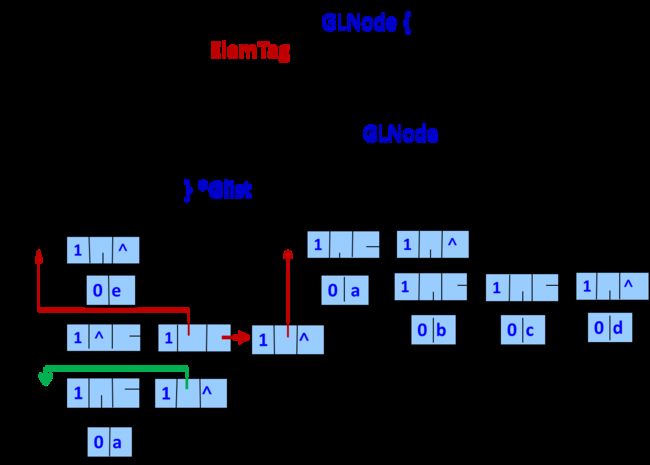
typedef enum {ATOM, LIST} ElemTag;
typedef struct GLNode {
ElemTag tag; // ATOM or LIST
union { //原子结点和表结点的联合部分
AtomType atom;
struct {struct GLNode *hp, *tp;} ptr;
//ptr.hp, ptr.tp指向表结点的表头、表尾
}
} *Glist;
子表分析法
typedef enum {ATOM, LIST} ElemTag;
typedef struct GLNode {
ElemTag tag; // ATOM or LIST
union { //原子结点和表结点的联合部分
AtomType atom;
struct GLNode *hp;//指向子表的指针
};
struct GLNode *tp;
//指向同一层下一个表元素结点的指针
} *Glist;
广义表的操作实现(递归)
广义表的特点
- 广义表 = 表头 + 表尾
- 广义表 = 子表1 + 子表2 + ··· + 子表n
递归(分而治之)——递归算法设计中的关键问题是如何将一个子问题的解组合成原问题的解
//创建和销毁
InitGList(&L); //创建空的广义表
CreateGList(&L, S); //由字符串创建广义表
DestroyGList(&L);
//插入、删除、拷贝
InsertFirst_GL(&L, e); //插入e成L的第一个元素
DeleteFirst_GL(&L, &e);
CopyGList(&T, L);//将广义表L复制到T
//状态函数
GListLength(L); GListDepth(L);
GListEmpty(L); GetHead(L); GetTail(L);
//遍历
Traverse_GL(L, Visit());
创建广义表
设广义表 L以字符串 S = (_1,_2,_3,…,_) 的形式给出,为L建立相应的存储结构
基本项:
- 置空广义表 当 S 为空串
- 建立原子结点的子表 当S为单字符串时
递归项:
- 由于S中的每个子串_i定义了 L 的一个子表,从而产生 n 个子问题,即,分别由这 n个子串 (递归)建立 n 个子表,再组合成一个广义表
void CreateGList(Glist &L, SString S) {
if (!strComp(S,”()”)) L = NULL; // 创建空表
else {
// 生成表结点
if(!(L=(Glist)malloc(sizeof(GLNode)) )) exit(OVERFLOW)
if (StrLen(S)==1){//建立单原子广义表
L->tag=ATOM, L->atom = S; }
else {
L->tag=List; p=L;
//设sub为 脱去串 S 最外层括弧的子串
StrSubStr(sub, S,2,StrLen(S)-1);
//为sub中所含n个子串建立n个子表
do { //重复建n个子表
//分离出子表串hsub=I
Sever(sub, hsub);
//创建由串hsub定义的广义表pptr.hp
CreateGList(p->ptr.hp, hsub);
q=p;
if (!IsStrEmpty(sub) {
//余下的表不为空
if(!(p=(GLNode*)malloc(sizeof(GLNode)) )) exit(OVERFLOW);
//建下一个子表的表结点*(p->ptr.tp)
p->tag = LIST; q->ptr.tp=p;
}
} while (!IsStrEmpty(sub));
q->ptr.tp = NULL; // 表尾为空表
} // else
}//else
return OK;
}
Status Sever(SString &str, SString &hstr) {
//将非空串str分割为两部分:hstr为第一个逗号之前的子串,str为之后的子串
n = StrLength(str);
i=0; k=0; //k:尚未配对的左括号个数
do{
++i;
StrSubStr(ch, str, i, 1); //取一个字符
if ( ch==‘(’ ) ++k;
else ( ch==‘)’ ) --k;
}while ( i<n && (ch!=‘,’ || k!=0) );
if (i<n){ //遇到逗号或括号
StrSubStr(hstr, str, 1, i-1);
StrSubStr(str, str, i+1, n-i);
}
else { StrCopy(hstr, str); StrClear(str); }
} //sever
求广义表的深度
思路:将广义表(_,_,_,…,_)分解成 n 个子表,分别(通过递归)求得每个子表的深度
广义表的深度=Max {子表的深度} +1
基本项:
- depth(LS)=1 当LS为空表
- depth(LS)=0 当LS为原子
递归项:
- d e p t h ( L S ) = 1 + m a x ≤ ≤ { ( ) } depth(LS)=1+max_{≤≤}\{(_)\} depth(LS)=1+max1≤i≤n{depth(ai)}
int GlistDepth(Glist L) { //返回指针L所指的广义表的深度
if (!L) return 1;
if (L->tag == ATOM) return 0;
for (max=0, pp=L; pp;
pp=pp->ptr.tp) { //求以pp
//ptr.hp为头指针的子表深度
dep = GlistDepth(pp->ptr.hp);
if (dep > max) max = dep;
}
//非空表的深度是各元素深度的最大值加1
return max + 1;
} // GlistDepth
复制广义表
将广义表L分解成表头和表尾两部分,分别(递归)复制求得新的表头和表尾
新的广义表T由新的表头和表尾构成
基本项:
- InitGList(T) 当L为空表
递归项:
- COPY(表头){复制表头}
- COPY(表尾) {复制表尾}
Status CopyGList(Glist &T, Glist L) {
if (!L) T = NULL; // 复制空表
else {
//建立表结点
if ( !(T =(GList)malloc(sizeof(GLNode))))
exit(OVERFLOW);
T->tag = L->tag;
if (L->tag == ATOM)
T->atom = L->atom; //复制单原子
else {
CopyGList (T->ptr.hp, L->ptr.hp);
//复制L->ptr.hp到T->ptr.hp
CopyGList (T->ptr.tp, L->ptr.tp);
//复制L->ptr.tp到T->ptr.tp
}
} // else
return OK;
} // CopyGList
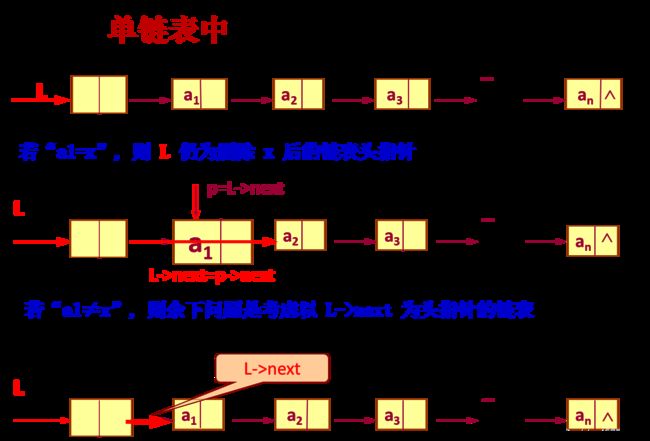
// 删除单链表中所有值为x 的数据元素
void delete(LinkedList &L, ElemType x) {
// 删除以L为头指针的带头结点的单链表中
// 所有值为x的数据元素
if (L->next) {
if (L->next->data==x) {
p=L->next; L->next=p->next;
free(p); delete(L, x);
}
else delete(L->next, x);
}
} // delete
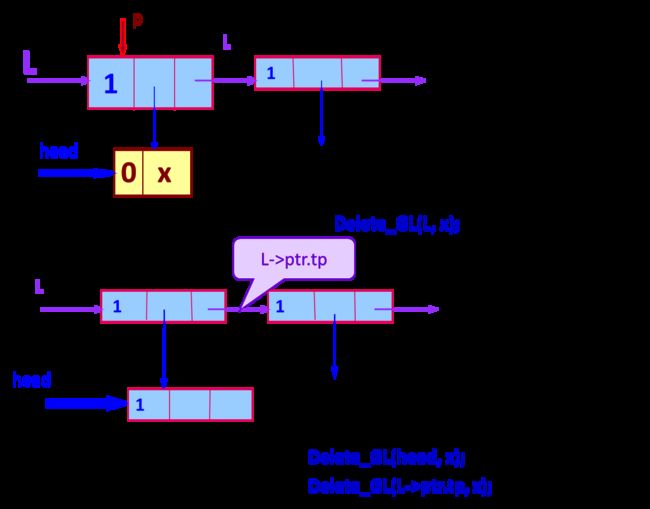
//广义表的数据元素可能还是个广义表;删除时,不仅要删除原子结点,还需要删除相应的表结点
void Delete_GL(Glist&L, AtomType x) {
//删除广义表L中所有值为x的原子结点
if (L) {
head = L->ptr.hp; // 考察第一个子表
if ((head->tag == Atom) && (head->atom == x)){
p=L; L = L->ptr.tp; //修改指针
free(head); //释放原子结点
free(p); //释放表结点
Delete_GL(L, x); //递归处理剩余表项
} // 删除原子项 x的情况
else {
if (head->tag == LIST) {//该项为广义表
Delete_GL(head, x);
Delete_GL(L->ptr.tp, x);
}
}// 第一项没有被删除的情况
}
} // Delete_GL