【力扣热题100,个人刷题笔记---中】
接上文,为力扣刷题个人笔记
二叉树
543.二叉树的直径(简单)
给你一颗二叉树的节点,返回该树的直径。
二叉树的直径是指树中任意两个节点之间最长路径的长度。这条路径可能经过也可能不经过根节点root。
两节点之间的路径长度由它们之间边数表示。

输入:root = [1,2,3,4,5]
输出:3
解释:3 ,取路径 [4,2,1,3] 或 [5,2,1,3] 的长度。
思路:来自力扣官方
深度优先搜索
首先我们知道一条路径的长度为该路径经过的节点数减一,所以求直径(即求路径长度的最大值)等效于求路径经过节点数的最大值减一。
而任意一条路径均可以被看作由某个节点为起点,从其左儿子和右儿子向下遍历的路径拼接得到。

如图我们可以知道路径 [9, 4, 2, 5, 7, 8] 可以被看作以 222 为起点,从其左儿子向下遍历的路径 [2, 4, 9] 和从其右儿子向下遍历的路径 [2, 5, 7, 8] 拼接得到。
假设我们知道对于该节点的左儿子向下遍历经过最多的节点数 L (即以左儿子为根的子树的深度) 和其右儿子向下遍历经过最多的节点数 R (即以右儿子为根的子树的深度),那么以该节点为起点的路径经过节点数的最大值即为 L+R+1。我们记节点 node为起点的路径经过节点数的最大值为 dnode那么二叉树的直径就是所有节点 dnode的最大值减一。
即:经过某个节点的最大路径长度,为其左子树的深度L+右子树的深度R+1。
某树的直径就是该树中最大路径长度-1。
算法流程:构造递归函数,
class Solution {
public:
int deepOfBinaryTree(TreeNode* root){
//深度优先遍历,构造递归函数
//递归终止条件
if(!root) return 0;
//递归函数
return max(deepOfBinaryTree(root->left),deepOfBinaryTree(root->right))+1;
}
int diameterOfBinaryTree(TreeNode* root) {
//递归判断经过每个节点的最大路径长度
//递归终止条件
if(!root) return 0;
//直径等于经过某节点的左右子树深度和的最大值
int currentDiameter = deepOfBinaryTree(root->left)+deepOfBinaryTree(root->right);
int leftDiameter = diameterOfBinaryTree(root->left);
int rightDiameter = diameterOfBinaryTree(root->right);
return max(currentDiameter,max(leftDiameter,rightDiameter));
}
};
通过了验证正确,但是效率低下,原因在于用了两个递归,力扣官方给的解答将两个递归整合为一个递归函数。
时间:24ms,5.9%
空间:19.71MB,13.43%
lass Solution {
int ans;
int depth(TreeNode* rt){
if (rt == NULL) {
return 0; // 访问到空节点了,返回0
}
int L = depth(rt->left); // 左儿子为根的子树的深度
int R = depth(rt->right); // 右儿子为根的子树的深度
ans = max(ans, L + R + 1); // 计算d_node即L+R+1 并更新ans
return max(L, R) + 1; // 返回该节点为根的子树的深度
}
public:
int diameterOfBinaryTree(TreeNode* root) {
ans = 1;
depth(root);
return ans - 1;
}
};
时间复杂度:O(N),12ms,47.33%
空间复杂度:O(N),19.55MB,32.82%
102.二叉树的层序遍历(中等)(利用队列实现广度优先遍历的典型)
给你二叉树的根节点root,返回其节点值的层序遍历。(即逐层地,从左到右访问所有节点)。
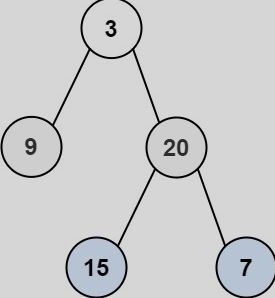
输入:root = [3,9,20,null,null,15,7]
输出:[[3],[9,20],[15,7]]
思路:二叉树的广度优先遍历,利用队列实现
class Solution {
public:
vector<vector<int>> levelOrder(TreeNode* root) {
vector<vector<int> > ans;
if(!root) return ans;
queue<TreeNode* > Q; //队列存储每一层的节点
Q.push(root);
while(!Q.empty()){
int sz = Q.size();
vector<int> tempAns; //存储每一层的ans
while(sz > 0){
TreeNode* node = Q.front();//node指向Q队列的头
tempAns.push_back(node->val);
if(node->left) Q.push(node->left);
if(node->right) Q.push(node->right);
Q.pop();
sz -=1;
}
ans.push_back(tempAns);
}
return ans;
}
};
时间复杂度:O(N),12ms,13.74%
空间复杂度:O(M),13.44MB,13.35%。M为最大层的节点数
108.将有序数组转换为平衡二叉搜索树(简单)
平衡:任意节点的左子树和右子树的高度差不大于1
二叉搜索树:任意节点的值大于左节点,小于右节点
给你一个整数数组nums,其中元素已经按升序排列,请你将其转换为一棵高度平衡二叉搜索树。高度平衡二叉树是一棵满足【每个节点的左右两个子树的高度差的绝对值不超过1】的二叉树
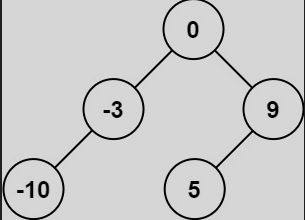
输入:nums = [-10,-3,0,5,9]
输出:[0,-3,9,-10,null,5]
解释:[0,-10,5,null,-3,null,9] 也将被视为正确答案:

思路:递归,将数组中间元素作为根节点。数组左边元素插入到左子树,右边元素插入到右子树。
class Solution {
public:
TreeNode* arrayTOBSTHelper(vector<int>& nums, int start, int end){
//该函数用于递归辅助函数
//终止条件
if(end < start) return nullptr;
//递归函数
int mid = (start + end)/2;
TreeNode* root = new TreeNode(nums[mid]);
root->left = arrayTOBSTHelper(nums,start,mid-1);
root->right = arrayTOBSTHelper(nums,mid+1,end);
return root;
}
TreeNode* sortedArrayToBST(vector<int>& nums) {
return arrayTOBSTHelper(nums,0,static_cast<int>(nums.size())-1); //static_cast类型转换函数,将后面的转为int
}
};
时间复杂度:O(N),12ms,74.14%
空间复杂度:O(N),20.61MB,38.47%
98.验证二叉搜索树(中等)
给你一个二叉树的根节点 root,判断其是否是一个有效的二叉搜索树。
有效 二叉搜索树的定义如下:
- 节点的左子树只包含小于当前节点的数。
- 节点的右子树只包含大于当前节点的数。
- 所有左子树和右子树自身必须也是二叉搜索树。
思路:递归实现,对于每个节点而言,其左子树的值<当前节点的值<右子树的值
class Solution {
public:
bool isValidBST(TreeNode* root) {
//递归实现
//递归终止条件
if(!root) return true;
//递归函数
bool rootIsBST = true;
if(root->left) rootIsBST = rootIsBST && root->left->val < root->val;
if(root->right) rootIsBST = rootIsBST && root->val < root->right->val;
return rootIsBST && isValidBST(root->left) && isValidBST(root->right);
}
};
思路实现错误,只能保证每个节点的左节点<当前节点<右节点
不能保证左右子树中只有包含小于/大于当前节点的数
官方思路:
要解决这道题首先我们要了解二叉搜索树有什么性质可以给我们利用,由题目给出的信息我们可以知道:如果该二叉树的左子树不为空,则左子树上所有节点的值均小于它的根节点的值; 若它的右子树不空,则右子树上所有节点的值均大于它的根节点的值;它的左右子树也为二叉搜索树。
这启示我们设计一个递归函数 helper(root, lower, upper) 来递归判断,函数表示考虑以 root 为根的子树,判断子树中所有节点的值是否都在 (l,r)的范围内(注意是开区间)。如果 root 节点的值 val 不在 (l,r)的范围内说明不满足条件直接返回,否则我们要继续递归调用检查它的左右子树是否满足,如果都满足才说明这是一棵二叉搜索树。
那么根据二叉搜索树的性质,在递归调用左子树时,我们需要把上界 upper 改为 root.val,即调用 helper(root.left, lower, root.val),因为左子树里所有节点的值均小于它的根节点的值。同理递归调用右子树时,我们需要把下界 lower 改为 root.val,即调用 helper(root.right, root.val, upper)。
函数递归调用的入口为 helper(root, -inf, +inf), inf 表示一个无穷大的值。
思路二:中序遍历,(左根右)得到的是一个升序的数组,则说明是二叉搜索树。
class Solution {
public:
bool isValidBST(TreeNode* root) {
stack<TreeNode*> stack; //建立栈来存储所有左节点
long long inorder = (long long)INT_MIN - 1; //inorder初始化为最小的int
while (!stack.empty() || root != nullptr) {
while (root != nullptr) { //如果root为非空指针,则入栈并向左遍历
stack.push(root);
root = root -> left;
}
root = stack.top(); //root重定位到栈头节点
stack.pop();
// 如果中序遍历得到的节点的值小于等于前一个 inorder,说明不是二叉搜索树
if (root -> val <= inorder) {//如果root值小于等于前一个inorder值,则说明不是升序序列
return false;
}
inorder = root -> val; //进入下一次迭代
root = root -> right;
}
return true;
}
};
时间复杂度: 12ms,63.42%
空间复杂度:21.21MB,9.16%
二叉搜索树中第K小的元素(中等)
给定一个二叉搜索树的根节点root,和一个整数k,请你设计一个算法查找其中第k个最小元素(从1开始计数)
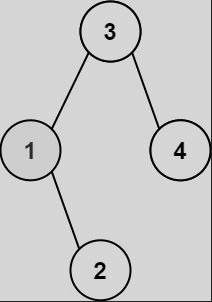
输入:root = [3,1,4,null,2], k = 1
输出:1
思路:二叉搜索树的中序遍历,只输出第k个值即可
lass Solution {
public:
int kthSmallest(TreeNode* root, int k) {
//中序遍历前k个即可
stack<TreeNode* > stack;
while(!stack.empty() || root != nullptr){
while(root != nullptr){
//root非空,入栈
stack.push(root);
root = root->left;
}
//root为空,重定向到栈头
root = stack.top();
stack.pop();
k--;
if(k ==0){
//当k减到0,则该root为我们需要输出的值
return root->val;
}
root = root->right;
}
return 0;
}
};
时间复杂度:O(N),28ms,6.20%
空间复杂度:O(N),23.41MB,19.60%
思路二:如果你需要频繁地查找第k小的值,你将如何优化算法?
记录下每个节点左子树的节点个数。k如果大于左子树的节点个数则一定出现在该节点的右子树中。
199.二叉树的右视图(中等)
给定一个二叉树的根节点root,想象自己站在它的右侧,按照从顶部到底部的顺序,返回从右侧所能看到的节点值。

输入: [1,2,3,null,5,null,4]
输出: [1,3,4]
思路:等价于二叉树的层序遍历(用队列),只返回每一层的最右侧节点的值。
class Solution {
public:
vector<int> rightSideView(TreeNode* root) {
//特判
vector<int> ans;
if(root == nullptr) return ans;
//建立队列辅助实现广度优先遍历
queue<TreeNode* > Q;
Q.push(root);
int sz =1;
while(!Q.empty()){
ans.push_back(Q.back()->val);
sz = Q.size();
while(sz != 0){
root = Q.front();
if(root->left != nullptr) Q.push(root->left);
if(root->right != nullptr) Q.push(root->right);
Q.pop();
sz--;
}
}
return ans;
}
};
时间复杂度:O(N),0ms,100.00%
空间复杂度:O(M),11.84MB,24.62%。M为最大层的节点数。
114.二叉树展开为链表(中等)(仔细领悟)
给你二叉树的根节点root,请你将它展开为一个单链表
- 展开后的单链表应该同样使用TreeNode,其中right子指针指向链表中下一个结点,而左子指针始终为null
- 展开后的单链表应该与二叉树先序遍历顺序相同

输入:root = [1,2,5,3,4,null,6]
输出:[1,null,2,null,3,null,4,null,5,null,6]
思路:使用一个 prev 指针来跟踪先前处理的节点。我们首先处理右子树,然后处理左子树,最后处理根节点。这样,当我们到达根节点时,prev 指针将指向先序遍历中的下一个节点。我们将当前节点的右子节点设置为 prev,并将左子节点设置为 nullptr。然后,我们更新 prev 为当前节点。
class Solution {
public:
TreeNode* prev = nullptr;
void flatten(TreeNode* root) {
//递归终止条件
if (!root) return;
// 先处理右子树,再处理左子树,最后处理根节点
flatten(root->right);
flatten(root->left);
// 扁平化
root->right = prev;
root->left = nullptr;
prev = root;
}
};
105.从前序与中序遍历序列构造二叉树(中等)(不会)
给定两个整数数组preorder和inorder,其中preorder是二叉树的先序遍历,inorder是同一棵树的中序遍历,请构造二叉树并返回其根节点。
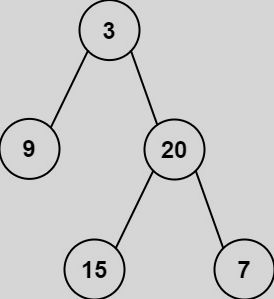
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]
思路:递归实现。中序序列中先找到根节点,根节点左边的一定在左子树,根节点右边的一定在右子树。
只要我们在中序遍历中定位到根节点,那么我们就可以分别知道左子树和右子树中的节点数目。由于同一颗子树的前序遍历和中序遍历的长度显然是相同的,因此我们就可以对应到前序遍历的结果中,对上述形式中的所有左右括号进行定位。
这样以来,我们就知道了左子树的前序遍历和中序遍历结果,以及右子树的前序遍历和中序遍历结果,我们就可以递归地对构造出左子树和右子树,再将这两颗子树接到根节点的左右位置。
class Solution {
private:
unordered_map<int, int> index; //键-表示一个节点的值,值-表示值在中序遍历中出现的位置
public:
TreeNode* myBuildTree(const vector<int>& preorder, const vector<int>& inorder, int preorder_left, int preorder_right, int inorder_left, int inorder_right) {
//该函数用于将中序遍历数组划分为左子树序列、根节点和右子树序列
if (preorder_left > preorder_right) {
return nullptr;
}
// 前序遍历中的第一个节点就是根节点
int preorder_root = preorder_left;
// 在中序遍历中定位根节点
int inorder_root = index[preorder[preorder_root]];
// 先把根节点建立出来
TreeNode* root = new TreeNode(preorder[preorder_root]);
// 得到左子树中的节点数目
int size_left_subtree = inorder_root - inorder_left;
// 递归地构造左子树,并连接到根节点
// 先序遍历中「从 左边界+1 开始的 size_left_subtree」个元素就对应了中序遍历中「从 左边界 开始到 根节点定位-1」的元素
root->left = myBuildTree(preorder, inorder, preorder_left + 1, preorder_left + size_left_subtree, inorder_left, inorder_root - 1);
// 递归地构造右子树,并连接到根节点
// 先序遍历中「从 左边界+1+左子树节点数目 开始到 右边界」的元素就对应了中序遍历中「从 根节点定位+1 到 右边界」的元素
root->right = myBuildTree(preorder, inorder, preorder_left + size_left_subtree + 1, preorder_right, inorder_root + 1, inorder_right);
return root;
}
TreeNode* buildTree(vector<int>& preorder, vector<int>& inorder) {
int n = preorder.size();
// 构造哈希映射,帮助我们快速定位根节点
for (int i = 0; i < n; ++i) {
index[inorder[i]] = i;
}
return myBuildTree(preorder, inorder, 0, n - 1, 0, n - 1);
}
};
时间复杂度:O(1),12ms,90.27%
空间复杂度:O(N),25.44MB,31.59%
437.路径总和(中等)
给定一个二叉树的根节点root,和一个整数targetSum,求该二叉树里节点值之和等于targetSum的路径数目。路径不需要从根节点开始,也不需要在叶子节点结束,但是路径方向必须是向下的(只能从父节点到子节点)。

输入:root = [10,5,-3,3,2,null,11,3,-2,null,1], targetSum = 8
输出:3
解释:和等于 8 的路径有 3 条,如图所示。
思路:递归实现,遍历二叉树,当targetSum-current->val 即为需要在左子树和右子树搜寻的值。
图论(多写)
200.岛屿数量
给你一个由‘1’(陆地)和‘0’(水)组成的二维网格,请你计算网格中岛屿的数量。
岛屿总是被水包围,并且每座岛屿只能由水平方向和/或竖直方向上相邻的陆地连接形成。
此外,你可以假设该网格的四条边均被水包围。
输入:grid = [
[“1”,“1”,“1”,“1”,“0”],
[“1”,“1”,“0”,“1”,“0”],
[“1”,“1”,“0”,“0”,“0”],
[“0”,“0”,“0”,“0”,“0”]
]
输出:1
思路:看力扣官网题解,写得很详细网格的DFS遍历。
class Solution {
public:
int DFS_Islands(vector<vector<char>>& grid,int r,int c){
//该函数用于DFS遍历网格,返回岛屿数量
//终止条件
if(!inLands(grid,r,c)) return 0; //当前节点不在网格内
if(grid[r][c] != '1') return 0; //当前节点不是未访问的陆地
//访问相邻节点
grid[r][c] = '2'; //将当前节点标记为已访问
DFS_Islands(grid,r-1,c);
DFS_Islands(grid,r+1,c);
DFS_Islands(grid,r,c-1);
DFS_Islands(grid,r,c+1);
return 1;
}
bool inLands(vector<vector<char>>& grid,int r,int c){
//该函数用于判断当前节点是否位于网格内
return r>=0 && c>=0 && r<grid.size() && c<grid[0].size();
}
int numIslands(vector<vector<char>>& grid) {
int number = 0;
for(int r=0; r<grid.size(); r++){
for(int c=0; c<grid[0].size();c++){
//遍历网格
if(grid[r][c] =='1') number = number+DFS_Islands(grid,r,c);
}
}
return number;
}
};
时间复杂度:O(r*c),20ms,99.83%
空间复杂度:O(N),11.94MB,64.18%。递归实现,内部有栈
例题1,695.最大岛屿面积(中等)
给定一个包含了一些0和1的非空二维数组grid,一个岛屿是一组相邻的1(代表陆地),这里的【相邻】要求两个1必须在水平或者竖直方向上相邻。你可以假设grid的四个边缘都被0(代表海洋)包围着。
找到给定的二维数组中最大的岛屿面积。如果没有岛屿,则返回面积为0。

输入:grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
输出:6
解释:答案不应该是 11 ,因为岛屿只能包含水平或垂直这四个方向上的 1 。
class Solution {
public:
int DFS_Area(vector<vector<int> >&grid, int r, int c ){
//该函数用于网格的深度优先遍历,并计算岛屿面积
//终止条件
if (!inArea(grid,r,c)){
return 0;
}
//如果当前节点不是未访问的岛屿,直接返回
if(grid[r][c]!=1) return 0;
grid[r][c] = 2; //将当前节点标记为已访问
//访问上下左右四个相邻节点
return 1
+DFS_Area(grid,r-1,c)
+DFS_Area(grid,r+1,c)
+DFS_Area(grid,r,c-1)
+DFS_Area(grid,r,c+1);
}
bool inArea(vector<vector<int> > &grid,int r, int c){
//该函数用于判断当前节点是否位于网格内
return r>=0 && c >=0 && r<grid.size() && c<grid[0].size();
}
int maxAreaOfIsland(vector<vector<int>>& grid) {
int res = 0;
for(int r=0;r<grid.size();r++){
for(int c=0;c<grid[0].size();c++){
if(grid[r][c]==1){//对于岛屿进行访问
int a = DFS_Area(grid,r,c);
res = max(res,a);
}
}
}
return res;
}
};
时间复杂度:O(r*c),12ms,94.97%
空间复杂度:O(N),22.42MB,67.04%。递归实现
例题2,827 填海造陆问题(难)
在二维地图上,0代表海洋,1代表陆地,我们最多只能将一格0(海洋)变成1(陆地)。进行填海之后,地图上最大的岛屿面积是多少?
例题3,463 岛屿的周长(简单)
给定一个包含 0 和 1 的二维网格地图,其中 1 表示陆地,0 表示海洋。网格中的格子水平和垂直方向相连(对角线方向不相连)。整个网格被水完全包围,但其中恰好有一个岛屿(一个或多个表示陆地的格子相连组成岛屿)。
岛屿中没有“湖”(“湖” 指水域在岛屿内部且不和岛屿周围的水相连)。格子是边长为 1 的正方形。计算这个岛屿的周长。

输入:grid = [[0,1,0,0],[1,1,1,0],[0,1,0,0],[1,1,0,0]]
输出:16
解释:它的周长是上面图片中的 16 个黄色的边

当我们的 dfs 函数因为「坐标 (r, c) 超出网格范围」返回的时候,实际上就经过了一条黄色的边;而当函数因为「当前格子是海洋格子」返回的时候,实际上就经过了一条蓝色的边。这样,我们就把岛屿的周长跟 DFS 遍历联系起来了,我们的题解代码也呼之欲出:
class Solution {
public:
int DFS_island(vector<vector<int>>& grid,int r,int c){
//该函数用于DFS遍历网格,返回周长
//终止条件
if(!inGrid(grid,r,c)) return 1; //超出网格边界
if(grid[r][c] == 0) return 1; //当前节点是海洋
if(grid[r][c] == 2) return 0; //当前节点已访问
//访问相邻节点
grid[r][c] = 2; //标记为已访问
return DFS_island(grid,r-1,c)+DFS_island(grid,r+1,c)+DFS_island(grid,r,c-1)+DFS_island(grid,r,c+1);
}
bool inGrid(vector<vector<int>>& grid, int r,int c){
//该函数用于判断当前节点是否在网格内
return r>=0 && c>=0 && r<grid.size() && c<grid[0].size();
}
int islandPerimeter(vector<vector<int>>& grid) {
for(int r=0; r<grid.size();r++){
for(int c=0; c<grid[0].size();c++){
if(grid[r][c] == 1) return DFS_island(grid,r,c);
}
}
return 0;
}
};
时间复杂度:O(r*c),112ms,23.4%
空间复杂度:O(N),92.35MB,24.18%
994.腐败的橘子(中等)
在给定的M*N网格grid中,每个单元格可以有以下三个值之一:
- 值0代表空单元格
- 值1代表新鲜橘子
- 值2代表腐烂的橘子
- 每分钟,腐烂的橘子周围4个方向上相邻的新鲜橘子都会腐烂。
- 返回直到单元格中没有新鲜橘子为止所必须经过的最小分钟数。如果不可能,返回-1。

输入:grid = [[2,1,1],[1,1,0],[0,1,1]]
输出:4
思路:广度优先搜索的过程。
力扣官方题解:多源广度优先搜索
class Solution {
public:
int orangesRotting(vector<vector<int>>& grid) {
int row=grid.size();
int col=grid[0].size();
int res=0;
vector<int>dx={-1,0,0,1};//辅助定位即将被腐烂的橘子的横坐标
vector<int>dy={0,1,-1,0};//辅助定位即将被腐烂的橘子的纵坐标,对应构成腐烂橘子的四个污染方向
queue<pair<int,int>>rot ; //pair存储一对关联的数据
for(int i=0;i<row;++i) //将腐烂橘子一一压入队列
for(int j=0;j<col;++j)
if(grid[i][j]==2)
rot.push({i,j}); //将腐烂橘子的坐标压入队列
while(!rot.empty())
{
int vol=rot.size();//标记队列内腐烂橘子个数
for(int i=0;i<vol;++i)
{
pair<int,int> fir=rot.front();//取出首个腐烂橘子
rot.pop();
for(int j=0;j<4;++j)//进行四个方向污染
{
int x=fir.first+dx[j],y=fir.second+dy[j];
if(x>=0&&x<row&&y>=0&&y<col&&grid[x][y]==1)//判断是否存在新鲜橘子
{
grid[x][y]=2;
rot.push({x,y});
}
}
}
if(!rot.empty())//如果为空表示一开始就没有腐烂橘子,返回0分钟
res++;//每次取出队列所有橘子时间加1,同时压入被污染的新一批橘子
}
for(int i=0;i<row;++i)//检查是否还有新鲜橘子
for(int j=0;j<col;++j)
if(grid[i][j]==1)
return -1;
return res;
}
};
时间复杂度:4ms,91.51%
空间复杂度:12.74MB,45.45%
自写:
class Solution {
public:
int orangesRotting(vector<vector<int>>& grid) {
//该函数利用多源BFS返回腐烂橘子所需天数
//遍历网格找出第0天,所有的烂橘子,作为第一天入队列的开始
int m = grid.size();
int n = grid[0].size();
int flush = 0;
queue<pair<int, int>> rot; //队列存储烂橘子的坐标
for(int r=0; r<m;r++){
for(int c=0; c<n; c++){
//遍历网格
if(grid[r][c]==2) rot.push({r,c}); //将烂橘子坐标存入队列
if(grid[r][c]==1) flush++; //记录好橘子的个数
}
}
//BFS污染周围橘子
int day = 0;
while(!rot.empty() && flush >0){
day++;
int vol = rot.size(); //每层烂橘子的个数,即循环的次数
for (int i=0; i<vol;i++){
//循环vol次,将该层橘子依次取出
pair<int,int> fir = rot.front();
rot.pop();
//将fir指向的烂橘子向四个方向污染
int r=fir.first;
int c=fir.second;
if((r-1)>=0 && grid[r-1][c] == 1) {
grid[r-1][c] = 2;
rot.push({r-1,c});
flush--;
}
if((r+1)<m && grid[r+1][c] == 1) {
grid[r+1][c] = 2;
rot.push({r+1,c});
flush--;
}
if((c-1)>=0 && grid[r][c-1] == 1) {
grid[r][c-1] = 2;
rot.push({r,c-1});
flush--;
}
if((c+1)<n && grid[r][c+1] == 1) {
grid[r][c+1] = 2;
rot.push({r,c+1});
flush--;
}
}
}
if(flush == 0) return day;
else return -1;
}
};
时间复杂度:O(MN),8ms,64.00%
空间复杂度:O(MN),12.8MB,37.24%
207.课程表(中等)
你这个学期必须选修numCourses门课程,记为0到numCourses-1。
在选修某些课程之前需要一些先修课程。先修课程按数组prerequisite给出,其中prerequisite【i】=【ai,bi】,表示如果要学习课程ai则必须先学习课程bi。
例如,先修课程对【0,1】表示:想要学习课程0,你需要先完成课程1。
请你判断是否可能完成所有课程的学习?如果可以,返回true;否则,返回false。
示例 1:
输入:numCourses = 2, prerequisites = [[1,0]]
输出:true
解释:总共有 2 门课程。学习课程 1 之前,你需要完成课程 0 。这是可能的。
示例 2:
输入:numCourses = 2, prerequisites = [[1,0],[0,1]]
输出:false
解释:总共有 2 门课程。学习课程 1 之前,你需要先完成课程 0 ;并且学习课程 0 之前,你还应先完成课程 1 。这是不可能的。
思路:拓扑排序问题用广度优先遍历实现
对于图G中的任意一条有向边(u,v),u在排列中都出现在v的前面。
那么称该排列是图G的【拓扑排序】。
总结:拓扑排序问题
- 根据依赖关系,构建邻接表、入度数组。
- 选取入度为 0 的数据,根据邻接表,减小依赖它的数据的入度。
- 找出入度变为 0 的数据,重复第 2 步。
- 直至所有数据的入度为 0,得到排序,如果还有数据的入度不为 0,说明图中存在环。
拓扑排序的图解,依层将入度为0的节点从图中删除。如果能删除所有节点,则存在拓扑排序。如果不能,则不存在拓扑排序,一定存在回路。
class Solution {
public:
bool canFinish(int numCourses, vector<vector<int>>& prerequisites) {
//该函数用来判断是否存在拓扑排序
vector<int> edges(numCourses); //用以记录每个节点的入度
unordered_map<int,vector<int> > map; //哈希表用来存储邻接链表
//遍历prerequisite,构造邻接表和入度数组
for(int i=0;i<prerequisites.size();i++){
map[prerequisites[i][1]].push_back(prerequisites[i][0]);
edges[prerequisites[i][0]]++;
}
//BFS遍历,将入度为0的节点作为第一层,再将第一层全部出队列,并同时压入第二层
queue<int> node;
for(int i=0; i<edges.size();i++){
if(edges[i]==0) node.push(i); //将入度为0的节点放入队列
}
int cnt=0; //用以记录已经处理的节点数
while(!node.empty()){
int ptr = node.front();
node.pop();
cnt++;
//更新邻接表和入度数组,从链表中删除ptr节点,将ptr指向节点的邻接节点入度为0的节点全部入队列
for(int i=0;i<map[ptr].size();i++){
if(edges[map[ptr][i]]>0){
edges[map[ptr][i]]--;
if(edges[map[ptr][i]]==0){
node.push(map[ptr][i]);//将入度减为0的节点入队列
}
}
}
}
//如果最后还有节点没有入过队列,则说明不存在拓扑排序
if(cnt == numCourses) return true;
else return false;
}
};
时间复杂度:O(M+N),20ms,66.55%
空间复杂度:O(M+N),13.62MB,27.41%
208.实现Trie(前缀树) (中等)
前缀树是一种树形数据结构,用于高效地存储和检索字符串数据集中的键。这一数据结构有相当多的应用场景,例如自动补完和拼写检查。
实现Trie类:
- Trie()初始化前缀树对象
- void insert(string word)向前缀树中插入字符串word。
- boolean search(String word)如果字符串word在前缀树中,返回true(即,在检索之前已经插入);否则,返回false。
- boolean starsWith(String prefix)如果之前已经插入的字符串word的前缀之一为prefix,返回true;否则,返回false。
示例:
输入
[“Trie”, “insert”, “search”, “search”, “startsWith”, “insert”, “search”]
[[], [“apple”], [“apple”], [“app”], [“app”], [“app”], [“app”]]
输出
[null, null, true, false, true, null, true]
解释
Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”); // 返回 True
trie.search(“app”); // 返回 False
trie.startsWith(“app”); // 返回 True
trie.insert(“app”);
trie.search(“app”); // 返回 True
