机器人正运动学(2)—— 自由度
目录
-
- 1. 自由度的定义
- 2. 自由度的计算
-
- 2.1 刚体的自由度
- 2.2 运动副
- 2.3 自由度算例
- 3. 总结
1. 自由度的定义
自由度在很多领域中会出现,对于机器人而言,我们这里谈的也就是机构的自由度。任何一台机器人都可以认为是一个机构。所谓自由度通俗的讲就是为了唯一确定一个机构的运动状态所必须的独立变量的个数。
在自由度的定义中,唯一、必须、独立是三个比较关键的词。唯一确定即给定这些变量后机器人具有唯一的位型;必须则是一种最少的概念,也就是能够确定机器人状态的最少的变量数;独立则表示这些变量可以独立的变化。
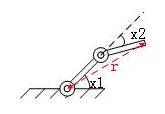
很明显为了确定这个二连杆机器人的运动所需的独立变量个数为2。图中的角度x1和x2就是为了确定二连杆机器人当前状态的一组独立变量。当然这种独立变量并不唯一,我们同样可以选择角度x1和始末两端连线长度r来描述机器人当前状态。在分析力学中这组独立变量又被称为广义坐标,这个概念我们暂时不提,后面会有涉及。
2. 自由度的计算
2.1 刚体的自由度
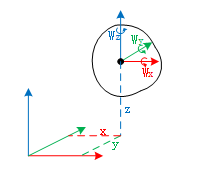
在给出具体的公式之前,我们首先考虑,一个不受任何约束的刚体在空间中的自由度,很显然应该是6。因为刚体可以沿着x,y,z三个坐标轴方向平移,也可以绕着x,y,z三个轴旋转。因此为了确定一个不受约束的刚体的运动状态,我们需要六个独立的变量。如下面的图所示。x,y,z可以唯一确定刚体上的一个点,但是只有这三个变量,刚体依然可以绕该点做任意的旋转运动,因此还需要Wx,Wy,Wz三个姿态变量来确定刚体的姿态,这也就是刚体的定位和定姿。
机器人通常是由连杆构成,我们通常将每一个连杆看作一个刚体,因此不考虑连杆之间的连接时,机器人每个连杆都有6个自由度。对于一个有n个连杆的机器人,如果不考虑连杆约束那么它的自由度是6n。
2.2 运动副
机器人连杆之间的相互连接引入了约束。在机构学上将这种约束称为运动副。运动副是指两个构件既保持接触又有相对运动的活动连接。下图是一些比较常见的运动副。

移动副是一种使两个构件发生相对移动的连接结构,它具有一个移动自由度,约束了刚体其他5个运动。(只能沿某一个轴平移,缺少三个旋转自由度和两个平移自由度);
转动副是一种使两个构件发生相对转动的连接结构,它具有一个转动自由度,约束了刚体的其他5个运动。
圆柱副是一种使两个构件发生同轴转动和移动的连接结构,通常由共轴的转动副和移动副组合而成。它具有两个独立的自由度,约束了刚体的其他4个运动。
2.3 自由度算例
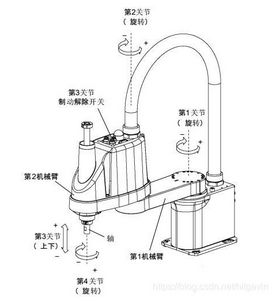
机器人的第一和第二关节为旋转关节,第三关节为移动关节,第四关节为旋转关节。这样一个机器人自由度如何计算呢。
首先第一个连杆是基座,由于基座固定,因此其自由度为0;
第二个连杆通过转动副与第一个连杆相连,转动副引入五个约束。
第三个连杆通过转动副连接到第二个连杆,同样引入五个约束。
第四个连杆通过滚珠丝杆花件连接到第三个连杆,滚珠丝杠有两个自由度,可以认为是一个圆柱副,这个连接引入了四个约束。
而机器人总共有四个连杆,那么总的连杆自由度数为4*6=24;总的约束为6+5+5+4=20。因此机器人的自由度为4。
2.4 自由度计算公式
因此总的来说,自由度计算公式如下: F = 6 ⋅ n − ∑ i = 1 g p i F= 6\cdot n-\sum_{i=1}^{g} p_{i} F=6⋅n−i=1∑gpi
其中,n代表连杆数量,6代表我们探讨问题的空间的维度,通常为3维的平面空间或者6维的立体空间,g为运动副的个数,pi代表第i个运动副所带来的约束的个数。
当然关于自由度有许多更为艰深的话题,这绝对不是上面这个简简单单的公式能够完全探讨清楚的,实际上上面的公式并不能计算所有机构的自由度。在现代通常利用拓扑学,李群等更复杂的数学来诠释自由度。
但是对于机器人学而言,我们能够理解到当前这个程度已基本够用。有时我们甚至可以认为驱动器的个数就是机器人的自由度。
3. 总结
关于自由度就先介绍到这里,之后将介绍坐标系变换,这是整个机器人学的根基。由于个人能力有限,所述内容难免存在疏漏,欢迎指出,欢迎讨论。
下一篇:机器人正运动学(3)—— 坐标系及其变换
————————————————
版权声明:本文为CSDN博主「hitgavin」的原创文章,遵循CC 4.0 BY-SA版权协议,转载请附上原文出处链接及本声明。
原文链接:https://blog.csdn.net/hitgavin/article/details/100569001