dp入门题 笔记
文章目录
- DP笔记
-
-
- 最长回文子串:
- 最长回文子序列:
- 最佳观光组合:
- 最大正方形
- 丑数
- 解码方法
- 不同的二叉搜索树
- 路径问题
-
- 不同路径
- 最小路径
- 股票买卖题型
-
- 买卖股票最佳时机
- 当进行限制交易次数:
- 含有冷冻期的买卖股票时机:
- 背包问题
-
-
- 单词拆分(**存在性问题**)
- 零钱兑换:
- 整数划分
- 经典背包问题(题解暂未写全)
-
- 单调栈类型
-
- 接雨水
-
- 1.单调栈
- 2.dp
- 最长上升子序列
- 状态压缩
- 最短编辑距离
- 记忆化搜索
- 树形DP (过两天更新)
- 数位DP
-
- 计数问题
-
- 思路:
-
DP笔记
最长回文子串:
**中心扩散 **: 从中段进行两边扩散 定义 l,r 两个指针分别向左右两边进行移动
分三种情况 :
1) arr[i] == arr[l] : l 向左端进行遍历 count ++
2) arr[r] == arr[i] : r 向右端进行遍历 count ++
3)arr[l ] == arr[r] : l 、r 分别向左和右进行遍历 count+=2
public String longestPalindrome(String s) {
if(s.length()<=1){
return s;
}
char[] arr = s.toCharArray();
String ans = String.valueOf(arr[0]);
int max = 1 ;
for(int i =0;i=0&&arr[i]==arr[l]) { // 情况1
l--;
count++;
}
while(r=0&&arr[l]==arr[r]) {// 情况3
r++;
l--;
count+=2;
}
if(count>max) {
max = count;
ans = s.substring(l+1,r);
}
}
return ans;
}
最长回文子序列:
分析: 由于需要得到最长的回文子序 , 定义两个指针 分别进行遍历 。 i 进行 对 字符串遍历 , j 进行查找最长的字串。
当 arr[ i ] != arr [ j ] :
f[i] [j] = max(f[ i-1 ] [ j ] , f[ i ] [ j -1 ] )
选取上一个状态 i -1 或者 j -1 的位置进行取最大值 表示 从 i - j 段 的 回文字符子串 最大值。
当 arr[ i ] == arr [ j ] :
f[i] [j] = f[i-1] [j -1] + 2
代码如下:
public int longestPalindromeSubseq(String s) {
int n = s.length();
char[] arr = s.toCharArray();
int[][] f = new int[n+1][n+1];
for(int i = n-1 ; i >= 0 ; --i){
f[i][i] = 1;
for(int j = i+1 ; j<n; ++j){
if(arr[i] == arr[j]){
f[i][j] = f[i+1][j-1] + 2;
}else{
f[i][j] = Math.max(f[i+1][j],Math.max(f[i][j-1],f[i][j]));
}
}
}
return f[0][n-1];
}
最佳观光组合:
分析:
将得分公式进行拆分:
a n s = v a l u e s [ i ] + i + v a l u e s [ j ] − j ans = values[i] + i + values[j] - j ans=values[i]+i+values[j]−j
相当于 在 j 前 查找 values[i] + i 的 最大值 max 对 max + values[j] - j 进行动态规划
public int maxScoreSightseeingPair(int[] values) {
// ans = values[i] + i + values[j] - j
// 相当于 在 j 前 查找 values[i] + i 的 最大值 max 对 max + values[j] - j 进行动态规划
int ans = 0 ;
int max = values[0] + 0;
for(int j= 1 ; j < values.length; j++){
ans = Math.max(ans,max + values[j]-j);
max = Math.max(max,values[j]+j);
}
return ans;
}
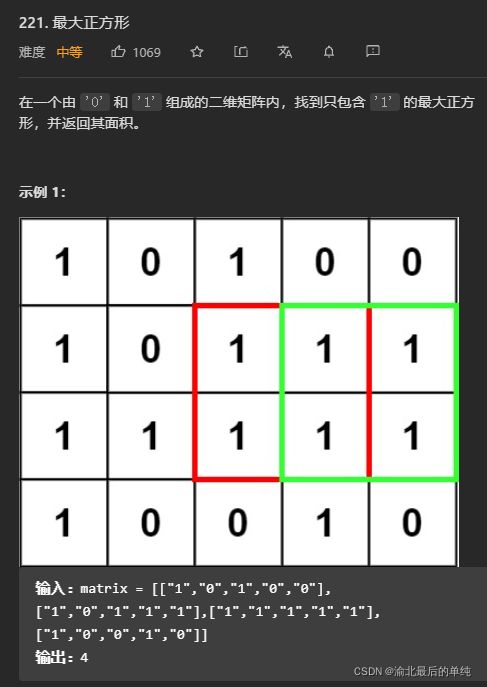
最大正方形
public int maximalSquare(char[][] matrix) {
int max = 0 ;
int n = matrix.length;
int m = matrix[0].length;
if (matrix == null || matrix.length == 0 || matrix[0].length == 0) {
return max;
}
int[][] f= new int[n][m];
for(int i = 0 ; i < n ; ++i ) {
for(int j = 0 ; j < m ; ++j) {
if(matrix[i][j]=='1') {
if(i == 0 || j == 0) {
f[i][j] = 1;
}else {
f[i][j] = Math.min(Math.min(f[i - 1][j], f[i][j - 1]), f[i - 1][j - 1])+1;
}
max = Math.max(max, f[i][j]);
}
}
}
return max*max;
}
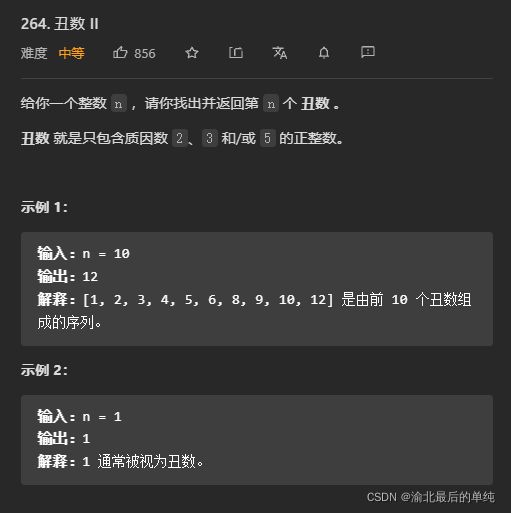
丑数
public int nthUglyNumber(int n) {
int p2 = 1 , p3 = 1 , p5 =1 ;
int[] f = new int[n+1];
f[1] = 1;
for(int i = 2;i<=n ; ++i) {
int num2 = f[p2]*2;
int num3 = f[p3]*3;
int num5 = f[p5]*5;
f[i] = Math.min(Math.min(num2, num3),num5);
if(num2 == f[i]) {
p2++;
}
if(num3 == f[i]) {
p3++;
}
if(num5 == f[i]) {
p5++;
}
}
return f[n];
}
解码方法
public int numDecodings(String s) {
int n = s.length();
// a = f[i-2], b = f[i-1], c=f[i]
int a = 0, b = 1, c = 0;
for (int i = 1; i <= n; ++i) {
c = 0;
if (s.charAt(i - 1) != '0') {
c += b;
}
if (i > 1 && s.charAt(i - 2) != '0' && ((s.charAt(i - 2) - '0') * 10 + (s.charAt(i - 1) - '0') <= 26)) {
c += a;
}
a = b;
b = c;
}
return c;
}
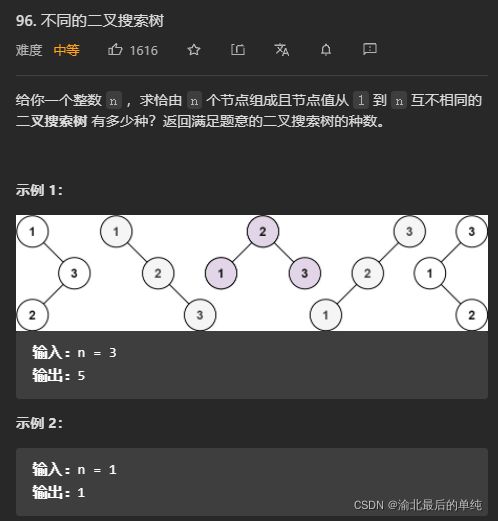
不同的二叉搜索树
-
标签:动态规划
-
假设 n 个节点存在二叉排序树的个数是 G (n),令 f(i) 为以 i 为根的二叉搜索树的个数,则
G ( n ) = f ( 1 ) + f ( 2 ) + f ( 3 ) + f ( 4 ) + . . . + f ( n ) G(n)=f(1)+f(2)+f(3)+f(4)+...+f(n) G(n)=f(1)+f(2)+f(3)+f(4)+...+f(n)- 当 i 为根节点时,其左子树节点个数为 i-1 个,右子树节点为 n-i,则
f ( i ) = G ( i − 1 ) ∗ G ( n − i ) f(i)=G(i−1)∗G(n−i) f(i)=G(i−1)∗G(n−i)
- 当 i 为根节点时,其左子树节点个数为 i-1 个,右子树节点为 n-i,则
-
综合两个公式可以得到 卡特兰数 公式
G ( n ) = G ( 0 ) ∗ G ( n − 1 ) + G ( 1 ) ∗ ( n − 2 ) + . . . + G ( n − 1 ) ∗ G ( 0 ) G(n)=G(0)∗G(n−1)+G(1)∗(n−2)+...+G(n−1)∗G(0) G(n)=G(0)∗G(n−1)+G(1)∗(n−2)+...+G(n−1)∗G(0)
public int numTrees(int n) {
int[] dp = new int[n+1];
dp[0] = 1;
dp[1] = 1;
for(int i = 2; i < n + 1; i++)
for(int j = 1; j < i + 1; j++)
dp[i] += dp[j-1] * dp[i-j];
return dp[n];
}
路径问题
不同路径
public int uniquePathsWithObstacles(int[][] obstacleGrid) {
if (obstacleGrid == null || obstacleGrid.length == 0) {
return 0;
}
int[][] ans = new int[obstacleGrid.length][obstacleGrid[0].length];
ans[0][0] = 0;
int m = obstacleGrid.length, n = obstacleGrid[0].length;
for (int i = 0; i < m && obstacleGrid[i][0] == 0; i++) {
ans[i][0] = 1;
}
for (int j = 0; j < n && obstacleGrid[0][j] == 0; j++) {
ans[0][j] = 1;
}
for(int i = 1 ; i < obstacleGrid.length ; ++i) {
for(int j = 1; j < obstacleGrid[0].length ;++j) {
if(obstacleGrid[i][j]!=1)ans[i][j] = ans[i-1][j] + ans[i][j-1];
}
}
return ans[obstacleGrid.length-1][obstacleGrid[0].length-1];
}
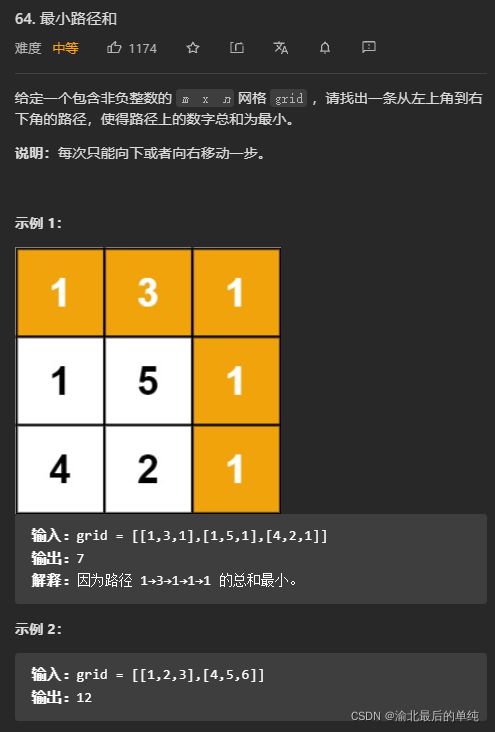
最小路径
public int minPathSum(int[][] grid) {
int m = grid.length;
int n = grid[0].length;
if(m==0||n==0){ return 0;}
int[][] f = new int[m+1][n+1];
for(int i = 1; i <= m ; i++) {
f[i][1] = f[i-1][1] + grid[i-1][0];
}
for(int i = 1; i <= n ; i++) {
f[1][i] = f[1][i-1] + grid[0][i-1];
}
for(int i = 2 ; i <= m ; i++) {
for(int j = 2 ; j<= n;j++) {
f[i][j] = Math.min(f[i][j-1], f[i-1][j])+grid[i-1][j-1];
}
}
return f[m][n];
}
股票买卖题型
买卖股票最佳时机
第一题贪心算法应该快很多 就 不讲 。 此类问题 思路大致一致
第二题也可用贪心做 ans =max(ans, ans+prices[i]-prices[i-1]);
分析: 共有两个属性值 , 未持有 和持有股票
定义 f[ i ] [ 2 ] f[ i ] [ 0 ]表示 第i 天 的未持有股票的最大收益 。 分为 卖股票 和 保持之前状态 ,所以
f [ i ] [ 0 ] = m a x ( f [ i − 1 ] [ 0 ] , f [ i − 1 ] [ 1 ] + p r i c e s [ i ] ) f[i][0] = max(f[i-1][0],f[i-1][1]+prices[i]) f[i][0]=max(f[i−1][0],f[i−1][1]+prices[i])
f[ i ] [ 1 ] 表示第 i 天 的 持有股票的最大收益。 分为购买股票和继续持有之前的股票,所以
f [ i ] [ 1 ] = m a x ( f [ i − 1 ] [ 1 ] , f [ i − 1 ] [ 0 ] − p r i c e s [ i ] ) f[i][1] = max(f[i-1][1],f[i-1][0]-prices[i]) f[i][1]=max(f[i−1][1],f[i−1][0]−prices[i])
public int maxProfit(int[] prices) {
int n = prices.length;
if(n < 2 ) return 0;
int f[][]= new int[n+1][2];
f[0][0] = 0;
f[0][1] = -prices[0];
for(int i =1 ; i < n ; ++i){
f[i][0] = Math.max(f[i-1][0],f[i-1][1]+prices[i]);
f[i][1] = Math.max(f[i-1][1],f[i-1][0]-prices[i]);
}
return f[n-1][0];
}
优化: 发现 f[i] [0] || f[i] [1] 仅和前一天的 状态有关,因此用滚动数组进行优化
定义一个最小花费ans[1] 替代 f[ i ] [ 1 ] , ans[0] 替代f[ i ] [ 0 ]
public int maxProfit(int[] prices) {
int n = prices.length;
int f[]= new int[2];
f[0] = 0;
f[1] = -prices[0];
for(int i = 1 ; i < n ; ++i){
f[0] = Math.max(f[0],f[1]+prices[i]);
f[1] = Math.max(f[1],f[0]-prices[i]);
}
return f[0];
}
当进行限制交易次数:
沿用之前分析思路:
再增加一个维度第k次交易 即:f[ i ] [ 0|1 ] [ 0 | 1 ]
状态转移方程:
第一次交易未持有股票时最大收益:
f [ i ] [ 0 ] [ 0 ] = m a x ( f [ i − 1 ] [ 0 ] [ 0 ] , f [ i − 1 ] [ 1 ] [ 0 ] + p r i c e s [ i ] ) f[i][0][0] = max(f[i-1][0][0] , f[i-1][1][0]+prices[i]) f[i][0][0]=max(f[i−1][0][0],f[i−1][1][0]+prices[i])
第一次交易持有股票时最大收益(因为第一笔交易和第二笔交易不能同时进行,所以只需要记录第一次交易的购买最小值 在进行计算收益即可):
f [ i ] [ 1 ] [ 0 ] = m a x ( f [ i − 1 ] [ 1 ] [ 0 ] , − p r i c e s [ i ] ) f[i][1][0] = max(f[i-1][1][0],-prices[i]) f[i][1][0]=max(f[i−1][1][0],−prices[i])
第二次交易未持有股票时最大收益:
f [ i ] [ 0 ] [ 1 ] = m a x ( f [ i − 1 ] [ 0 ] [ 1 ] , f [ i − 1 ] [ 1 ] [ 1 ] + p r i c e s [ i ] ) f[i][0][1] = max(f[i-1][0][1],f[i-1][1][1]+prices[i]) f[i][0][1]=max(f[i−1][0][1],f[i−1][1][1]+prices[i])
第一次交易持有股票时最大收益:
f [ i ] [ 1 ] [ 1 ] = m a x ( f [ i − 1 ] [ 1 ] [ 1 ] , f [ i − 1 ] [ 0 ] [ 0 ] − p r i c e s [ i ] ) f[i][1][1] = max(f[i-1][1][1],f[i-1][0][0]-prices[i]) f[i][1][1]=max(f[i−1][1][1],f[i−1][0][0]−prices[i])
public int maxProfit(int[] prices) {
int n = prices.length;
int[][][] f = new int[n][2][2];
f[0][1][0] = -prices[0];
f[0][1][1] = -prices[0];
for (int i = 1; i < n; ++i) {
f[i][0][0] = Math.max(f[i-1][0][0],f[i-1][1][0]+prices[i]);
f[i][1][0] = Math.max(f[i-1][1][0],-prices[i]);
f[i][0][1] = Math.max(f[i-1][0][1],f[i-1][1][1]+prices[i]);
f[i][1][1] = Math.max(f[i-1][1][1],f[i-1][0][0]-prices[i]);
}
return f[n-1][0][1];
}
优化: 可以发现第i天的状态只与第i-1天的状态有关,因此可以考虑使用滚动数组进行优化空间
public int maxProfit(int[] prices) {
int n = prices.length;
int buy1 = -prices[0], sell1 = 0; // 第一次交易
int buy2 = -prices[0], sell2 = 0; // 第二次交易
for (int i = 1; i < n; ++i) {
buy1 = Math.max(buy1, -prices[i]);
sell1 = Math.max(sell1, buy1 + prices[i]);
buy2 = Math.max(buy2, sell1 - prices[i]);
sell2 = Math.max(sell2, buy2 + prices[i]);
}
return sell2;
}
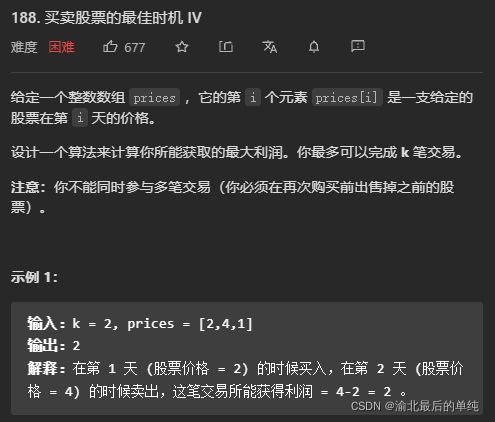
分析: 与第三题相似,只不过再将交易维度从2变成了k维;
以下直接给出优化后的代码:
public int maxProfit(int k, int[] prices) {
if(prices.length == 0 || k == 0) return 0;
int dp[] = new int[k*2];
for(int i = 0 ; i < 2*k ;i+=2){
dp[i] = 0;
dp[i+1] = -prices[0];
}
// 每一次的 持有股票定义为 m%2== 1 , 未持有则为 m%2==0
for(int i = 1; i < prices.length;++i){
dp[0] = Math.max(dp[0],dp[1]+prices[i]); // 第一次出售的收益
dp[1] =Math.max(dp[1],-prices[i]); // 第一次持有所花的钱
for(int j = 2 ; j < 2*k ;j+=2){
dp[j] = Math.max(dp[j],dp[j+1]+prices[i]); // 第j次出售的收益
dp[j+1] =Math.max(dp[j+1],dp[j-2]-prices[i]);// 持有第j次的股票
}
}
return dp[2*k-2];
}
含有冷冻期的买卖股票时机:
分析:状态转移方程
未持有股票:
f [ i ] [ 0 ] = m a x ( f [ i − 1 ] [ 2 ] , f [ i − 1 ] [ 0 ] ) f[i][0] = max(f[i-1][2],f[i-1][0]) f[i][0]=max(f[i−1][2],f[i−1][0])
持有股票:
f [ i ] [ 1 ] = m a x ( f [ i − 1 ] [ 1 ] , f [ i − 1 ] [ 0 ] − p r i c e s [ i ] ) f[i][1] = max(f[i-1][1],f[i-1][0]-prices[i]) f[i][1]=max(f[i−1][1],f[i−1][0]−prices[i])
冷冻期:
f [ i ] [ 2 ] = f [ i − 1 ] [ 0 ] + p r i c e s [ i ] f[i][2] = f[i-1][0]+prices[i] f[i][2]=f[i−1][0]+prices[i]
public int maxProfit(int[] prices) {
if (prices.length == 0) {
return 0;
}
int n = prices.length;
int[][] f = new int[n][3];
f[0][1] = -prices[0];
for (int i = 1; i < n; ++i) {
f[i][0] = Math.max(f[i-1][2],f[i-1][0]);
f[i][1] = Math.max(f[i-1][1],f[i-1][0]-prices[i]);
f[i][2] = f[i-1][1]+prices[i];
}
return Math.max(f[n - 1][0], f[n - 1][2]);
}
**优化:思路与前几题相似 **是用滚动数组进行空间优化
public int maxProfit(int[] prices) {
if(prices.length==0) return 0;
int f1, f2 ,f3 , f4, f5, f6; // f1 f6 :未持有 f2 f4: 冷冻期 f3 f5: 持有
f1 = 0;
f2 = 0;
f3 = -prices[0];
for(int i = 1; i < prices.length;++i){
f4 = f3+prices[i];// -1 0 -1 2 0 2 4
f5 = Math.max(f1-prices[i],f3);
f6 = Math.max(f2,f1);
f2 = f4;
f1 = f6;
f3 = f5;
}
return Math.max(f1,f2);
}
背包问题
单词拆分(存在性问题)
方法一:
public class Solution {
public boolean wordBreak(String s, List<String> wordDict) {
Set<String> wordDictSet = new HashSet(wordDict);
boolean[] dp = new boolean[s.length() + 1];
dp[0] = true;
for (int i = 1; i <= s.length(); i++) {
for (int j = 0; j < i; j++) {
if (dp[j] && wordDictSet.contains(s.substring(j, i))) {
dp[i] = true;
break;
}
}
}
return dp[s.length()];
}
}
方法二:
类似于背包问题 , 通过组装单词进行 dp
d p [ i ] = d p [ i ] ∣ ∣ d p [ i − l e n ] dp[i] = dp[i] || dp[i-len] dp[i]=dp[i]∣∣dp[i−len]
public boolean wordBreak(String s, List<String> wordDict) {
boolean dp[] = new boolean[s.length() + 1];
dp[0] = true;
for(int i = 1; i <= s.length() ; ++i){
for(String k : wordDict){
int len = k.length();
if(i-len>=0 && s.substring(i-len,i).equals(k)){
dp[i] = dp[i] || dp[i-len];
}
}
}
return dp[s.length()];
// dp[i] = dp[i] || dp[i-len]
}
零钱兑换:
类似于01背包问题,直接在面额内进行最小值计算。
属性:count 状态
特征: 面额
状态转移方程:
f [ i ] = m i n ( f [ i ] , f [ i − c o i n s [ i ] ] + 1 ) f[i] = min(f[i],f[i-coins[i]]+1) f[i]=min(f[i],f[i−coins[i]]+1)
public int coinChange(int[] coins, int amount) {
if(coins.length == 0){
return
}
int[] f = new int[amount+1];
Arrays.fill(f, 1000000);
f[0] = 0;
for(int i = 0; i < coins.length ; ++i){
for(int j = coins[i] ; j <= amount ; ++j){
f[j] = Math.min(f[j] , f[j-coins[i]]+1);
}
}
return f[amount];
}
整数划分
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
public static void main(String args[]) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
int n ;
n = sc.nextInt();
int[]f = new int[n+1];
f[0] = 1;
for(int i = 1; i <= n ; ++i){
for(int j = i ; j <= n ; j++){
f[j] = f[j]+f[j-i];
f[j] %= 1000000007;
}
}
System.out.print(f[n]);
}
}
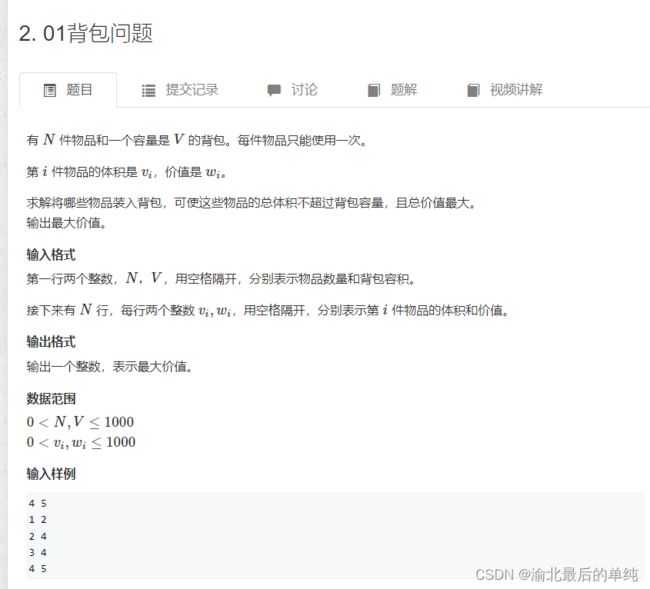
经典背包问题(题解暂未写全)
public static void package01() {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int[] v = new int[n+1];
int[] w = new int[n+1];
for(int i = 1; i <= n ; ++i) {
v[i] = scanner.nextInt();
w[i] = scanner.nextInt();
}
int[] f = new int[m+1];
for(int i = 1; i <= n ;++i ) {
for(int j = m ; j >= v[i] ; --j) {
f[j] = Math.max(f[j], f[j-v[i]]+w[i]);
}
}
System.out.println(f[m]);
}
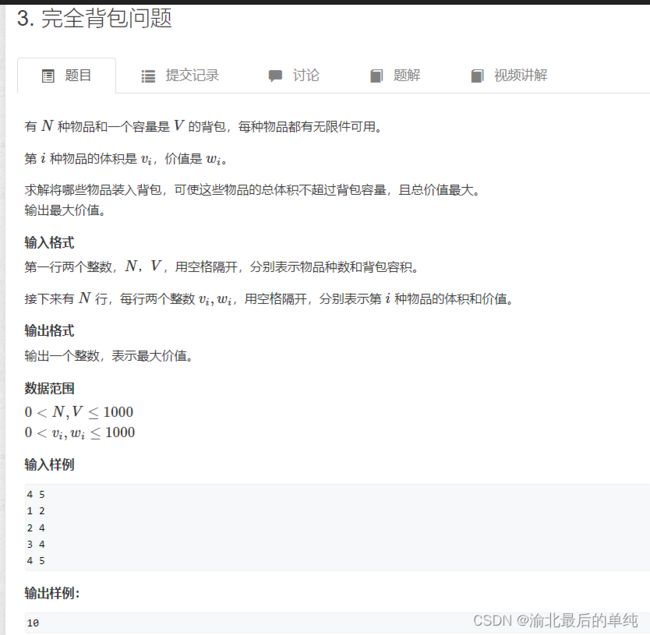
//完全背包
public static void packageFull() {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int f[] = new int[m+1];
for(int i = 1; i <= n ; ++i) {
int v = scanner.nextInt();
int w = scanner.nextInt();
for(int j = v ; j <= m ; ++j) {
f[j] = Math.max(f[j],f[j-v]+w);
}
}
System.out.println(f[m]);
}
class S{
int i;
int v , w;
public S(int s , int v , int w) {
this.i = s;
this.v = v*s;
this.w = w*s;
}
}
// 多重背包 有限物品 : 二进制算法改进 : eg: 9 可以有 1 2 4 1 任意三个数组成
public static void multiplePackage() {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
S[] pac = new S[1010];
int[] f = new int[m+1];
for(int h=1;h<=n;++h) {
int v = scanner.nextInt();
int w = scanner.nextInt();
int s = scanner.nextInt();
int cnt = 1;
for(int i = 1;s>= i; i*=2 ) {
s -= i;
pac[cnt++] = new S(i,v,w);
}
if(s>=0) {
pac[cnt] = new S(s,v,w);
}
for(int i = 1;i <= cnt ; i++) {
for(int j = m ; j >= pac[i].v;j--) {
f[j] = Math.max(f[j], f[j-pac[i].v]+pac[i].w);
}
}
}
System.out.println(f[m]);
}
class S{
int i;
int v , w;
public S(int s , int v , int w) {
this.i = s;
this.v = v*s;
this.w = w*s;
}
}
// 多重背包解法 只需要将 01背包 + 完全背包 + 多重背包(有限背包 进行2进制) 相叠加 进行动态规划
public static void complexPackage() {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
List<S> pac = new ArrayList<S>();
int[] f = new int[m + 1];
for (int h = 1; h <= n; ++h) {
int v = scanner.nextInt();
int w = scanner.nextInt();
int s = scanner.nextInt();
int x = s;
if (s > 0) {
for (int i = 1; s >= i; i *= 2) {
s -= i;
pac.add(new S(i, v, w));
}
if (s >= 0) {
pac.add(new S(s, v, w));
s= x;
}
} else if (s < 0) {
pac.add(new S(1, v, w));
} else {
pac.add(new S(1, v, w));
}
for (S ps : pac) {
if (s > 0 || s < 0) {
for (int j = m; j >= ps.v; j--) {
f[j] = Math.max(f[j], f[j - ps.v] + ps.w);
}
}else {
for(int j = ps.v ; j <= m ; j++) {
f[j] = Math.max(f[j], f[j-ps.v]+ps.w);
}
}
}
pac.clear();
}
System.out.println(f[m]);
}
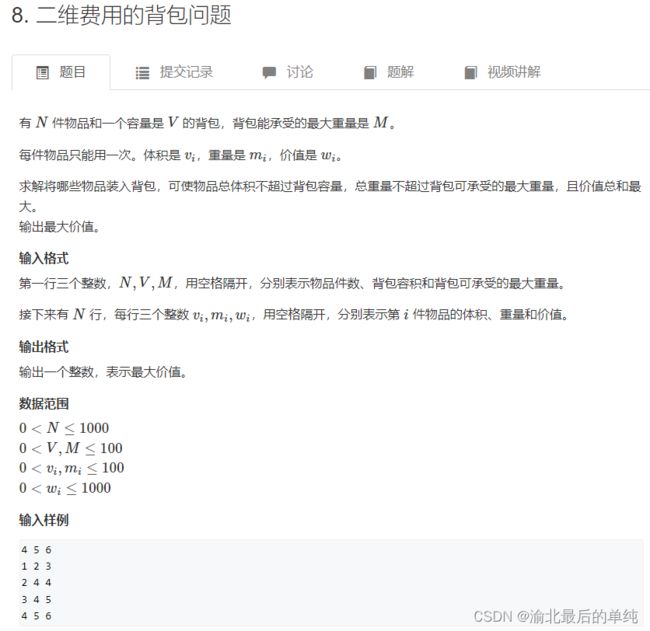
//二维背包解法
public static void doublePackage() {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt(); // N
int m = scanner.nextInt(); // max V
int l = scanner.nextInt(); // max weight;
int[] v = new int[n+1];
int[] w = new int[n+1];
int[] s = new int[n+1];
for(int i = 1; i <= n ; ++i) {
v[i] = scanner.nextInt(); // record V
s[i] = scanner.nextInt(); // record weight
w[i] = scanner.nextInt(); // record value
}
int[][] f = new int[m+1][l+1];
for(int i = 1; i <= n ;++i ) {
for(int j = m ; j >= v[i] ; --j) {
for(int k = l ; k>=s[i];--k) {
f[j][k] = Math.max(f[j][k], f[j-v[i]][k-s[i]]+w[i]);
}
}
}
System.out.println(f[m][l]);
}
public static void groupedPackage() {
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int m = scanner.nextInt();
int f[] = new int[m + 1];
int[] v = new int[105];
int[] w = new int[105];
for (int i = 1; i <= n; i++) {
int s = scanner.nextInt();
int cnt = 1;
for(int h = 1 ; h <= s ; h++) {
v[h] = scanner.nextInt();
w[h] = scanner.nextInt();
}
for (int j = m; j >= 1 ; j--,cnt++) {
for (int k = 1; k <= s; k++) {
if(j>=v[k]) f[j] = Math.max(f[j],f[j-v[k]]+w[k]); // 每次从 第i组中选择最适合的物品
}
}
}
System.out.println(f[m]);
}
单调栈类型
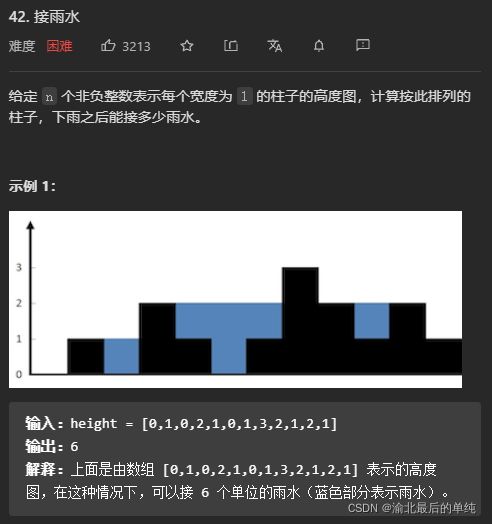
接雨水
1.单调栈
leetcode题解连接
https://assets.leetcode-cn.com/solution-static/42/f7.png
2.dp
public int trap(int[] height) {
int n = height.length;
int[] leftMax = new int[n+2];
int[] rightMax = new int[n+2];
for(int i = 1 ; i <= n ; ++i){
leftMax[i] = Math.max(height[i-1],leftMax[i-1]);
}
for(int i = n ; i >=1 ; --i){
rightMax[i] = Math.max(height[i-1],rightMax[i+1]);
}
int ans = 0;
for(int i = 1 ; i<= n ; ++i){
ans += Math.min(rightMax[i],leftMax[i])-height[i-1];
}
return ans;
最长上升子序列
通过栈的
import java.util.Scanner;
import java.util.Deque;
import java.util.LinkedList;
import java.util.ListIterator;
import java.util.*;
public class Main{
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
int [] arr = new int[n+1];
for(int i = 1 ; i<= n; ++i){
arr[i] = scanner.nextInt();
}
LinkedList<Integer> stack = new LinkedList<Integer>();
stack.push(arr[1]);
int cnt = 1 ;
int ans = 0;
for(int i = 2 ; i <= n ; ++i){
if(stack.peekLast() < arr[i]){
stack.add(arr[i]);
cnt++;
}else{
ListIterator<Integer> iterator = stack.listIterator();
while(iterator.hasNext()){
if(iterator.next() >= arr[i]){
iterator.set(new Integer(arr[i]));
break;
}
}
}
// for(Integer x : stack){
// System.out.print("stack:"+x);
// }
// System.out.println();
ans = Math.max(ans,cnt);
}
System.out.println(ans);
}
}
状态压缩
状态转移方程:
f [ i ] [ j ] = m i n ( f [ i ] [ j ] , f [ i − ( 1 < < j ) ] [ k ] + w [ k ] [ j ] ) f[i][j]=min(f[i][j],f[i-(1<
状态压缩DP分析:
1.本题思路
假设:一共有七个点,用0,1,2,3,4,5,6来表示,那么先假设终点就是5,在这里我们再假设还没有走到5这个点,且走到的终点是4,那么有以下六种情况:
first: 0–>1–>2–>3–>4 距离:21
second: 0–>1–>3–>2–>4 距离:23
third: 0–>2–>1–>3–>4 距离:17
fourth: 0–>2–>3–>1–>4 距离:20
fifth: 0–>3–>1–>2–>4 距离:15
sixth: 0–>3–>2–>1–>4 距离:18
如果此时你是一个商人你会走怎样的路径?显而易见,会走第五种情况对吧?因为每段路程的终点都是4,且每种方案的可供选择的点是04,而商人寻求的是走到5这个点的最短距离,而4到5的走法只有一种,所以我们选择第五种方案,可寻找到走到5这个点儿之前,且终点是4的方案的最短距离,此时05的最短距离为(15+4走到5的距离).(假设4–>5=8)
同理:假设还没有走到5这个点儿,且走到的终点是3,那么有一下六种情况:
first: 0–>1–>2–>4–>3 距离:27
second: 0–>1–>4–>2–>3 距离:22
third: 0–>2–>1–>4–>3 距离:19
fourth: 0–>2–>4–>1–>3 距离:24
fifth: 0–>4–>1–>2–>3 距离:26
sixth: 0–>4–>2–>1–>3 距离:17
此时我们可以果断的做出决定:走第六种方案!!!,而此时0~5的最短距离为(17+3走到5的距离)(假设3–>5=5)
在以上两大类情况之后我们可以得出当走到5时:
1.以4为终点的情况的最短距离是:15+8=23;
2.以3为终点的情况的最短距离是:17+5=22;
经过深思熟虑之后,商人决定走以3为终点的最短距离,此时更新最短距离为:22。
当然以此类推还会有以1为终点和以2为终点的情况,此时我们可以进行以上操作不断更新到5这个点的最短距离,最终可以得到走到5这个点儿的最短距离,然后再返回最初的假设,再依次假设1,2,3,4是终点,最后再不断更新,最终可以得出我们想要的答案
2.DP分析:
用二进制来表示要走的所以情况的路径,这里用i来代替
例如走0,1,2,4这三个点,则表示为:10111;
走0,2,3这三个点:1101;
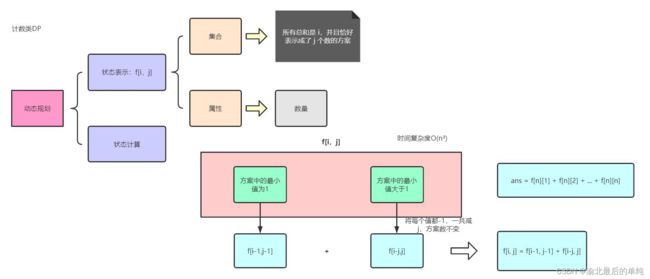
状态表示:f[i][j];
集合:所有从0走到j,走过的所有点的情况是i的所有路径
属性:MIN
状态计算:如1中分析一致,0–>·····–>k–>j中k的所有情况
#include
#include
#include
using namespace std;
const int N=20,M=1<>n;
for(int i=0;i>w[i][j];
memset(f,0x3f,sizeof(f));//因为要求最小值,所以初始化为无穷大
f[1][0]=0;//因为零是起点,所以f[1][0]=0;
for(int i=0;i<1<>j&1)
for(int k=0;k>k&1)
f[i][j]=min(f[i][j],f[i-(1< 最短编辑距离
状态表示:f[i] [j] 表示 从字符串a 的第i 个位置到 字符串b的 第j 个位置匹配
状态转移:
f[i-1] [j] + 1: 删除第i个位置的值
f[i] [j-1] +1 :插入第i个位置 与 j-1匹配
f[i-1] [j-1] + 1 : 替换第i个位置
f [ i ] [ j ] = m i n ( f [ i − 1 ] [ j ] , f [ i − 1 ] [ j − 1 ] , f [ i ] [ j − 1 ] ) + 1 f[i][j] = min(f[i-1][j],f[i-1][j-1],f[i][j-1])+1 f[i][j]=min(f[i−1][j],f[i−1][j−1],f[i][j−1])+1
当 a[i] == b[j] 时:
f [ i ] [ j ] = f [ i − 1 ] [ j − 1 ] f[i][j] = f[i-1][j-1] f[i][j]=f[i−1][j−1]
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner scanner = new Scanner(System.in);
int n = scanner.nextInt();
String a = scanner.next();
int m = scanner.nextInt();
String b = scanner.next();
int[][] f = new int[n+1][m+1];
for(int i = 0 ; i <= n ; ++i){
f[i][0] = i;
}
for(int i = 0 ; i <= m ; ++i){
f[0][i] = i;
}
for(int i = 1 ; i <= n ; ++i){
for(int j = 1 ; j <= m ; ++j){
f[i][j] = a.charAt(i-1) == b.charAt(j-1) ? f[i-1][j-1]:Math.min(f[i-1][j],Math.min(f[i-1][j-1],f[i][j-1]))+1;
}
}
System.out.println(f[n][m]);
}
}
记忆化搜索
import java.io.BufferedInputStream;
import java.util.*;
public class Main {
static int[][]arr = new int[301][301];
static int directX[] = new int[]{1,0,0,-1};
static int directY[] = new int[]{0,1,-1,0};
static int[][] f = new int[301][301];
static int r , c ;
public static void main(String args[]) {
Scanner sc = new Scanner(new BufferedInputStream(System.in));
r = sc.nextInt();
c = sc.nextInt();
// 初始化数组
for(int i = 1 ; i <= r ; ++i){
for(int j = 1 ; j <= c ; ++j){
arr[i][j] = sc.nextInt();
}
}
int maxLen = 0 ;
for(int i = 1 ; i <= r ; ++i){
for(int j = 1 ; j <= c ; ++j){
maxLen = Math.max(maxLen,dfs(i,j));
}
}
System.out.print(maxLen);
}
public static int dfs(int x, int y ){
if(f[x][y] != 0 ){
return f[x][y]; // 重点, 保证不会重复搜索, 记忆化搜索的特征
}
f[x][y] = 1;
for(int i = 0; i < 4 ; i++){
int newX = x + directX[i];
int newY = y + directY[i];
if(newX >= 1 && newX <= r && newY >= 1 && newY <= c && arr[newX][newY]< arr[x][y]){
f[x][y] = Math.max(f[x][y],dfs(newX,newY)+1);
}
}
return f[x][y];
}
}
树形DP (过两天更新)
数位DP
计数问题
思路:
注意: 核心 分情况分数位
1).当x = 0 的情况 , abc 应该为001~abc-1 即 为 abc-1
其他情况则为 000~abc-1 共 abc 种
2)当进行计算abc得情况时 : 右侧应当判断(dj > 0 && (i!= 0 || l != 0))
import java.util.Scanner;
public class Main{
public static void main(String[] args){
Scanner sc = new Scanner(System.in);
int a , b;
while(true) {
a = sc.nextInt();
b = sc.nextInt();
if(a==0||b==0) {
break;
}
for (int i = 0; i <= 9; ++i) {
if(a>b) {
int temp = a;
a = b;
b = temp;
}
System.out.print(cnt(b, i)-cnt(a - 1, i)+" ");
}
System.out.println();
}
}
public static int cnt(int x ,int i) {
int ans = 0;
int n = dgt(x); // 获取位数
for(int j = 1 ; j <= n ; ++j) {
// eg: 10j01
int mid = (int)Math.pow(10, j-1); // 第j位 10j01 => 10^2
int l = x / mid/10; // 左端的数位 10j01 => 10
int r = x%mid; // 右边数字的最大值 => 01
int dj = x/mid%10; // 得到第j位
if(i != 0 ) ans+=l*mid;
if(i == 0 && l != 0) ans+=(l-1)*mid;
if(dj > i && (i!=0 || l != 0)) ans+= mid;
//Q:值得注意的是,我这里删掉了 (i || l) ,why ? A : 1.如果 i==0 ,l!=0 ,是ok的 ,如上例 2. i!=0 , l == 0 ,也有意义 ,eg n==2210 ,算 千位上 2出现的次数 ,满足 dj == i == 2 != 0 , l == 0 。那么显然有210个 , 也就是 res+=r+1,这里r=210,所谓+1是考虑了2000这个数 3. 全是零的话 ,这个if是进不来的。因为 l==0 ,说明我们要考察最高位 ,暗示dj !=0 ,要是最高位dj == 0 数据就非法了;另外 i == 0 。怎么可能满足 dj == i 的条件.
if(dj == i &&(i!=0 || l != 0)) ans+= r+1;//同理
}
return ans;
}
public static int dgt(int x) {
int n = 0;
while(x>0) {
x /= 10;
n++;
}
return n;
}
}