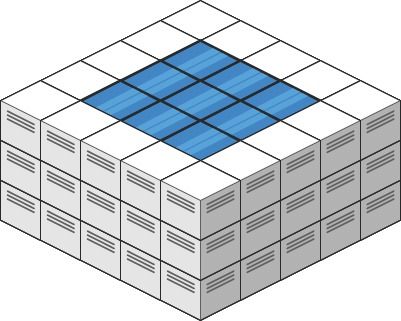
2021-11-03 LeetCode每日一题 407. 接雨水 II
问题描述:
给你一个 m x n 的矩阵,其中的值均为非负整数,代表二维高度图每个单元的高度,请计算图中形状最多能接多少体积的雨水。
示例 1:
输入: heightMap = [[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]]
输出: 4
解释: 下雨后,雨水将会被上图蓝色的方块中。总的接雨水量为1+2+1=4。示例 2:
输入: heightMap = [[3,3,3,3,3],[3,2,2,2,3],[3,2,1,2,3],[3,2,2,2,3],[3,3,3,3,3]]
输出: 10提示:
m == heightMap.length
n == heightMap[i].length
1 <= m, n <= 200
0 <= heightMap[i][j] <= 2 * 104解决方案:
class Solution:
def trapRainWater(self, heightMap: List[List[int]]) -> int:
if not heightMap or not heightMap[0]:
return 0
import heapq
m, n = len(heightMap), len(heightMap[0])
heap = []
visited = [[0]*n for _ in range(m)]
# Push all the block on the border into heap
for i in range(m):
for j in range(n):
if i == 0 or j == 0 or i == m-1 or j == n-1:
heapq.heappush(heap, (heightMap[i][j], i, j))
visited[i][j] = 1
result = 0
while heap:
height, i, j = heapq.heappop(heap)
for x, y in ((i+1, j), (i-1, j), (i, j+1), (i, j-1)):
if 0 <= x < m and 0 <= y < n and not visited[x][y]:
result += max(0, height-heightMap[x][y])
heapq.heappush(heap, (max(heightMap[x][y], height), x, y))
visited[x][y] = 1
return result