【torch高级】一种新型的概率学语言pyro(02/2)
前文链接:【torch高级】一种新型的概率学语言pyro(01/2)
七、Pyro 中的推理
7.1 背景:变分推理
引言中的每项计算(后验分布、边际似然和后验预测分布)都需要执行积分,而这通常是不可能的或计算上难以处理的。
虽然 Pyro 支持许多不同的精确和近似推理算法,但支持最好的是变分推理,它提供了一个统一的方案来查找![]() 并计算一个易于处理的近似值
并计算一个易于处理的近似值![]() 到真实的、未知的后验
到真实的、未知的后验![]() 通过将棘手的积分转换为函数的优化p和q。下图从概念上描述了这个过程,而SVI 教程中提供了更全面的数学介绍。
通过将棘手的积分转换为函数的优化p和q。下图从概念上描述了这个过程,而SVI 教程中提供了更全面的数学介绍。
大多数概率分布(下图中的浅色椭圆),尤其是那些对应于贝叶斯后验分布的概率分布,都太复杂而无法直接表示,因此我们必须定义一个更小的子空间,由实值参数索引![]() ,分布的
,分布的![]() , 通过构造保证可以轻松从中采样(下图中的黑圈),但可能不包括真实的后验分布
, 通过构造保证可以轻松从中采样(下图中的黑圈),但可能不包括真实的后验分布![]() (下图中的红星)。
(下图中的红星)。
变分推理通过搜索变分分布的空间来近似真实后验,根据某种距离或散度的度量(下图中的黑色箭头)找到与真实后验最相似的一个(下图中的黄色星星) 。
然而,有许多不同的方法来测量概率分布之间的距离或散度。我们应该选择哪一个呢?如图所示,理论上有吸引力的选择是 Kullback-Leibler 散度![]() ,但是直接计算它需要提前知道真实的后验,这会达不到目的。
,但是直接计算它需要提前知道真实的后验,这会达不到目的。
更重要的是,我们有兴趣优化这种散度,这可能听起来更难,但实际上可以使用贝叶斯定理重写定义![]() 作为一个不依赖于的棘手常数之间的差异
作为一个不依赖于的棘手常数之间的差异![]() 以及一个易于处理的术语,称为证据下界 (ELBO),定义如下。因此,最大化这个易于处理的项将产生与最小化原始 KL 散度相同的解决方案。
以及一个易于处理的术语,称为证据下界 (ELBO),定义如下。因此,最大化这个易于处理的项将产生与最小化原始 KL 散度相同的解决方案。
7.2 背景:“引导”程序作为灵活的近似后验
在变分推理中,我们引入参数化分布![]() 近似真实后验,其中
近似真实后验,其中![]() 称为变分参数。在许多文献中,这种分布被称为变分分布,在 Pyro 的上下文中,它被称为指南(一个音节而不是九个音节!)。
称为变分参数。在许多文献中,这种分布被称为变分分布,在 Pyro 的上下文中,它被称为指南(一个音节而不是九个音节!)。
就像模型一样,该指南被编码为guide()包含pyro.sample和pyro.param语句的 Python 程序。它不包含观察到的数据,因为指南需要是适当的标准化分布,以便易于从中采样。请注意,Pyro 强制执行这一点model(),并且guide()应该采用相同的参数。允许指南是任意的 Pyro 程序开启了编写指南系列的可能性,这些指南系列捕获更多真实后验的特定问题结构,仅在有用的方向上扩展搜索空间,如下图所示。
变分推理的数学对指南施加了哪些限制?由于该指南是后验的近似![]() ,指南需要提供模型中所有潜在随机变量的有效联合概率密度。回想一下,当使用原始语句在 Pyro 中指定随机变量时,
,指南需要提供模型中所有潜在随机变量的有效联合概率密度。回想一下,当使用原始语句在 Pyro 中指定随机变量时,pyro.sample()第一个参数表示随机变量的名称。这些名称将用于对齐模型和指南中的随机变量。非常明确地说,如果模型包含随机变量z_1
def model():
pyro.sample("z_1", ...)
那么指南需要有一个匹配的sample声明
def guide():
pyro.sample("z_1", ...)
两种情况中使用的分布可以不同,但名称必须一对一排列。
尽管它提供了灵活性,但手动编写指南可能会很困难且乏味,尤其是对于新用户而言。只要有可能,我们建议使用autoguides或配方,从pyro.infer.autoguide中随 Pyro 附带的模型自动生成通用指南系列。下一节将演示这两种方法。
7.3 示例:Pyro 中贝叶斯线性回归的平均场变分近似
对于贝叶斯线性回归的运行示例,我们将使用一个指南,将模型中未观察到的参数的分布建模为具有对角协方差的高斯分布,即假设潜在变量之间不存在相关性(这是一个很强的假设,因为我们应该看到)。这被称为平均场近似,这是一个借用自物理学的术语,这种近似最初是在物理学中发明的。
为了完整性,我们首先手工写出这种形式的引导程序。
[51]:
def custom_guide(is_cont_africa, ruggedness, log_gdp=None):
a_loc = pyro.param('a_loc', lambda: torch.tensor(0.))
a_scale = pyro.param('a_scale', lambda: torch.tensor(1.),
constraint=constraints.positive)
sigma_loc = pyro.param('sigma_loc', lambda: torch.tensor(1.),
constraint=constraints.positive)
weights_loc = pyro.param('weights_loc', lambda: torch.randn(3))
weights_scale = pyro.param('weights_scale', lambda: torch.ones(3),
constraint=constraints.positive)
a = pyro.sample("a", dist.Normal(a_loc, a_scale))
b_a = pyro.sample("bA", dist.Normal(weights_loc[0], weights_scale[0]))
b_r = pyro.sample("bR", dist.Normal(weights_loc[1], weights_scale[1]))
b_ar = pyro.sample("bAR", dist.Normal(weights_loc[2], weights_scale[2]))
sigma = pyro.sample("sigma", dist.Normal(sigma_loc, torch.tensor(0.05)))
return {"a": a, "b_a": b_a, "b_r": b_r, "b_ar": b_ar, "sigma": sigma}
我们可以使用pyro.render_model来可视化custom_guide,证明随机变量确实彼此独立,正如它们之间缺乏边缘所表明的那样。
[52]:
pyro.render_model(custom_guide, model_args=(is_cont_africa, ruggedness, log_gdp), render_params=True)
[52]:
Pyro 还包含大量“自动指南”,可根据给定模型自动生成指南程序。就像我们的手写指南一样,所有pyro.autoguide.AutoGuide实例(它们本身只是采用与模型相同的参数的函数)都返回它们包含的每个pyro.sample站点的值字典。
最简单的自动指南类是AutoNormal,它会在一行代码中自动生成一个指南,相当于我们上面手动编写的代码:
[53]:
auto_guide = pyro.infer.autoguide.AutoNormal(model)
然而,该指南本身并未完全指定推理算法:它仅描述了由参数(上图中的黑圈)索引的可能近似后验分布的搜索空间以及由初始参数值确定的该空间中的初始点。然后,我们必须通过解决参数的优化问题(上图中的黄色星星)来将该初始分布移向真实的后验分布(上图中的红色星星)。制定并解决这个优化问题是接下来两节的主题。
7.4 背景:估计和优化证据下限 (ELBO)
模型的功能![]() 并指导
并指导![]() 我们将优化的是 ELBO,定义为对指南中样本的期望:
我们将优化的是 ELBO,定义为对指南中样本的期望:
![]()
通过假设,我们可以计算期望内的所有概率,并且由于指南![]() 假设是我们可以从中采样的参数分布,我们可以计算该数量的蒙特卡罗估计以及模型和引导参数的梯度,
假设是我们可以从中采样的参数分布,我们可以计算该数量的蒙特卡罗估计以及模型和引导参数的梯度,![]() 。
。
通过模型和导向参数![]() 优化 ELBO , 通过使用这些梯度估计的随机梯度下降有时称为随机变分推理(SVI);有关 SVI 的详细介绍,请参阅SVI 第 I 部分。
优化 ELBO , 通过使用这些梯度估计的随机梯度下降有时称为随机变分推理(SVI);有关 SVI 的详细介绍,请参阅SVI 第 I 部分。
7.5 示例:通过随机变分推理 (SVI) 的贝叶斯回归
Pyro 包含ELBO 估计器的 许多不同实现(在上一节中以数学方式定义),每个估计器通过不同的权衡计算损失和梯度略有不同。 在本教程中,我们将仅使用pyro.infer.Trace_ELBO,这始终是正确且安全的;其他 ELBO 估计器可以为某些模型和指南提供计算或统计优势。
pyro.infer.Trace_ELBO我们将在示例模型中使用 SVI 进行推理,演示 Pyro 如何使用 PyTorch 的随机梯度下降实现来优化我们传递给pyro.infer.SVI的对象的输出,这是一个帮助器类,其step()方法负责计算损失和参数梯度并对参数应用更新和约束。
[54]:
adam = pyro.optim.Adam({"lr": 0.02})
elbo = pyro.infer.Trace_ELBO()
svi = pyro.infer.SVI(model, auto_guide, adam, elbo)
这里的pyro.optim.Adam是PyTorch优化器torch.optim.Adam的一个薄包装器(请参见此处的讨论)。中的优化器pyro.optim用于优化和更新 Pyro 参数存储中的参数值。特别是,您会注意到我们不需要将可学习的参数传递给优化器,因为这是由指导代码确定的,并且在类的幕后SVI自动发生。要采取 ELBO 梯度步骤,我们只需调用 SVI 的步骤方法。我们传递给的 data 参数SVI.step将同时传递给model()和guide()。完整的训练循环如下:
[55]:
%%time
pyro.clear_param_store()
# These should be reset each training loop.
auto_guide = pyro.infer.autoguide.AutoNormal(model)
adam = pyro.optim.Adam({"lr": 0.02}) # Consider decreasing learning rate.
elbo = pyro.infer.Trace_ELBO()
svi = pyro.infer.SVI(model, auto_guide, adam, elbo)
losses = []
for step in range(1000 if not smoke_test else 2): # Consider running for more steps.
loss = svi.step(is_cont_africa, ruggedness, log_gdp)
losses.append(loss)
if step % 100 == 0:
logging.info("Elbo loss: {}".format(loss))
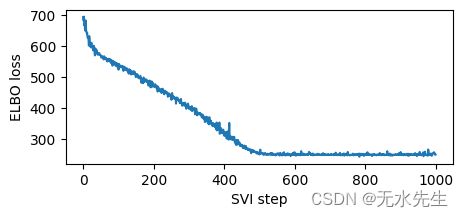
plt.figure(figsize=(5, 2))
plt.plot(losses)
plt.xlabel("SVI step")
plt.ylabel("ELBO loss");
埃尔博损失:694.9404826164246 埃尔博损失:524.3822101354599 埃尔博损失:475.66820669174194 埃尔博损失:399.99088364839554 埃尔博损失:315.23274326324463 埃尔博损失:254.76771265268326 埃尔博损失:248.237040579319 埃尔博损失:248.42670530080795 埃尔博损失:248.46450632810593 埃尔博损失:257.41463351249695
CPU时间:用户6.47秒,系统:241微秒,总计:6.47秒 挂壁时间:6.28 秒
[55]:
Text(0, 0.5, 'ELBO 损失')
请注意,由于我们使用了高学习率,因此训练速度很快。有时模型和指南对学习率很敏感,首先要尝试的是降低学习率并增加步数。这对于深度神经网络的模型和指南尤其重要。我们建议从较低的学习率开始,然后逐渐增加,避免学习率太快,否则推理可能会发散或导致 NAN。
训练完向导后,我们可以通过从 Pyro 的参数存储中获取优化的向导参数值来检查。下面打印的每个(loc,scale)对参数化指南中的单个pyro.distributions.Normal分布,对应于模型中不同的未观察到的pyro.sample语句,类似于我们之前手写的custom_guide。
[56]:
for name, value in pyro.get_param_store().items():
print(name, pyro.param(name).data.cpu().numpy())
自动法线.locs.a 9.173145 自动法线.scales.a 0.0703669 自动法线.locs.bA -1.8474661 自动正态.scales.bA 0.1407009 自动法线.locs.bR -0.19032118 自动法线.scales.bR 0.044044234 自动法线.locs.bAR 0.35599768 自动正态.scales.bAR 0.079374395 自动法线.locs.sigma -2.205863 自动正态.scales.sigma 0.060526706
最后,让我们重新审视之前的问题,即地形崎岖度与 GDP 之间的关系对于模型参数估计的任何不确定性有多稳健。为此,我们绘制了考虑到非洲境内和境外国家地形崎岖程度的 GDP 对数斜率分布。
我们用从我们训练有素的指南中抽取的样本来表示这两种分布。要并行绘制多个样本,我们可以在pyro.plate 语句中调用指南,该语句重复并向量化指南中每个pyro.sample 语句的采样操作,如介绍pyro.plate 原语部分中所述。
[57]:
with pyro.plate("samples", 800, dim=-1):
samples = auto_guide(is_cont_africa, ruggedness)
gamma_within_africa = samples["bR"] + samples["bAR"]
gamma_outside_africa = samples["bR"]
如下所示,非洲国家的概率质量主要集中在正区域,其他国家反之亦然,这进一步证实了最初的假设。然而,非非洲国家的后验不确定性(橙色直方图的宽度)似乎远低于非洲国家(蓝色直方图的宽度),考虑到原始数据中看似相似的分布,这是令人惊讶的。我们将在下一节中进一步研究这种差异。
[58]:
fig = plt.figure(figsize=(10, 6))
sns.histplot(gamma_within_africa.detach().cpu().numpy(), kde=True, stat="density", label="African nations")
sns.histplot(gamma_outside_africa.detach().cpu().numpy(), kde=True, stat="density", label="Non-African nations", color="orange")
fig.suptitle("Density of Slope : log(GDP) vs. Terrain Ruggedness");
plt.xlabel("Slope of regression line")
plt.legend()
plt.show()
八、Pyro 中的模型评估
8.1 背景:使用后验预测检查的贝叶斯模型评估
为了评估我们是否可以相信我们的推理结果,我们将比较我们的模型诱导的可能新数据的后验预测分布与现有的观察到的数据。一般来说,计算这个分布是很棘手的,因为它取决于知道真实的后验,但我们可以使用从变分推理获得的近似后验轻松地近似它:
具体来说,要从后验预测中抽取近似样本,我们只需抽取一个样本![]() 从近似后验,然后从给定样本的模型中观察到的变量的分布中进行采样
从近似后验,然后从给定样本的模型中观察到的变量的分布中进行采样![]() ,就好像我们用(近似的)后验替换了先验。
,就好像我们用(近似的)后验替换了先验。
8.2 示例:Pyro 中的后验预测不确定性
为了评估我们的示例线性回归模型,我们将使用Predictive实用程序类生成并可视化后验预测分布中的一些样本,该实用程序类实现了上面的方法,用于大约从![]() 。
。
我们从经过训练的模型中生成 800 个样本。在内部,这是通过首先从 中生成潜在变量的样本guide,然后向前运行模型,同时将未观察到的pyro.sample语句返回的值更改为从 中采样的相应值来完成的guide。
[59]:
predictive = pyro.infer.Predictive(model, guide=auto_guide, num_samples=800) svi_samples = predictive(is_cont_africa, ruggedness, log_gdp=None) svi_gdp = svi_samples["obs"]
下面的代码特定于此示例,仅用于绘制每个国家的后验预测分布的 90% 可信区间(包含 90% 的概率质量的区间)。
[60]:
predictions = pd.DataFrame({
"cont_africa": is_cont_africa,
"rugged": ruggedness,
"y_mean": svi_gdp.mean(0).detach().cpu().numpy(),
"y_perc_5": svi_gdp.kthvalue(int(len(svi_gdp) * 0.05), dim=0)[0].detach().cpu().numpy(),
"y_perc_95": svi_gdp.kthvalue(int(len(svi_gdp) * 0.95), dim=0)[0].detach().cpu().numpy(),
"true_gdp": log_gdp,
})
african_nations = predictions[predictions["cont_africa"] == 1].sort_values(by=["rugged"])
non_african_nations = predictions[predictions["cont_africa"] == 0].sort_values(by=["rugged"])
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
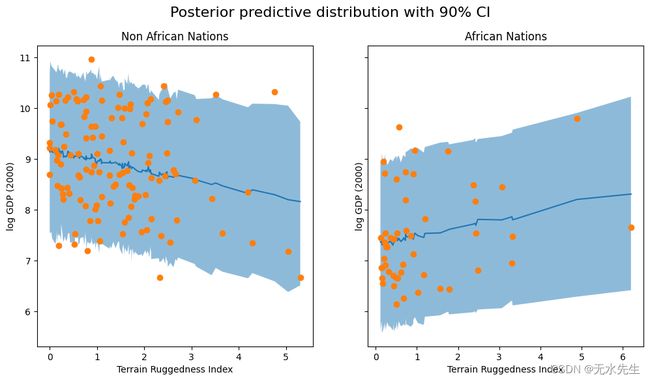
fig.suptitle("Posterior predictive distribution with 90% CI", fontsize=16)
ax[0].plot(non_african_nations["rugged"], non_african_nations["y_mean"])
ax[0].fill_between(non_african_nations["rugged"], non_african_nations["y_perc_5"], non_african_nations["y_perc_95"], alpha=0.5)
ax[0].plot(non_african_nations["rugged"], non_african_nations["true_gdp"], "o")
ax[0].set(xlabel="Terrain Ruggedness Index", ylabel="log GDP (2000)", title="Non African Nations")
ax[1].plot(african_nations["rugged"], african_nations["y_mean"])
ax[1].fill_between(african_nations["rugged"], african_nations["y_perc_5"], african_nations["y_perc_95"], alpha=0.5)
ax[1].plot(african_nations["rugged"], african_nations["true_gdp"], "o")
ax[1].set(xlabel="Terrain Ruggedness Index", ylabel="log GDP (2000)", title="African Nations");
我们观察到,我们的模型和 90% CI 的结果占了我们在实践中观察到的大部分数据点,但仍有相当多的非非洲国家被我们的近似后验认为是不可能的。
8.3 示例:使用满秩指南重新审视贝叶斯回归
为了改进我们的结果,我们将尝试使用从所有参数的多元正态分布生成样本的指南。这使我们能够通过满秩协方差矩阵捕获潜在变量之间的相关性![]() ; 我们之前的指南忽略了这些相关性。也就是说,我们有
; 我们之前的指南忽略了这些相关性。也就是说,我们有
![]()
要手动编写这种形式的指南,我们需要组合所有潜在变量,以便我们可以将pyro.sample它们从单个pyro.distributions.MultivariateNormal分布中组合在一起,选择一个实现constrain()来固定值![]() 为了积极,创建并初始化参数
为了积极,创建并初始化参数![]() 适当的形状,并约束变分参数Σ在整个优化过程中保持有效的协方差矩阵(即保持正定)。
适当的形状,并约束变分参数Σ在整个优化过程中保持有效的协方差矩阵(即保持正定)。
这将非常乏味,因此我们将使用另一个自动指南来为我们处理所有这些簿记工作,pyro.infer.autoguide.AutoMultivariateNormal:
[61]:
mvn_guide = pyro.infer.autoguide.AutoMultivariateNormal(model)
使用pyro.render_model表明,与我们的平均场AutoNormal指南不同,本指南明确捕获了模型中所有潜在变量之间的相关性。可视化图中的新_AutoMultivariateNormal_latent节点对应于上面的等式;与模型变量相对应的其他节点只是简单地索引到该张量值随机变量的各个元素。
[62]:
pyro.render_model(mvn_guide, model_args=(is_cont_africa, ruggedness, log_gdp), render_params=True)
[62]:
我们的模型以及其余的推理和评估代码与以前相比基本上没有变化:我们使用pyro.optim.Adam和pyro.infer.Trace_ELBO来拟合新指南的参数,然后从指南中采样并使用Predictive从后验预测分布中采样。
Predictive有一个值得注意的细微差别:我们通过关键字参数直接将指南样本传递给预测,posterior_samples而不是像上一节那样传递指南,从而重用指南样本进行预测。这避免了不必要的重复计算。
[63]:
%%time
pyro.clear_param_store()
mvn_guide = pyro.infer.autoguide.AutoMultivariateNormal(model)
svi = pyro.infer.SVI(model,
mvn_guide,
pyro.optim.Adam({"lr": 0.02}),
pyro.infer.Trace_ELBO())
losses = []
for step in range(1000 if not smoke_test else 2):
loss = svi.step(is_cont_africa, ruggedness, log_gdp)
losses.append(loss)
if step % 100 == 0:
logging.info("Elbo loss: {}".format(loss))
plt.figure(figsize=(5, 2))
plt.plot(losses)
plt.xlabel("SVI step")
plt.ylabel("ELBO loss")
with pyro.plate("samples", 800, dim=-1):
mvn_samples = mvn_guide(is_cont_africa, ruggedness)
mvn_gamma_within_africa = mvn_samples["bR"] + mvn_samples["bAR"]
mvn_gamma_outside_africa = mvn_samples["bR"]
# Interface note: reuse guide samples for prediction by passing them to Predictive
# via the posterior_samples keyword argument instead of passing the guide as above
assert "obs" not in mvn_samples
mvn_predictive = pyro.infer.Predictive(model, posterior_samples=mvn_samples)
mvn_predictive_samples = mvn_predictive(is_cont_africa, ruggedness, log_gdp=None)
mvn_gdp = mvn_predictive_samples["obs"]
埃尔博损失:702.4906432628632 埃尔博损失:548.7575962543488 埃尔博损失:490.9642730951309 埃尔博损失:401.81392109394073 埃尔博损失:333.7779414653778 埃尔博损失:247.01823914051056 埃尔博损失:248.3894298672676 埃尔博损失:247.3512134552002 埃尔博损失:248.2095948457718 埃尔博损失:247.21006780862808
CPU时间:用户1分钟45秒,系统:21.9毫秒,总计:1分钟45秒 挂壁时间:7.03 秒
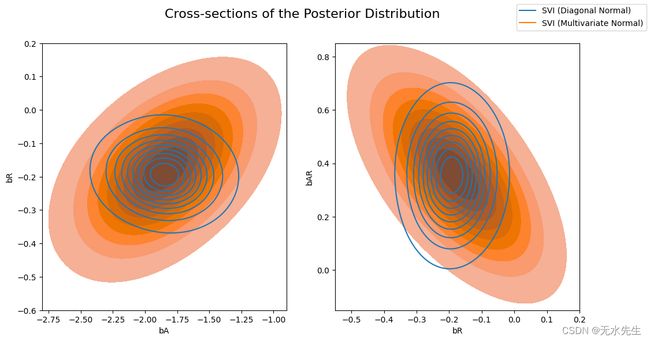
现在让我们比较一下前一个AutoDiagonalNormal指南与AutoMultivariateNormal指南计算的后验概率。我们将在视觉上叠加后验分布的横截面(回归系数对的联合分布)。
请注意,多元正态近似比平均场近似更加分散,并且能够对后验系数之间的相关性进行建模。
[64]:
svi_samples = {k: v.detach().cpu().numpy() for k, v in samples.items()}
svi_mvn_samples = {k: v.detach().cpu().numpy() for k, v in mvn_samples.items()}
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
fig.suptitle("Cross-sections of the Posterior Distribution", fontsize=16)
sns.kdeplot(x=svi_samples["bA"], y=svi_samples["bR"], ax=axs[0], bw_adjust=4 )
sns.kdeplot(x=svi_mvn_samples["bA"], y=svi_mvn_samples["bR"], ax=axs[0], shade=True, bw_adjust=4)
axs[0].set(xlabel="bA", ylabel="bR", xlim=(-2.8, -0.9), ylim=(-0.6, 0.2))
sns.kdeplot(x=svi_samples["bR"], y=svi_samples["bAR"], ax=axs[1],bw_adjust=4 )
sns.kdeplot(x=svi_mvn_samples["bR"], y=svi_mvn_samples["bAR"], ax=axs[1], shade=True, bw_adjust=4)
axs[1].set(xlabel="bR", ylabel="bAR", xlim=(-0.55, 0.2), ylim=(-0.15, 0.85))
for label, color in zip(["SVI (Diagonal Normal)", "SVI (Multivariate Normal)"], sns.color_palette()[:2]):
plt.plot([], [],
label=label, color=color)
fig.legend(loc='upper right')
[64]:
通过重复我们对非洲内外国家的坚固性-GDP 系数分布的可视化,我们可以看到这一点的含义。现在,两个系数中每个系数的后验不确定性大致相同,这与目测数据所表明的结果一致。
[65]:
fig, axs = plt.subplots(nrows=1, ncols=2, figsize=(12, 6))
fig.suptitle("Density of Slope : log(GDP) vs. Terrain Ruggedness");
sns.histplot(gamma_within_africa.detach().cpu().numpy(), ax=axs[0], kde=True, stat="density", label="African nations")
sns.histplot(gamma_outside_africa.detach().cpu().numpy(), ax=axs[0], kde=True, stat="density", color="orange", label="Non-African nations")
axs[0].set(title="Mean field", xlabel="Slope of regression line", xlim=(-0.6, 0.6), ylim=(0, 11))
sns.histplot(mvn_gamma_within_africa.detach().cpu().numpy(), ax=axs[1], kde=True, stat="density", label="African nations")
sns.histplot(mvn_gamma_outside_africa.detach().cpu().numpy(), ax=axs[1], kde=True, stat="density", color="orange", label="Non-African nations")
axs[1].set(title="Full rank", xlabel="Slope of regression line", xlim=(-0.6, 0.6), ylim=(0, 11))
handles, labels = axs[1].get_legend_handles_labels()
fig.legend(handles, labels, loc='upper right');
我们在两种近似下可视化非非洲国家后验预测分布的 90% 可信区间,验证我们对观测数据的覆盖范围有所改善:
[66]:
mvn_predictions = pd.DataFrame({
"cont_africa": is_cont_africa,
"rugged": ruggedness,
"y_mean": mvn_gdp.mean(dim=0).detach().cpu().numpy(),
"y_perc_5": mvn_gdp.kthvalue(int(len(mvn_gdp) * 0.05), dim=0)[0].detach().cpu().numpy(),
"y_perc_95": mvn_gdp.kthvalue(int(len(mvn_gdp) * 0.95), dim=0)[0].detach().cpu().numpy(),
"true_gdp": log_gdp,
})
mvn_non_african_nations = mvn_predictions[mvn_predictions["cont_africa"] == 0].sort_values(by=["rugged"])
fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(12, 6), sharey=True)
fig.suptitle("Posterior predictive distribution with 90% CI", fontsize=16)
ax[0].plot(non_african_nations["rugged"], non_african_nations["y_mean"])
ax[0].fill_between(non_african_nations["rugged"], non_african_nations["y_perc_5"], non_african_nations["y_perc_95"], alpha=0.5)
ax[0].plot(non_african_nations["rugged"], non_african_nations["true_gdp"], "o")
ax[0].set(xlabel="Terrain Ruggedness Index", ylabel="log GDP (2000)", title="Non African Nations: Mean-field")
ax[1].plot(mvn_non_african_nations["rugged"], mvn_non_african_nations["y_mean"])
ax[1].fill_between(mvn_non_african_nations["rugged"], mvn_non_african_nations["y_perc_5"], mvn_non_african_nations["y_perc_95"], alpha=0.5)
ax[1].plot(mvn_non_african_nations["rugged"], mvn_non_african_nations["true_gdp"], "o")
ax[1].set(xlabel="Terrain Ruggedness Index", ylabel="log GDP (2000)", title="Non-African Nations: Full rank");
8.4 下一步
如果您已经完成了这一步,那么您就可以开始使用 Pyro 了!按照首页上的说明安装 Pyro并查看我们其余的示例和教程,特别是实用 Pyro 和 PyTorch教程系列,其中包括本教程中使用更原生 PyTorch编写的相同贝叶斯回归分析的版本建模API。
有关 Pyro 中变分推理数学的更多背景信息,请查看我们的 SVI 教程系列,从第 1 部分开始。如果您是 PyTorch 或深度学习的新手,您也可能会从阅读官方介绍“使用 PyTorch 进行深度学习”中受益。
大多数达到这一点的用户还会在 Pyro 基本读物中找到我们的张量形状指南。Pyro 广泛使用PyTorch 和其他数组库中的“数组广播”行为来并行化模型和推理算法,虽然最初可能很难理解这种行为,但应用直觉和经验法则将会有很长的路要走。使您的体验顺畅并避免令人讨厌的形状错误的方法。