毕业设计（四）-- 指针式仪表读数

1  图像预处理

    1.1  中值滤波

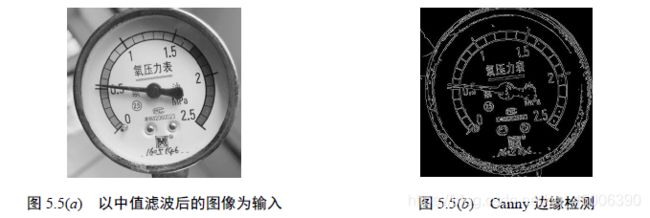
    为了使输入图像更加清晰，需要对其进行去噪。在常用的去噪算法中，中值滤波可以很好的保留边缘信息同时去除噪点，中值滤波的原理是对矩阵中的像素值进行排序，并用序列中值替换该矩阵中心的数据。

    中心点像素为0 处在图像上表现为一个噪点，经过中值滤波处理后，像素0 被替换为像素6。从数值变化的角度上，中值滤波是一种非线性变换，它只对矩阵中心点的像素进行了改变，对矩阵外围的像素数值没有进行改变；从图像的角度上，中值滤波可以对图像进行去噪，同时保留了更多的边缘信息。

   1.2  边缘检测

    通过Canny 边缘检测，可以对去噪后的图像进一步处理，提取出图像中指针与刻度的边缘信息。Canny 边缘检测主要包括以下几个步骤：

    1）Sobel 算子计算像素梯度：

    图像中的边缘是灰度变化最明显的地方，利用Sobel 算子来提取图像中每个像素的梯度，灰度变化越大梯度也就越大，通过对像素梯度的提取也就相当于提取了所有可能存在的边缘。下面利用一个3*3 大小的Sobel 算子模板A，对输入图像可以进行x 轴与y 轴两个方向上的梯度计算。

    Sobel 算子引入中心系数2，模板A 在x 轴与y 轴方向上的梯度Gx 与Gy 计算公式如下：

    因此x 轴与y 轴方向上的Sobel 算子也表现为以下两种形式：

    Sobel 算子在x 轴与y 轴方向上采用一阶导数的方式进行梯度的计算，对于直线及边缘都具有很好的检测能力。

    2）梯度方向非极大值抑制：

    对于图像中的灰度变化明显的区域，Sobel 算子提取了许多相近的梯度，为了能使提取出的边缘能够清晰，需要通过非极大值抑制来对梯度进行筛选。

    根据大小为3*3 的Sobel 算子模板A 的x 轴与y 轴方向上的梯度Gx 与Gy，可以计算出梯度大小G 与梯度方向：

    在局部的范围内，对于梯度方向相同的像素点进行梯度大小G 之间的比较，只保留梯度最大的像素点，减少了相近的梯度数量。

    3）双阈值检测边缘：

    Canny 边缘检测采用双阈值来进行梯度筛选，其原因在于单阈值筛选只保留大于最高阈值的边缘，那么边缘可能出现无法闭合的问题。而双阈值通过设置一个最小阈值，将最小阈值以下的梯度删去，保留最小阈值与最大阈值之间的梯度作为待定边缘。如果高于最大阈值的梯度所构成的边缘无法闭合，则从待定边缘中选取相应区域的梯度作为补充，使得提取出的边缘都能尽可能闭合。

    Canny 边缘检测的最大优点也体现在可以通过对双阈值的调节，来保留下所需要的信息，去掉不需要的噪声。对于指针式仪表而言，要尽可能保留下指针与刻度部分的信息，其他如仪表外壳或者无关的表示则无需保留。

    当上下阈值差值固定为100 时，随着阈值的提升，越来越多无关的信息在边缘检测中被删去，所需要的指针位置以及量程刻度信息被保留下来。但是，当阈值过大时如图5.6(f)所示，也会导致一些重要信息被误删，因此在实际应用中需要根据实际情况对上下阈值进行调整。

1.2  霍夫变换检测指针

    图像空间中的线与参数空间中的点具有对应关系，霍夫变换(Hough Transform)的核心思想是将输入的图像映射到参数空间中，通过投票算法来计算出现次数最多的参数值，并将参数值代入相应的特征方程就可以得出需要检测的图形。

    假设在图像空间中存在一点A(x0, y0)，经过点A 的直线m 为其斜率，c 是其截距，则该直线的特征方程在直角坐标系中可表示为：

    当m 趋于无穷大，直角坐标系无法表示垂直于x 轴时的直线特征方程，需要将直角坐标系方程转化为极坐标系方程：

    将图像空间中的一条直线映射至参数空间，将数据统计于下表：

    通过出现次数的统计，可以给出相应的直线方程为：

    为了能够对输入的指针式仪表图像进行读数，就需要从图像中提取出指针以及量程刻度等有效信息，对于圆形与矩形的指针式仪表，均可以采用霍夫变换在表盘中检测出指针以及量程刻度。

    对于圆形指针式仪表，需要检测出其指针、开始刻度以及结束刻度所在的直线，并返回相应的角度；而对于矩形指针式仪表，由于其开始刻度与上下边框平行，结束刻度与左右刻度平行，所以只需要检测出指针、下边框以及右侧边框所在直线并返回角度即可。

1.3  指针式仪表读数

    在霍夫直线检测中，每条被检测出的直线都采用极坐标系方程的形式来表示，因此每条直线都会返回两个特征值，分别为极坐标系原点到这条直线的距离(rho)和这条直线与极坐标系横轴所成角的角度(theta)。由于指针式仪表的刻度分布均匀，因此可以根据仪表量程刻度的开始角度与结束角度，配合指针所在直线返回的角度进行读数。

    1.3.1  圆形指针式仪表读数计算

    对于圆形指针式仪表一共检测了三条直线：指针所在直线z、开始刻度所在直线k 和结束刻度所在直线j，分别记录其角度。

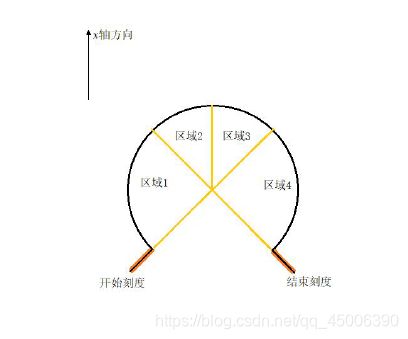
    霍夫变换所确定的极坐标系中，其x 轴方向如下图所示。如果直线落在x 轴的右半平面，那么霍夫变换所返回的角度就等于该直线的真实角度；如果直线落在x 轴的右平面，那么霍夫变换的所返回的角度等于该直线反向延长线在左平面与x 轴构成的角度。

    作开始刻度与结束刻度的延长线相交于一点，由该点做x 轴的平行线，可将仪表盘的量
程划分为四个区域：

    区域3 对应着返回的角度k，区域3 和区域4 对应着返回角度j，整体的量程刻度对应着区域1、区域2、区域3 以及区域4 之和，用表达式可表述为：

    1）若指针落在区域1：此时指针的反向延长线落在区域4，指针与开始刻度所成角度就等于二者反向延长线所成角度：

    2）若指针落在区域1：此时指针的反向延长线落在区域4 的右侧，指针与开始刻度所成角度就等于二者反向延长线所成角度：

    3）若指针落在区域3：此时无需对指针进行反向延长，指针与开始刻度所成角度等于减去开始刻度反向延长线与指针所成角度：

    4）若指针落在区域4：此时无需对指针进行反向延长，指针与开始刻度所成角度等于加上指针与开始刻度反向延长线所成角度：

    根据指针落在的区域选择合适的，带入表达式(5-8)便可完成对矩形仪表的读数：

 

    对以上选取出的指针式仪表进行读数，并统计其相对误差和引用误差如下表：

    通过误差分析可以发现，利用OpenCV 对仪表进行读数效果理想，其中圆形指针式仪表相对误差之所以较高，主要是因为利用角度法进行读数受仪表刻度划分影响较大，如果量程刻度分布不够密集，那么角度上的细微偏差就会体现为数值上的较大偏差。对于圆形指针式仪表而言，如果其量程较小，那么其划分的刻度就会比较稀疏，这也使得其相对误差较大。从算法读数的整体效果而言，其相对误差均值和引用误差均值符合生产生活的日常需求。