07-链表(下):如何轻松写出正确的链表代码
上一节讲了链表相关的基础知识。学完之后,我看到有人留言说,基础知识我都掌握了,但是写链表代码还是很费劲。哈哈,的确是这样的!
想要写好链表代码并不是容易的事儿,尤其是那些复杂的链表操作,比如链表反转、有序链表合并等,写的时候非常容易出错。从我上百场面试的经验来看,能把“链表反转”这几行代码写对的人不足 10%。
为什么链表代码这么难写?究竟怎样才能比较轻松地写出正确的链表代码呢?
只要愿意投入时间,我觉得大多数人都是可以学会的。比如说,如果你真的能花上一个周末或者一整天的时间,就去写链表反转这一个代码,多写几遍,一直练到能毫不费力地写出 Bug free 的代码。这个坎还会很难跨吗?
当然,自己有决心并且付出精力是成功的先决条件,除此之外,我们还需要一些方法和技巧。我根据自己的学习经历和工作经验,总结了几个写链表代码技巧。如果你能熟练掌握这几个技巧,加上你的主动和坚持,轻松拿下链表代码完全没有问题。
技巧一:理解指针或引用的含义
事实上,看懂链表的结构并不是很难,但是一旦把它和指针混在一起,就很容易让人摸不着头脑。所以,要想写对链表代码,首先就要理解好指针。
我们知道,有些语言有“指针”的概念,比如 C 语言;有些语言没有指针,取而代之的是“引用”,比如 Java、Python。不管是“指针”还是“引用”,实际上,它们的意思都是一样的,都是存储所指对象的内存地址。
接下来,我会拿 C 语言中的“指针”来讲解,如果你用的是 Java 或者其他没有指针的语言也没关系,你把它理解成“引用”就可以了。
实际上,对于指针的理解,你只需要记住下面这句话就可以了:
将某个变量赋值给指针,实际上就是将这个变量的地址赋值给指针,或者反过来说,指针中存储了这个变量的内存地址,指向了这个变量,通过指针就能找到这个变量。
这句话听起来还挺拗口的,你可以先记住。我们回到链表代码的编写过程中,我来慢慢给你解释。
在编写链表代码的时候,我们经常会有这样的代码:p->next=q。这行代码是说,p 结点中的 next 指针存储了 q 结点的内存地址。
还有一个更复杂的,也是我们写链表代码经常会用到的:p->next=p->next->next。这行代码表示,p 结点的 next 指针存储了 p 结点的下下一个结点的内存地址。
掌握了指针或引用的概念,你应该可以很轻松地看懂链表代码。恭喜你,已经离写出链表代码近了一步!
技巧二:警惕指针丢失和内存泄漏
不知道你有没有这样的感觉,写链表代码的时候,指针指来指去,一会儿就不知道指到哪里了。所以,我们在写的时候,一定注意不要弄丢了指针。
指针往往都是怎么弄丢的呢?我拿单链表的插入操作为例来给你分析一下。
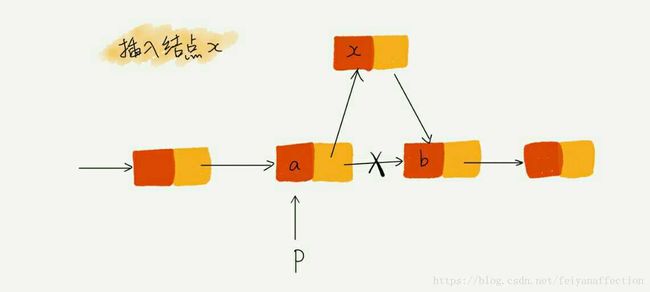
如图所示,我们希望在结点 a 和相邻的结点 b 之间插入结点 x,假设当前指针 p 指向结点 a。如果我们将代码实现变成下面这个样子,就会发生指针丢失和内存泄露。
p->next = x; // 将 p 的 next 指针指向 x 结点;
x->next = p->next; // 将 x 的结点的 next 指针指向 b 结点;
初学者经常会在这儿犯错。p->next指针在完成第一步操作之后,已经不再指向结点 b 了,而是指向结点 x。第 2 行代码相当于将 x 赋值给 x->next,自己指向自己。因此,整个链表也就断成了两半,从结点 b 往后的所有结点都无法访问到了。
对于有些语言来说,比如 C 语言,内存管理是由程序员负责的,如果没有手动释放结点对应的内存空间,就会产生内存泄露。所以,我们插入结点时,一定要注意操作的顺序,要先将结点 x 的 next 指针指向结点 b,再把结点 a 的 next 指针指向结点 x,这样才不会丢失指针,导致内存泄漏。所以,对于刚刚的插入代码,我们只需要把第 1 行和第 2 行代码的顺序颠倒一下就可以了。
同理,删除链表结点时,也一定要记得手动释放内存空间,否则,也会出现内存泄漏的问题。当然,对于像 Java 这种虚拟机自动管理内存的编程语言来说,就不需要考虑这么多了。
技巧三:利用哨兵简化实现难度
首先,我们先来回顾一下单链表的插入和删除操作。如果我们在结点 p 后面插入一个新的结点,只需要下面两行代码就可以搞定。
new_node->next = p->next;
p->next = new_node;
但是,当我们要向一个空链表中插入第一个结点,刚刚的逻辑就不能用了。我们需要进行下面这样的特殊处理,其中 head 表示链表的头结点。所以,从这段代码,我们可以发现,对于单链表的插入操作,第一个结点和其他结点的插入逻辑是不一样的。
if (head == null) {
head = new_node;
}
我们再来看单链表结点删除操作。如果要删除结点 p 的后继结点,我们只需要一行代码就可以搞定。
p->next = p->next->next;
但是,如果我们要删除链表中的最后一个结点,前面的删除代码就不 work 了。跟插入类似,我们也需要对于这种情况特殊处理。写成代码是这样子的:
if (head->next == null) {
head = null;
}
从前面的一步一步分析,我们可以看出,针对链表的插入、删除操作,需要对插入第一个结点和删除最后一个结点的情况进行特殊处理。这样代码实现起来就会很繁琐,不简洁,而且也容易因为考虑不全而出错。如何来解决这个问题呢?
技巧三中提到的哨兵就要登场了。哨兵,解决的是国家之间的边界问题。同理,这里说的哨兵也是解决“边界问题”的,不直接参与业务逻辑。
还记得如何表示一个空链表吗?head=null 表示链表中没有结点了。其中 head 表示头结点指针,指向链表中的第一个结点。
如果我们引入哨兵结点,在任何时候,不管链表是不是空,head 指针都会一直指向这个哨兵结点。我们也把这种有哨兵结点的链表叫带头链表。相反,没有哨兵结点的链表就叫作不带头链表。
我画了一个带头链表,你可以发现,哨兵结点是不存储数据的。因为哨兵结点一直存在,所以插入第一个结点和插入其他结点,删除最后一个结点和删除其他结点,都可以统一为相同的代码实现逻辑了。
实际上,这种利用哨兵简化编程难度的技巧,在很多代码实现中都有用到,比如插入排序、归并排序、动态规划等。这些内容我们后面才会讲,现在为了让你感受更深,我再举一个非常简单的例子。代码我是用 C 语言实现的,不涉及语言方面的高级语法,很容易看懂,你可以类比到你熟悉的语言
代码一:
int find(char* a, int n, char key) {
int i = 0;
while (i < n) {
if (a[i] == key) {
return i;
}
++i;
}
return -1;
}
代码二:
inf find(char* a, int n, int key) {
if (a[n-1] == key) {
return n-1;
}
char tmp = a[n-1];
a[n-1] = key;
int i = 0;
while (a[i] != key) {
++i;
}
a[n-1] = tmp;
if (i == n-1) return -1;
return i;
}
对比两段代码,在字符串 a 很长的时候,比如几万、几十万,你觉得哪段代码运行得更快点呢?答案是代码二,因为两段代码中执行次数最多就是 while 循环那一部分。第二段代码中,我们通过一个哨兵 a[n-1] = key,成功省掉了一个比较语句 i 当然,这只是为了举例说明哨兵的作用,你写代码的时候千万不要写第二段那样的代码,因为可读性太差了。大部分情况下,我们并不需要如此追求极致的性能。 技巧四:重点留意边界条件处理 我经常用来检查链表代码是否正确的边界条件有这样几个: (1) 如果链表为空时,代码是否能正常工作? (2) 如果链表只包含一个结点时,代码是否能正常工作? (3) 如果链表只包含两个结点时,代码是否能正常工作? (4) 代码逻辑在处理头结点和尾结点的时候,是否能正常工作? 当你写完链表代码之后,除了看下你写的代码在正常的情况下能否工作,还要看下在上面我列举的几个边界条件下,代码仍然能否正确工作。如果这些边界条件下都没有问题,那基本上可以认为没有问题了。 当然,边界条件不止我列举的那些。针对不同的场景,可能还有特定的边界条件,这个需要你自己去思考,不过套路都是一样的。 实际上,不光光是写链表代码,你在写任何代码时,也千万不要只是实现业务正常情况下的功能就好了,一定要多想想,你的代码在运行的时候,可能会遇到哪些边界情况或者异常情况。遇到了应该如何应对,这样写出来的代码才够健壮! 技巧五:举例画图,辅助思考 你可以找一个具体的例子,把它画在纸上,释放一些脑容量,留更多的给逻辑思考,这样就会感觉到思路清晰很多。比如往单链表中插入一个数据这样一个操作,我一般都是把各种情况都举一个例子,画出插入前和插入后的链表变化,如图所示: 看图写代码,是不是就简单多啦?而且,当我们写完代码之后,也可以举几个例子,画在纸上,照着代码走一遍,很容易就能发现代码中的 Bug。 技巧六:多写多练,没有捷径 现在我写这些代码,简直就和“玩儿”一样,其实也没有什么技巧,就是把常见的链表操作都自己多写几遍,出问题就一点一点调试,熟能生巧! 所以,我精选了 5 个常见的链表操作。你只要把这几个操作都能写熟练,不熟就多写几遍,我保证你之后再也不会害怕写链表代码。 (1)单链表反转 (2)链表中环的检测 (3)两个有序的链表合并 (4)删除链表倒数第 n 个结点 (5)求链表的中间结点 这节我主要和你讲了写出正确链表代码的六个技巧。分别是理解指针或引用的含义、警惕指针丢失和内存泄漏、利用哨兵简化实现难度、重点留意边界条件处理,以及举例画图、辅助思考,还有多写多练。 我觉得,写链表代码是最考验逻辑思维能力的。因为,链表代码到处都是指针的操作、边界条件的处理,稍有不慎就容易产生 Bug。链表代码写得好坏,可以看出一个人写代码是否够细心,考虑问题是否全面,思维是否缜密。所以,这也是很多面试官喜欢让人手写链表代码的原因。所以,这一节讲到的东西,你一定要自己写代码实现一下,才有效果。 今天我们讲到用哨兵来简化编码实现,你是否还能够想到其他场景,利用哨兵可以大大地简化编码难度? 1.含义:将某个变量(对象)赋值给指针(引用),实际上就是就是将这个变量(对象)的地址赋值给指针(引用)。 1.插入节点 1.什么是“哨兵”? 经常用来检查链表是否正确的边界4个边界条件: 核心思想:释放脑容量,留更多的给逻辑思考,这样就会感觉到思路清晰很多。 5个常见的链表操作: 附上实现: C++实现: 结果:
软件开发中,代码在一些边界或者异常情况下,最容易产生 Bug。链表代码也不例外。要实现没有 Bug 的链表代码,一定要在编写的过程中以及编写完成之后,检查边界条件是否考虑全面,以及代码在边界条件下是否能正确运行。
对于稍微复杂的链表操作,比如前面我们提到的单链表反转,指针一会儿指这,一会儿指那,一会儿就被绕晕了。总感觉脑容量不够,想不清楚。所以这个时候就要使用大招了,举例法和画图法。
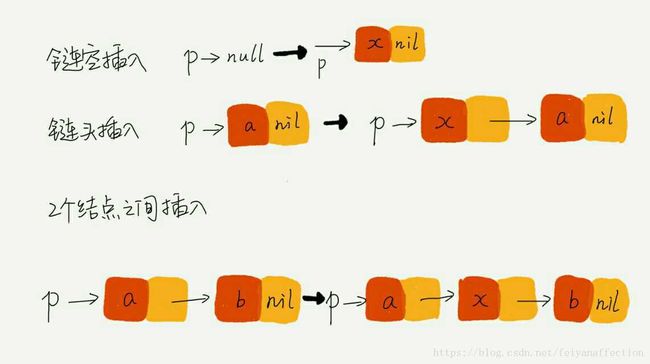
如果你已经理解并掌握了我前面所讲的方法,但是手写链表代码还是会出现各种各样的错误,也不要着急。因为我最开始学的时候,这种状况也持续了一段时间。内容小结:
课后思考?
1.小结:
一、理解指针或引用的含义
2.示例:
p—>next = q; 表示p节点的后继指针存储了q节点的内存地址。
p—>next = p—>next—>next; 表示p节点的后继指针存储了p节点的下下个节点的内存地址。二、警惕指针丢失和内存泄漏(单链表)
在节点a和节点b之间插入节点x,b是a的下一节点,,p指针指向节点a,则造成指针丢失和内存泄漏的代码:p—>next = x;x—>next = p—>next; 显然这会导致x节点的后继指针指向自身。
正确的写法是2句代码交换顺序,即:x—>next = p—>next; p—>next = x;
2.删除节点
在节点a和节点b之间删除节点b,b是a的下一节点,p指针指向节点a:p—>next = p—>next—>next;三、利用“哨兵”简化实现难度
链表中的“哨兵”节点是解决边界问题的,不参与业务逻辑。如果我们引入“哨兵”节点,则不管链表是否为空,head指针都会指向这个“哨兵”节点。我们把这种有“哨兵”节点的链表称为带头链表,相反,没有“哨兵”节点的链表就称为不带头链表。
2.未引入“哨兵”的情况
如果在p节点后插入一个节点,只需2行代码即可搞定:
new_node—>next = p—>next;
p—>next = new_node;
但,若向空链表中插入一个节点,则代码如下:
if(head == null){
head = new_node;
}
如果要删除节点p的后继节点,只需1行代码即可搞定:
p—>next = p—>next—>next;
但,若是删除链表的最有一个节点(链表中只剩下这个节点),则代码如下:
if(head—>next == null){
head = null;
}
从上面的情况可以看出,针对链表的插入、删除操作,需要对插入第一个节点和删除最后一个节点的情况进行特殊处理。这样代码就会显得很繁琐,所以引入“哨兵”节点来解决这个问题。
3.引入“哨兵”的情况
“哨兵”节点不存储数据,无论链表是否为空,head指针都会指向它,作为链表的头结点始终存在。这样,插入第一个节点和插入其他节点,删除最后一个节点和删除其他节点都可以统一为相同的代码实现逻辑了。
4.“哨兵”还有哪些应用场景?
这个知识有限,暂时想不出来呀!但总结起来,哨兵最大的作用就是简化边界条件的处理。四、重点留意边界条件处理
1.如果链表为空时,代码是否能正常工作?
2.如果链表只包含一个节点时,代码是否能正常工作?
3.如果链表只包含两个节点时,代码是否能正常工作?
4.代码逻辑在处理头尾节点时是否能正常工作?五、举例画图,辅助思考
六、多写多练,没有捷径
1.单链表反转
2.链表中环的检测
3.两个有序链表合并
4.删除链表倒数第n个节点
5.求链表的中间节点package linkedlist;
/**
* 1) 单链表反转
* 2) 链表中环的检测
* 3) 两个有序的链表合并
* 4) 删除链表倒数第n个结点
* 5) 求链表的中间结点
*/
public class LinkedListAlgo {
// 单链表反转
public static Node reverse(Node list) {
Node headNode = null;
Node previousNode = null;
Node currentNode = list;
while (currentNode != null) {
Node nextNode = currentNode.next;
if (nextNode == null) {
headNode = currentNode;
}
currentNode.next = previousNode;
previousNode = currentNode;
currentNode = nextNode;
}
return headNode;
}
// 检测环
public static boolean checkCircle(Node list) {
if (list == null) return false;
Node fast = list.next;
Node slow = list;
while (fast != null && fast.next != null) {
fast = fast.next.next;
slow = slow.next;
if (slow == fast) {
return true;
}
}
return false;
}
// 有序链表合并
public static Node mergeSortedLists(Node la, Node lb) {
if (la == null) return lb;
if (lb == null) return la;
Node p = la;
Node q = lb;
Node head;
if (p.data < q.data) {
head = p;
p = p.next;
} else {
head = q;
q = q.next;
}
Node r = head;
while (p != null && q != null) {
if (p.data < q.data) {
r.next = p;
p = p.next;
} else {
r.next = q;
q = q.next;
}
r = r.next;
}
if (p != null) {
r.next = p;
} else {
r.next = q;
}
return head;
}
// 删除倒数第K个结点
public static Node deleteLastKth(Node list, int k) {
Node fast = list;
int i = 1;
while (fast != null && i < k) {
fast = fast.next;
++i;
}
if (fast == null) return list;
Node slow = list;
Node prev = null;
while (fast.next != null) {
fast = fast.next;
prev = slow;
slow = slow.next;
}
if (prev == null) {
list = list.next;
} else {
prev.next = prev.next.next;
}
return list;
}
// 求中间结点
public static Node findMiddleNode(Node list) {
if (list == null) return null;
Node fast = list;
Node slow = list;
while (fast.next != null && fast.next.next != null) {
fast = fast.next.next;
slow = slow.next;
}
return slow;
}
public static void printAll(Node list) {
Node p = list;
while (p != null) {
System.out.print(p.data + " ");
p = p.next;
}
System.out.println();
}
public static Node createNode(int value) {
return new Node(value, null);
}
public static class Node {
private int data;
private Node next;
public Node(int data, Node next) {
this.data = data;
this.next = next;
}
public int getData() {
return data;
}
}
}
LinkedList.h#ifndef ALGORITHMHUB_LINKEDLIST_H
#define ALGORITHMHUB_LINKEDLIST_H
#include #include 0 0 1 2 3 4 5 6 7 8 9
9 8 7 6 5 4 3 2 1 0
0
5