十大经典排序算法（希尔排序、堆排序、计数排序、桶排序和基数排序）

十大经典排序算法一（冒泡排序、选择排序、插入排序、快速排序、归并排序）

希尔排序

希尔排序原理

希尔排序是插入排序的一种，他是针对直接插入排序算法的改进，由D.L.Shell于1959年提出而得名。

希尔排序的基本思想是把待排序的数列分为多个组，然后在对每个组进行插入排序，先让数列整体大致有序，然后多次调整分组方式，使的数列更加有序，最后再使用一次插入排序，整个数列将全部有序。

希尔排序代码实现

#include 
#include 
//对希尔排序中的单个组进行排序。
//arr-待排序的数组，len-数组总的长度，ipos-分组的起始位置，istep-分组的步长（增量）。
void groupsort(int *arr, int len, int ipos,int istep)
{
    for (int i = ipos+istep; i < len ; i+=istep) {
        int tmp = arr[i],j;
        for(j = i - istep;j>=0&&tmp<arr[j];j-=istep){
            arr[j+istep] = arr[j];
        }
        arr[j+istep] = tmp;
    }
}
// 希尔排序，arr是待排序数组的首地址，len是数组的大小。
void shellsort(int *arr,unsigned int len)
{
    for(int i = len/2;i>0;i/=2){
        for (int j = 0; j < i; ++j) {
            groupsort(arr,len,j,i);
        }
    }
}
int main(int argc,char *argv[])
{
    int arr[]={44,3,38,5,47,15,36,26,27,2,46,4,19,50,48};
    int len=sizeof(arr)/sizeof(int);
    shellsort(arr,len);  
 // 调用插入排序函数对数组排序。
    // 显示排序结果。
    int yy; for (yy=0;yy<len;yy++) printf("%2d ",arr[yy]); printf("\n");
    // system("pause");  // widnows下的C启用本行代码。
    return 0;
}

堆排序

堆排序原理

堆排序是利用堆这种数据结构而设计的一种排序算法，堆具有以下特点：

1. 完全二叉树；(从上到下，从左到右，每一层的结点都是满的，最下一层所有的结点都连续集中在最左边)
2. 二叉树每个节点的值都大或等于其左右子树结点的值称为大顶堆；或每个结点的值都小于或等于左右子树的值，称为小顶堆；

将完全二叉树按如下方式编号，则该堆可以对应一个数组；且左右结点和父子结点之间有以下对应关系。

堆排序代码实现

#include 
#include 

// 交换两个元素的值。
void swap(int *a,int *b) { int temp=*b; *b=*a; *a=temp; }

// 采用循环实现heapify（元素下沉）。
// arr-待排序数组的地址，start-待heapify节点的下标，end-待排序数组最后一个元素的下标。
void heapify(int *arr,int start,int end)
{
    int dad = start;
    int son = start * 2 + 1;
    while(son <= end){
        if(son + 1<= end && arr[son] < arr[son+1]) son++;
        if(arr[dad] > arr[son]) return ;
        swap(&(arr[dad]),&(arr[son]));
        dad = son;
        son = dad * 2 +1;
    }
}

// 采用递归实现heapify。
void heapify1(int *arr,int start,int end)
{
   int dad = start;
   int son = dad*2 +1;
   if(son > end) return;
   if(son + 1 <= end && arr[son] < arr[son+1] ) son++;
   if(arr[son] < arr[dad]) return;
   swap(&arr[son],&arr[dad]);
   heapify1(arr,son,end);
}
void heapsort(int *arr, int len)
{
    for(int i = (len - 1)/2;i>=0;i--){
        heapify(arr,i,len -1);
    }
    for(int i = len - 1;i>0;i--){
        swap(&arr[0],&arr[i]);
        heapify(arr,0,i-1);
    }
}

int main()
{
  int arr[]={44,3,38,5,47,15,36,26,27,2,46,4,19,50,48};

  int len=sizeof(arr)/sizeof(int);

  heapsort(arr,len);

  // 显示排序结果。
  int yy; for (yy=0;yy<len;yy++) printf("%2d ",arr[yy]); printf("\n");



  return 0;
}

计数排序

计数排序算法的时间复杂度降低到O(n+k),但是有两个要满足的前提：

1. 需要排序元素必须是整数；
2. 排序元素的取值要在一定范围内，并且比较集中，只有满足这两个条件，才可最大程度发挥计数排序优势。

计数排序代码实现

#include 
#include 
#include 

// 获取待排序数组的最大元素的值。
int arrmax(int *arr,unsigned int len)
{
    int tmp = arr[0];
    for(int i = 1;i<len ;i++){
        if(arr[i] > tmp) tmp = arr[i];
    }
    return tmp;
}

// 计数排序主函数，arr-待排序数组的地址，len-数组的长度。
void countsort(int *arr,unsigned int len)
{
    if(len < 2 ) return ;
    int max = arrmax(arr,len);
    int tmp[max + 1];
    memset(tmp,0,sizeof (tmp));
    for(int i = 0;i<len ;i++){
        tmp[arr[i]]++;
    }
    int index = 0;
    for(int i = 1;i<max+1;i++){
        for(int j =0;j<tmp[i];j++){
        arr[index++]  = i;
        }
    }
}

int main()
{
    int arr[]={2,3,8,7,1,2,2,2,7,3,9,8,2,1,4,2,4,6,9,2};

    int len=sizeof(arr)/sizeof(int);

    int xx; for (xx=0;xx<len;xx++) printf("%2d ",arr[xx]); printf("\n");

    countsort(arr,len);

    // 显示排序结果。
    int yy; for (yy=0;yy<len;yy++) printf("%2d ",arr[yy]); printf("\n");

    // system("pause");  // widnows下的C启用本行代码。

    return 0;
}

计数排序的优化

可以一次性计算出最大值和最小值，然后计算差值，确定所需辅助数组的大小；
记数排序的缺陷是空间消耗较多，排序的时候可以将数组的大小开为max-min+1;比如高考成绩的排名可以用记数排序

桶排序

桶排序原理

假设输入数据服从均匀分布，将数据分到有限数量的桶里，然后再对每个桶分别排序，最后把全部的桶数据合并。

桶排序的时间复杂度，取决于对各个桶之间数据进行排序的时间复杂度，因为其它部分的时间复杂度都为O(n).很显然，桶划分的越小各个桶之间数据越少，排序所用的时间也会越少，但相应的空间消耗会增大。

重点理解桶排序的思想，在现实世界中，大部分的数据分布是均匀的，或者在设计的时候让他均匀分布，或者转换为均匀分布。既然数据均匀分布了，桶排序的效率就能发挥出来。

理解桶排序的思想可以设计出很高效的算法。（分库分表）

桶排序代码实现

#include 
#include 
#include 

// 采用两层循环实现冒泡排序的方法。
// 参数arr是待排序数组的首地址，len是数组元素的个数。
void bubblesort(int *arr,unsigned int len)
{
    if (len<2) return; // 数组小于2个元素不需要排序。

    int ii;    // 排序的趟数的计数器。
    int jj;    // 每趟排序的元素位置计数器。
    int itmp;  // 比较两个元素大小时交换位置用到的临时变量。

    // 44,3,38,5,47,15,36,26,27,2,46,4,19,50,48
    for (ii=len-1;ii>0;ii--)  // 一共进行len-1趟比较。
    {
        for (jj=0;jj<ii;jj++)  // 每趟只需要比较0......ii之间的元素，ii之后的元素是已经排序好的。
        {
            if (arr[jj]>arr[jj+1])  // 如果前面的元素大于后面的元素，则交换它位的位置。
            {
                itmp=arr[jj+1];
                arr[jj+1]=arr[jj];
                arr[jj]=itmp;
            }
        }
    }
}

// 桶排序主函数，参数arr是待排序数组的首地址，len是数组元素的个数。
void bucketsort(int *arr,unsigned int len)
{
    int buckets[5][5];   // 分配五个桶。
    int bucketssize[5];  // 每个桶中元素个数的计数器。

    // 初始化桶和桶计数器。
    memset(buckets,0,sizeof(buckets));
    memset(bucketssize,0,sizeof(bucketssize));

    // 把数组arr的数据放入桶中。
    int ii=0;
    for (ii=0;ii<len;ii++)
    {
        buckets[arr[ii]/10][bucketssize[arr[ii]/10]++]=arr[ii];
    }

    // 对每个桶进行冒泡排序。
    for (ii=0;ii<5;ii++)
    {
        bubblesort(buckets[ii],bucketssize[ii]);
    }

    // 把每个桶中的数据填充到数组arr中。
    int jj=0,kk=0;
    for (ii=0;ii<5;ii++)
    {
        for (jj=0;jj<bucketssize[ii];jj++)
            arr[kk++]=buckets[ii][jj];
    }
}

int main(int argc,char *argv[])
{
    int arr[]={21,3,30,44,15,36,6,10,9,19,25,48,5,23,47};
    int len=sizeof(arr)/sizeof(int);

    int xx; for (xx=0;xx<len;xx++) printf("%2d ",arr[xx]); printf("\n");

    bucketsort(arr,len);

    // 显示排序结果。
    int ii; for (ii=0;ii<len;ii++) printf("%2d ",arr[ii]); printf("\n");

    
    return 0;
}

基数排序

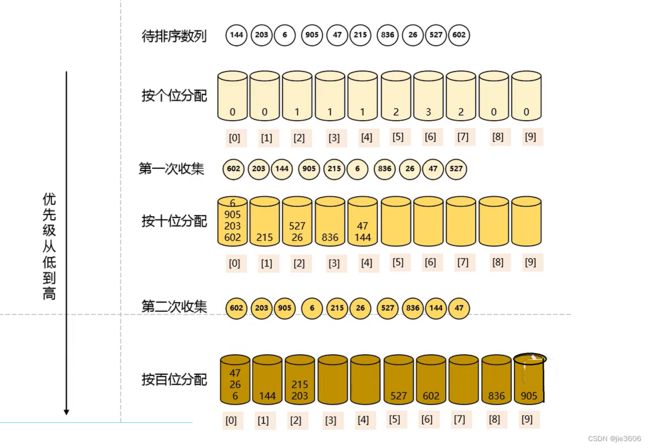
基数排序是桶排序的扩展，他的基本思想是：将整数按位切割成不同的数字，然后按每个位分别比较。

具体做法是：将所有带比较数值统一为同样的数位长度，数位较短的数前面补0.然后，从最底位开始，依次进行排序。这样从最低位排序一直到最高位排序完成后，就变成了一个有序数列。

基数排序原理

基数排序代码实现

#include 
#include 
#include 

// 获取数组arr中最大值，arr-待排序的数组，len-数组arr的长度。
int arrmax(int *arr,unsigned int len)
{
  int ii,imax;

  imax=arr[0];

  for (ii=1;ii<len;ii++)
    if (arr[ii]>imax) imax=arr[ii];

  return imax;
}

// 对数组arr按指数位进行排序。
// arr-待排序的数组，len-数组arr的长度。
// exp-排序指数，exp=1：按个位排序；exp=10：按十位排序；......
void _radixsort(int *arr,unsigned int len,unsigned int exp)
{
  int ii;
  int result[len];       // 存放从桶中收集后数据的临时数组。
  int buckets[10]={0};   // 初始化10个桶。

  // 遍历arr，将数据出现的次数存储在buckets中。
  for (ii=0;ii<len;ii++)
    buckets[(arr[ii]/exp)%10]++;

  // 调整buckets各元素的值，调整后的值就是arr中元素在result中的位置。
  for (ii=1;ii<10;ii++)
    buckets[ii]=buckets[ii]+buckets[ii-1];

  // 将arr中的元素填充到result中。
  for (ii=len-1;ii>=0;ii--)
  {
    int iexp=(arr[ii]/exp)%10;
    result[buckets[iexp]-1]=arr[ii];
    buckets[iexp]--;
  }
  
  // 将排序好的数组result复制到数组arr中。
  memcpy(arr,result,len*sizeof(int));
}

// 基数排序主函数，arr-待排序的数组，len-数组arr的长度。
void radixsort(int *arr,unsigned int len)
{
  int imax=arrmax(arr,len);    // 获取数组arr中的最大值。

  int iexp;    // 排序指数，iexp=1：按个位排序；iexp=10：按十位排序；......

  // 从个位开始，对数组arr按指数位进行排序。
  for (iexp=1;imax/iexp>0;iexp=iexp*10)
  {
    _radixsort(arr,len,iexp);
    int yy; printf("exp=%-5d  ",iexp); for (yy=0;yy<len;yy++) printf("%2d ",arr[yy]); printf("\n");
  }
}

int main(int argc,char *argv[])
{
  int arr[]={144,203,738,905,347,215,836,26,527,602,946,504,219,750,848};
  int len=sizeof(arr)/sizeof(int);

  radixsort(arr,len);  // 基数排序。

  // 显示排序结果。
  int yy; for (yy=0;yy<len;yy++) printf("%2d ",arr[yy]); printf("\n");

  // system("pause");  // widnows下的C启用本行代码。

  return 0;
}

基数排序的应用

由于整数也可以表达字符串（比如名字或日期）和特定格式的浮点数，所以基数排序也是用于其它数据类型。

例如：按照出生日期排序，先按照日把数据放到桶中，再按月份，最后按照年放入桶中；