机器学习(一) —— 机器学习基础

机器学习(一) —— 机器学习基础

大家可以关注知乎或微信公众号的share16，我们也会同步更新此文章。

   写在前面的话
   这是我第一次接触机器学习，本文记录了机器学习的基础知识和相关代码，以供参考。

   机器学习是从数据中自动分析获得模型/规律，并利用模型对未知数据进行预测；在机器学习中算法是核心，数据是计算的基础。

   大部分复杂模型的算法设计都是算法工程师(博士/硕士)在做，而我们只需：1︎⃣学会分析问题，使用机器学习相关算法完成对应的需求；2︎⃣掌握算法的基本思想，学会对不同问题选择对应的算法解决；3︎⃣学会利用框架和库解决问题；

   scikit-learn包含众多顶级机器学习算法，主要有六大类的基本功能-分别是分类、回归、聚类、数据降维、模型选择和数据预处理。

     注：变量按其数值表现是否连续，可分为连续变量和离散变量。
     连续变量与离散变量的简单区别方法：
     连续变量是一直叠加上去的，增长量可以划分为固定的单位，即1,2,3…   如：一个人的身高，他首先长到1.51，然后才能长到1.52，1.53……
     离散变量则是通过计数方式取得的，即对所要统计的对象进行计数，增长量非固定的，如：一个地区的企业数目可以是今年只有一家，而第二年开了十家；一个企业的职工人数今年只有10人，第二年一次招聘了20人等。

一、数据集

1.1 加载数据集

   数据集的采集：公司内部产生的数据、和其他公司合作获取的数据、购买的数据等；

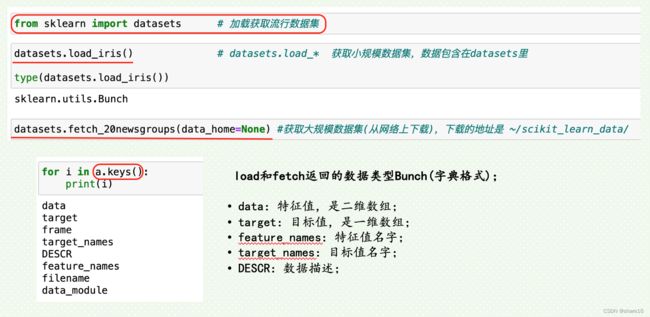
sklearn.datasets.load_iris()

sklearn.datasets.fetch_20newsgroups(data_home=None,···)

1.2 划分数据集

   数据的基本处理：数据清洗、合并、级联等；

   机器学习的数据集，一般会分为两个部分(训练集和测试集)，如下：
sklearn.model_selection.train_test_split(x, [y], test_size, train_size, random_state, shuffle, stratify)

• 训练集：用于训练，构建模型；测试集：在模型检验时使用，用于评估模型是否有效；
• test_size/train_size：默认None，若是float([0,1])，代表其在数据集中所占的比例；若是int，代表样本的绝对数量；
• random_state：随机数种子，不同的种子会造成不同的随机采样结果(相同的种子采样结果相同)；
• shuffle：表示是否打乱数据位置，True或False，默认True；
• stratify：表示是否按照样本比例(不同类别的比例)来划分数据集，如原始数据集 类A:类B = 75%:25%，那么划分的测试集和训练集中的A:B的比例都会是75%:25%；可用于样本类别差异很大的情况，一般使用为：stratify=y，即用数据集的标签y来进行划分；
  
  

二、特征工程

   特征工程是使用专业背景知识和技巧处理数据，使得特征能在机器学习算法上发挥更好的作用的过程；其会直接影响机器学习的效果。特征工程包含的内容：特征预处理、特征降维、特征提取。

2.1 特征预处理(归一化/标准化)

归一化：通过对原始数据进行变换把数据映射到[0,1]之间，$y=\frac{x-min}{max-min}$ 。

标准化：通过对原始数据进行变换把数据变换到均值为0、标准差为1的范围内，$y=\frac{x-\mu }{\sigma }$ 。

将 标签 编码为 分类变量：pd.factorize、sklearn.LabelEncoder；

将 分类变量 编码为 虚拟指标变量：pd.get_dummies、sklearn.OneHotEncoder；
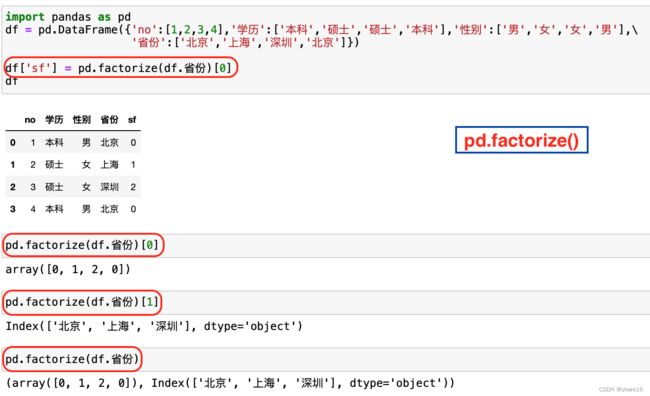
哑变量编码：即pd.get_dummies，数据集中存在某n列的值为字符串类型，如学历、性别等；可利用此函数进行转换，如下。

''' 归一化：将数据缩放到给定范围内，feature_range默认范围是(0,1) '''
MinMaxScaler = sklearn.preprocessing.MinMaxScaler(feature_range=(0,1))
MinMaxScaler.fit_transform(array).round(2)

''' 标准化 '''
StandardScaler = sklearn.preprocessing.StandardScaler()
StandardScaler.fit_transform(array).round(2)

''' 标签编码为分类变量 '''
x,y = pd.factorize(df.省份)

''' 哑变量编码 '''
pd.get_dummies(df,columns=['学历','性别','省份'])
pd.get_dummies(df[['学历','性别']])

2.2 特征降维(特征选择/主成分分析/线性判别器)

   降维是指在某些限定条件下，降低随机变量(特征)个数，得到一组‘不相关’主变量的过程。

• 降低随机变量的个数；
• 相关特征(correlated feature)，如：相对湿度与降雨量之间的相关等等；

降维方法：特征选择、单变量特征选定、递归特征消除、主成分分析、线性判别器

特征选择：数据中包含冗余或无关变量(或称特征、属性、指标等)，旨在从原有特征中找出主要特征。

• Filter(过滤式)：主要探究特征本身特点、特征与特征和目标值之间的关联(方差选择法:低方差特征过滤；皮尔逊相关系数)；
• Embedded(嵌入式)：算法自动选择特征，即特征与目标值之间的关联(决策树:信息熵、信息增益；正则化:L1、L2；深度学习:卷积等)；

单变量特征选定：分析选择对结果影响最大的数据特征。如卡方检验，其是统计样本实际值与预测值之间的偏离程度，偏离程度决定了卡方值的大小(卡方值越大，两者越不符合；卡方值越小，两者越符合；若两者相等，卡方值等于0，表明预测值完全符合)。

递归特征消除：使用一个基模型进行多轮训练，每轮训练后消除若干权值系数的特征，再基于新的特征集进行下一轮训练。通过每一个基模型的精度，找到对最终的预测结果影响最大的数据特征。

主成分分析PCA：是一种无监督的降维方法；是一种利用正交变换，把由线性相关变量表示的观测数据转化为少数几个由线性无关变量表示的数据；新变量可能是正交变换中变量的方差最大的，方差表示在新变量上信息的大小，将变量依次成为第一主成分、第二主成分。

线性判别器LDA：是一种有监督的降维方法；LDA与PCA相似的地方在于都是降维方法，参考的都是方差。LDA的降维是：在投影之后，同类别的数据内方差尽可能小，不同类别之间的方差尽可能大。若将所有样本的X(特征)投影在同一条直线的话，那么就是label相同的数据投影结果应该很接近，反之label不一样的数据投影结果应该远一点。

''' 过滤式：删除方差低于threshold的特征 ''' 
VarianceThreshold = feature_selection.VarianceThreshold(threshold=0.0)
VarianceThreshold.fit_transform(array)

''' 皮尔逊相关系数 ''' 
from scipy import stats
stats.pearsonr(x,y) # x/y均是一位数组

''' 主成分分析PCA
n_components是float，则表示保留百分之多少的信息；
n_components是int，则表示减少到多少特征；''' 
PCA = sklearn.decomposition.PCA(n_components=None)
PCA.fit_transform(array)

''' 线性判别器LDA ''' 
from sklearn.discriminant_analysis import\
LinearDiscriminantAnalysis as LDA 
lda = LDA(n_components=None)

2.3 特征提取(字典/文本特征提取)

特征提取：是将任意数据(如文本或图像)转换为可用于机器学习的数字特征。
字典特征提取：对字典数据进行特征值化；
文本特征提取：对文本数据进行特征值化；
Tf-idf文本特征提取：用以评估一字词对于一个文件集或语料库中的一份文件的重要程度(词频(tf)是指某一给定词语在该文件中出现的频率；逆向文档频率(idf)是一个词语普遍重要性的度量，即某一特定词语的idf，可由总文件数目除以包含该词语之文件的数目，再将得到的商取以10为底的对数得到；某特定词语的重要程度等于该词的tf*idf)；
图像特征提取；

''' 字典特征提取：sparse-默认True，即变换是否产生scipy.sparse矩阵 '''
DictVectorizer = feature_extraction.DictVectorizer(sparse=False)
# 返回sparse矩阵
DictVectorizer.fit_transform(字典组成的列表)
# 返回转换之前数据格式
DictVectorizer.inverse_transform(array或sparse矩阵)
# 返回类别名称
DictVectorizer.get_feature_names()

''' 文本特征提取：变换是否产生scipy.sparse矩阵 '''
CountVectorizer = feature_extraction.text.CountVectorizer(encoding,stop_words,analyzer)
# 返回单词列表
CountVectorizer.get_feature_names()
# 返回sparse矩阵
CountVectorizer.fit_transform(文本或文本组成的列表).toarray()
# 返回转换之前数据格式
CountVectorizer.inverse_transform(array或sparse矩阵)

''' Tf-idf文本特征提取 '''
TfidfVectorizer = feature_extraction.text.TfidfVectorizer()
TfidfVectorizer.fit_transform(文本或文本组成的列表).toarray()

''' jieba分词处理 '''
jieba.lcut(文本)

三、分类算法

3.1 K 近邻算法

   K 近邻算法(K-Nearest Neighbors,KNN)是一种惰性学习算法，可用于回归和分类，它的主要思想是物以类聚，人以群分；对于一个新的实例，我们在有标签的训练集上找到与其最相近的k个数据，用他们的label进行投票，分类问题则进行表决投票，回归问题使用加权平均或直接平均的方法。 KNN算法中，最需要关注三个问题：k值的选择、距离的计算和决策规则。

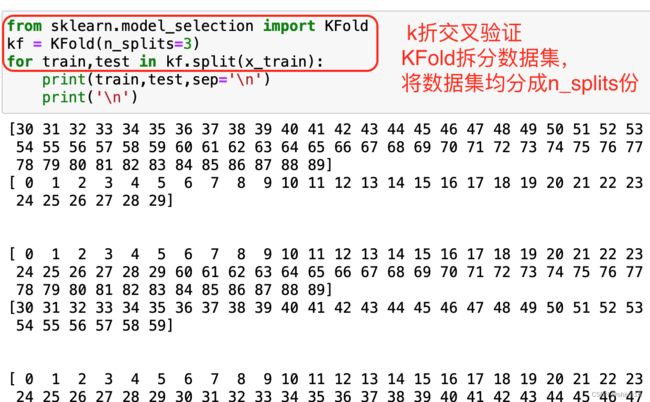
• k值的选取：根据交叉检验法选取，详见下图；
• 距离的计算：两样本间的距离，方法有欧式距离、曼哈顿距离等；
  • 曼哈顿距离：$|a_1-b_1|+|a_2-b_2|+\cdot \cdot \cdot +|a_n-b_n|$；
  • 欧氏距离：$\sqrt{(a_1-b_1{)}^2+(a_2-b_2{)}^2+\cdot \cdot \cdot +(a_n-b_n{)}^2}$；
• 决策规则：分类用众数，回归用平均值。有时也要考虑到距离因素，给距离越近的样本加点权重；

''' 分类 '''
from sklearn.neighbors import KNeighborsClassifier 
knn = KNeighborsClassifier(n_neighbors=1)
knn.fit(data,target)   # 利用模型对数据进行拟合
knn.score(data,target) # 打印模型的得分
knn.predict(X_new)     # 进行预测，X_new新数据点

''' 回归 '''
from sklearn.neighbors import KNeighborsRegressor
KNeighborsRegressor(n_neighbors=1)

• n_neighbors：KNN中的k值，即选取邻居的数量，默认5； weights：权重，默认uniform(统一的权重，即每个邻域中的所有点权重相等)；
• 欧式距离：即 metric=minkowski & p=2 ；
• algorithm：用于计算最近邻居的算法，默认auto，还可取值ball_tree、kd_tree、brute；
  
  

3.2 朴素贝叶斯算法

   朴素贝叶斯算法是一种基于贝叶斯理论的有监督学习算法，之所以说‘朴素’，是因为这个算法是基于样本特征之间互相独立的朴素假设。

联合概率：包含多个条件，且所有条件同时成立的概率，记作P(A,B)；
$P(A,B)=P(A)P(B)$

条件概率：指事件A在另外一个事件B已经发生条件下的发生概率，记作P(A|B)；
$P(A|B)=\frac{P(AB)}{P(B)}$
$P(A_1,A_2|B)=P(A_1|B)P(A_2|B)$ (注意：A₁,A₂相互独立)

贝叶斯公式：$P(B|A)=\frac{P(A,B)}{P(A)}=\frac{P(A|B)P(B)}{P(A)}$

''' 二项分布：伯努利朴素贝叶斯(alpha:平滑参数,默认1.0,0表示不平滑) '''
from sklearn.naive_bayes import BernoulliNB
clf = BernoulliNB(alpha=1.0)
clf.fit(X,Y)             # 拟合
clf.score(X,Y)           # 得分
clf.predict(X_new)       # 预测
clf.predict_proba(X_new) # 模型预测分类的概率 

''' 正态分布：高斯朴素贝叶斯 '''
from sklearn.naive_bayes import GaussianNB

''' 多项式朴素贝叶斯 '''
from sklearn.naive_bayes import MultinomialNB

3.3 决策树与随机森林

   决策树是一种在分类与回归中都有非常广泛应用的算法，它的原理是通过对一系列问题进行if-else的推导，最终实现决策；但其容易出现过拟合问题。

   随机森林也称为随机决策森林，是一种集合学习方法，是一种经典的Bagging模型，既可用于分类，也可用于回归。而集合学习算法，其实就是把多个机器学习算法综合在一起，制造出一个更加大的模型。目前应用比较广泛的集合算法就包括随机森林和梯度上升决策树。

   此外，决策树与随机森林也有相关回归模型，如DecisionTreeRegressor、RandomForestRegressor等。

''' 决策树 '''
from sklearn.tree import DecisionTreeClassifier,export_graphviz
clf = DecisionTreeClassifier(max_depth=2,···) # 决策树分类器
clf.fit(X,Y)    # 拟合
export_graphviz(clf,out_file,···) # 以DOT格式导出决策树
# criterion：gini(基尼指数)、entropy(熵)

''' 随机森林 '''
from sklearn.ensemble import RandomForestClassifier
forest = RandomForestClassifier(n_estimators,max_depth,bootstrap,···)
forest.fit(X,Y)    # 拟合
# 随机森林分类器
# n_estimators：森林中的树木数量，默认100
# bootstrap：是否在构建树时使用放回抽样，默认True

3.4 逻辑回归

   逻辑回归(Logistic Regression)是机器学习中的一种分类模型，逻辑回归是一种分类算法，其因变量是二分类；多分类的话，可以使用softmax方法进行处理。
   由于算法的简单和高效，在实际中最为常用的就是二分类，如可用来预测某件事发生是否能够发生，如预测上证指数明天是否会上涨、明天某个地区是否会下雨、某个交易是否涉嫌违规、用户是否会购买某件商品等。

$⟹\{\begin{array}{l}①线性回归模型，即y=kx+b\\ \\ ②回归结果输入到sigmoid函数，即h=g(kx+b)\end{array}$

   sigmoid函数，也称为logistic函数，即$g(z)=\frac{1}{1+e^{-z}}$；它可以将一个线性回归中的结果转化为一个[0, 1]之间的概率值，默认0.5为阈值。

''' 逻辑回归 '''
from sklearn.linear_model import LogisticRegression
logr = LogisticRegression()
# 内置函数与上述一致

四、回归算法

   线性模型是一类广泛应用于机器学习领域的预测模型，实际上线性模型并不是特指某一个模型，而是一类模型。在机器学习领域，常用的线性模型包括线性回归、岭回归、套索回归、逻辑回归和线性SVC等。

4.1 线性回归、岭回归与套索回归

   在回归分析中，线性模型的公式：$y=k_1{x}_1+k_2{x}_2+k_3{x}_3+\cdot \cdot \cdot +k_n{x}_n+b=kx+b$ 。

   线性回归，也称为普通最小二乘法(OLS)，是在回归分析中最简单也是最经典的线性模型。线性回归的原理：找到当训练数据集中y的预测值和其真实值的平方差最小的时候，所对应的k值和b值。线性回归没有可供用户调节的参数，这是它的优势，但也代表我们无法控制模型的复杂性。

   岭回归也是回归分析中常用的线性模型，它实际上是一种改良的最小二乘法。从实用的角度来说，岭回归实际上是一种能够避免过拟合的线性模型。
   在岭回归中，模型会保留所有的特征变量，但是会减小特征变量的系数值，让特征变量对预测结果的影响变小，在岭回归中是通过改变 alpha参数 来控制减小特征变量系数的程度。而这种通过保留全部特征变量，只是降低特征变量的系数值来避免过拟合的方法，我们称之为L2正则化。

   套索回归，除了岭回归之外，还有一个对线性回归进行正则化的模型，即套索回归(lasso)。和岭回归一样，套索回归也会将系数限制在非常接近0的范围内，但它进行限制的方式稍微有一点不同，我们称之为L1正则化。
   与L2正则化不同的是，L1 正则化会导致在使用套索回归的时候，有一部分特征的系数会正好等于0。也就是说，有一些特征会彻底被模型忽略掉，这也可以看成是模型对于特征进行自动选择的一种方式。把一部分系数变成0有助于让模型更容易理解，而且可以突出体现模型中最重要的那些特征。

   SGDRegressor实现了随机梯度下降学习，它支持不同的loss函数和正则化惩罚项来拟合线性回归模型。

   均方误差MSE：$MSE=\frac{{\sum }_{i=1}^m(\bar{y}-y{)}^2}{m}$， 其中 $\bar{y}是预测值，y是真实值；$

''' 线性回归 '''
from sklearn.linear_model import LinearRegression
lr = LinearRegression(fit_intercept,···) 
lr.fit(X,Y)
lr.coef_       # 返回系数-k
lr.intercept_  # 返回截距-b
lr.score(X,Y)  # 模型性能/得分
lr.predict(X_new) # 预测

''' 岭回归 : alpha默认值是1,可调节 '''
from sklearn.linear_model import Ridge
ridge = Ridge(alpha=1.5)
ridge.fit(X,Y)
ridge.coef_
ridge.intercept_
ridge.score(X,Y)
ridge.predict(X_new) # 预测

''' 套索回归 : alpha默认值是1,可调节;max_iter最大迭代次数 '''
from sklearn.linear_model import Lasso
lasso = Lasso(alpha=1.0)
lasso.fit(X,Y)
lasso.coef_
lasso.intercept_
lasso.score(X,Y)
lasso.predict(X_new) # 预测

''' SGDRegressor '''
from sklearn.linear_model import SGDRegressor
sgd = SGDRegressor(loss,fit_intercept,learning_rate,eta0)
sgd.fit(x_train,y_train)
sgd.coef_
sgd.intercept_

''' 均方误差MSE '''
from sklearn.metrics import mean_squared_error
mean_squared_error(y_true,y_pred)

• loss：默认squared_error，还可取值huber、epsilon_insensitive、squared_epsilon_insensitive；
• fit_intercept：是否计算此模型的截距，即b值；
• learning_rate：学习率，默认invscaling(eta = eta0/pow(t, power_t))，还可取值constant( eta=eta0 )、optimal( eta=1.0/(alpha*(t + t0)) )等；
• eta0：默认0.01； power_t：默认0.25； 对于一个常数值的学习率来说，可使用learning_rate=’constant’，并使用eta0来指定学习率；
  
  

4.2 欠拟合与过拟合

   机器学习中一个重要的话题便是模型的泛化能力，泛化能力强的模型才是好模型。对于训练好的模型，若在训练集表现差，在测试集表现同样会很差，这可能是欠拟合导致。欠拟合是指模型拟合程度不高，数据距离拟合曲线较远，或指模型没有很好地捕捉到数据特征，不能够很好地拟合数据。
   欠拟合的解决方法有：

• 出现的原因：学习到数据的特征过少；
• 增加数据的特征数量，可加入特征组合、高次特征等；
• 添加多项式特征，如将线性模型通过添加二次项或三次项使模型泛化能力更强；
• 减少正则化参数；或使用非线性模型，如SVM 、决策树、深度学习等模型；

   过拟合：在训练集上能够获得比其他假设更好的拟合，但在测试集上却不能很好地拟合数据，此时认为是过拟合的现象(模型过于复杂)。
   过拟合的解决办法有：

• 出现的原因：原始特征过多，存在一些嘈杂特征，模型过于复杂是因为模型尝试去兼顾各个测试数据点；
• 正则化，即在进行目标函数或代价函数优化时，在目标函数或代价函数后面加上一个正则项，一般有L1正则(岭回归)与L2正则(岭回归)等；
  
  

五、聚类算法

   上文提到过，有监督学习主要用于分类和回归，而无监督学习的一个非常重要的用途就是对数据进行聚类。聚类和分类有一定的相似之处，分类是算法基于已有标签的数据进行学习并对新数据进行分类，而聚类则是在完全没有现有标签的情况下，有算法‘猜测’哪些数据应该’堆‘在一起的，并且让算法给不同的’堆‘里的数据贴上一个数字标签。

   聚类算法，有K-means聚类、凝聚聚类以及DBSCAN这几个算法。

5.1 K-means算法

   K-means算法是一个十分经典的聚类算法，其工作原理是：假设我们的数据集中的样本因为特征不同，像小沙堆一样散布在地上，K-means算法会在小沙堆上插上旗子；而第一遍插的旗子并不能很完美地代表沙堆的分布，所以K-means还要继续，让每个旗子能够插到每个沙堆最佳的位置上，也就是数据点的均值上，这也是K-means算法名字的由来。接下来会一直重复上述的动作，直到找不出更好的位置。

from sklearn.cluster import KMeans
km = KMeans(n_clusters=8)
km.fit(X)    # 以鸢尾花为例，X是data，Y是target
km.cluster_centers_  # 各类的中心点
list(X[km.labels_==2].mean(axis=0)) # 求某一类的中心点，此处2是分类的一个值
list(X[Y==2].mean(axis=0)) # 求某一类的中心点，此处2是分类的一个值
# 使用Y还是km.labels_，具体情况具体分析吧

# n_clusters：聚类中心数量，默认8，即将数据分为n_clusters类；
# init：初始化方法，默认k-means++，还可取值random；

5.2 凝聚聚类与DBSCAN

   凝聚聚类：例子如下，观察雨后的荷叶，会发现这个现象：在重力的作用下，荷叶上的小水珠会向荷叶中心聚集，并且凝聚成一个大水珠，这可用来形象地描述凝聚聚类算法。
   实际上，凝聚聚类算法是一揽子算法的集合，而这一揽子算法的共同之处是，它们首先将每个数据点看成是一个聚类，也就是荷叶上的小水珠，然后把相似的聚类进行合并，形成了一个较大的水珠。然后重复这个过程，直到达到了停止的标准。那么停止的标准是什么呢？在scikit-learn中，停止的标准是剩下的‘大水珠’的数量。

   DBSCAN：该算法的全名称为‘基于密度的有噪声应用空间聚类’(Density-based spatial clustering of applications with noise)，其工作原理是：DBSCAN是通过对特征空间内的密度进行检测，密度大的地方它会认为是一个类，而密度相对小的地方它会认为是一个分界线。也正是由于这样的工作机制，使得DBSCAN算法不需要像K-means或凝聚聚类算法那样在一开始就指定聚类的数量。

''' 凝聚聚类:使用连线的方式进行可视化 '''
from sklearn.datasets import load_iris
from scipy.cluster.hierarchy import dendrogram, ward
import matplotlib.pyplot as plt
x = load_iris().data[:5,:2]
linkage = ward(x) # x是数组
dendrogram(linkage)
ax = plt.gca()

''' DBSCAN '''
from sklearn.cluster import DBSCAN
db = DBSCAN()
db.fit_predict(x)

六、分类的评估方法

6.1 查准率与查全率

   在分类任务下，预测结果(Predicted Condition)与正确标记(True Condition)之间存在四种不同的组合，构成混淆矩阵(适用于多分类)。

查准率/精确率：在预测结果为正例的样本中，真实结果为正例的比例；$precision=\frac{TP}{TP+FP}$

查全率/召回率：在真实结果为正例的样本中，预测结果为正例的比例；$recall=\frac{TP}{TP+FN}$

P-R曲线：以查全率为横坐标，查准率为纵坐标，就可得到P-R曲线；

''' 查准率与查全率 '''
from sklearn.metrics import precision_recall_curve
precision,recall,thresholds = precision_recall_curve(y,y_pre,pos_label=1)
print(precision,recall,thresholds)

''' 绘制P-R曲线 '''
from sklearn.metrics import PrecisionRecallDisplay
PrecisionRecallDisplay.from_predictions(y,y_pre,pos_label=1)

''' 主要分类指标的文本报告 '''
from sklearn.metrics import classification_report
report=classification_report(y,y_pre,labels=None,target_names=None)
print(report)

# y：真实值； y_pre：预测值/概率估计等；pos_label：正类的标签
# labels：指定类别对应的数字；  target_names：目标类别名称；
report结果是：每个类别精确率与召回率，f1-score反映了模型的稳健性；

6.2 ROC曲线与AUC指标

ROC曲线：以FPR为横坐标，TPR为纵坐标，就可得到ROC曲线；
AUC指标：AUC为ROC曲线的面积，其是衡量模型泛化能力的一个重要指标。若AUC大，则分类模型优；反之则分类模型差。

   $ROC曲线⟹\{\begin{array}{l}真正例率：TPR=\frac{TP}{TP+FN}\\ \\ 假正例率：FPR=\frac{FP}{TN+FP}\end{array}$

''' 返回fpr,tpr,thresholds '''
from sklearn.metrics import roc_curve
fpr,tpr,thresholds = roc_curve(y,knn.predict_proba(x)[:,1],pos_label=2)
print(fpr,tpr,thresholds)

''' 返回auc值 '''
from sklearn.metrics import roc_auc_score
auc = roc_auc_score(y,y_pre,multi_class='ovr')
print(auc)
# multi_class：取值为ovo、ovr；
# knn.predict_proba(x)：返回测试数据x的概率估计

''' 绘制ROC曲线 '''
from sklearn.metrics import RocCurveDisplay
RocCurveDisplay.from_predictions(y,y_pre,pos_label=2)

七、总结图

谢谢大家