C++：染色法判定二分图及匈牙利算法

1、二分图简介

有一种特殊的图，叫做二分图。二分图就是能以某种方式把所有点放到两个集合，放完以后，所有边都是贯穿两个集合的，没有集合内的边，一般都是无向图。画个图举个例子：

这就是一个二分图。孤立的点也是满足性质的。一个图变成二分图的方式不唯一，只要满足性质即可。再举个不是二分图的例子：

这就不是一个二分图，因为无论如何也调剂不开点1、点2和点3。

2、染色法判定二分图

那么如何判断一个图是不是二分图？有这样一条性质：
一个图是二分图的充分必要条件是图中不存在奇数环。
奇数环就是一个环中的边数为奇数。这个性质的证明这里就不做赘述，下面重点讲述如何用算法来判断二分图：染色法。

顾名思义，染色法就是把每个点依次染色，其中一条边连接的两个点一定是异色的，如果无法做到，就不是二分图了。举个例子：

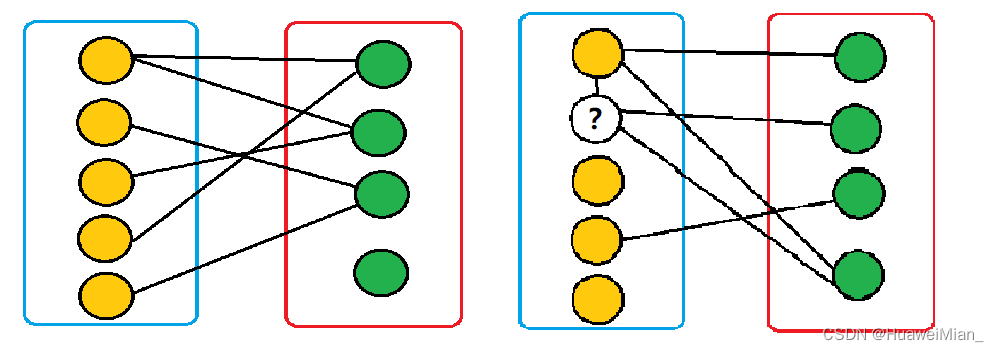
可以看到，第一个图完美的实现了染色，但是第二个图无法实现染色，所以第一个图就是二分图，而第二个图就不是二分图。用程序实现是基于搜索的，依次搜索所有点（因为有可能有不连通的点），每搜到一个未染色的点就染上颜色，搜索到相连的下一个点就染上异色，如果发现有染色矛盾（即本该染上颜色1的点却是颜色2）就立即宣布：不是二分图。使用dfs和bfs都是可以的，这里使用dfs来给出一道裸题的题解：
原题acwing 染色法判定二分图

给定一个 n 个点 m 条边的无向图，图中可能存在重边和自环。
请你判断这个图是否是二分图。
输入格式
第一行包含两个整数 n 和 m。
接下来 m 行，每行包含两个整数 u 和 v，表示点 u 和点 v 之间存在一条边。
输出格式
如果给定图是二分图，则输出 Yes，否则输出 No。
数据范围
1≤n,m≤10⁵
输入样例：

4 4
1 3
1 4
2 3
2 4

输出样例：

Yes

#include 
#include 
#include 

using namespace std;

//因为是无向图，所以边要是题目所给数量的二倍
const int N = 100010, M = 200010;

//稀疏图，用邻接表
int h[N], e[M], ne[M], idx;
//color记录每个点被染成了什么颜色
//1代表颜色1，2代表颜色2，0代表未染色
int color[N];
int n, m;

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

//u表示当前点，c表示要染成的颜色
bool dfs(int u, int c)
{
    color[u] = c;
    
    //一个简单的深度优先遍历
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];
        //如果未被染色
        if (!color[j])
        {
            if (!dfs(j, 3 - c)) return false;
        }
        //如果染色矛盾
        else if (color[j] == c) return false;
    }
    
    return true;
}

int main()
{
    cin >> n >> m;
    
    memset(h, -1, sizeof h);
    
    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b), add(b, a);
    }
    
    bool flag = true;
    //遍历所有点，防止存在不连通的点
    for (int i = 1; i <= n; i ++ )
        if (!color[i])
        {
            if (!dfs(i, 1))
            {
                flag = false;
                break;
            }
        }
        
    if (flag) puts("Yes");
    else puts("No");
    
    return 0;
}

因为要遍历一次所有的点和所有的边，所以其时间复杂度为O(m+n)。

2、匈牙利算法

匈牙利算法适用于二分图，用于求一个二分图中最大的两侧匹配数量。意思就是匹配两侧的点，点和点要通过边一一对应，求最大一一对应的点的数量。举个例子：

这样最大匹配数量就是4。那么匈牙利算法是怎样处理这类问题的呢？先把它抽象为恋爱问题，一侧为男生，一侧为女生，两者之间有边代表可以建立恋爱关系。匈牙利算法大概就是：对于每个男生，先假设所有女生都没有男朋友，找到一个可以建立关系的女生，就试试。那么就有两种情况：

1. 这个女生没有男朋友，那么就和她谈恋爱（代表成功匹配一对点）；
2. 这个女生有男朋友，那就看看他男朋友有没有其他心仪的女生，要是有并且符合条件，那就让本来的男朋友先跟另一个心仪的女生谈恋爱，自己和当前这个女生谈恋爱。如果发现本来的男朋友已经没有其他选择了，这时候只能选择放弃（匹配失败）。

这道题抽象的价值观非常抽象，大家千万不要模仿，只作为理解算法的方式即可。下面给出一道裸题以及题解：
原题acwing 二分图的最大匹配

给定一个二分图，其中左半部包含 n1 个点（编号 1∼n1），右半部包含 n2 个点（编号 1∼n2）二分图共包含 m 条边。
数据保证任意一条边的两个端点都不可能在同一部分中。
请你求出二分图的最大匹配数。
二分图的匹配：给定一个二分图 G，在 G 的一个子图 M 中，M 的边集 {E} 中的任意两条边都不依附于同一个顶点，则称 M 是一个匹配。
二分图的最大匹配：所有匹配中包含边数最多的一组匹配被称为二分图的最大匹配，其边数即为最大匹配数。
输入格式
第一行包含三个整数 n1、 n2 和 m。
接下来 m 行，每行包含两个整数 u 和 v，表示左半部点集中的点 u 和右半部点集中的点 v 之间存在一条边。
输出格式
输出一个整数，表示二分图的最大匹配数。
数据范围
1≤n1,n2≤500,
1≤u≤n1,
1≤v≤n2,
1≤m≤10⁵
输入样例：

2 2 4
1 1
1 2
2 1
2 2

输出样例：

2

#include 
#include 
#include 

using namespace std;

const int N = 510, M = 100010;

int n1, n2, m;
int h[N], e[M], ne[M], idx;
//match记录当前“女生”匹配的“男生”
int match[N];
bool st[N];

void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

bool find(int x)
{
	//遍历这个“男生”所有的“心仪女生”
    for (int i = h[x]; i != -1; i = ne[i])
    {
        int j = e[i];
        //如果当前“女生”未被考虑过
        if (!st[j])
        {
        	//记录一下当前过程此“女生”已被考虑，下次就不能再用了
        	//不然就会出现两个人不断交换“女朋友”的现象，进入死循环
        	//本质就是：在一个“男生”找女朋友的过程中，每个“女生”只能被访问一次
            st[j] = true;
            //如果当前“女生”没有男朋友 或 她的男朋友可以和别的“女生”在一起
            if (match[j] == 0 || find(match[j]))
            {
            	//那就让这个男生和当前“女生”在一起
                match[j] = x;
                //匹配成功，返回
                return true;
            }
        }
    }
    
    return false;
}

int main()
{
    cin >> n1 >> n2 >> m;
    
    memset(h, -1, sizeof h);
    
    while (m -- )
    {
        int a, b;
        scanf("%d%d", &a, &b);
        add(a, b);
    }
    
    int res = 0;
    
    //遍历所有“男生”
    for (int i = 1; i <= n1; i ++ )
    {
    	//先假设所有“女生”都没有男朋友
        memset(st, false, sizeof st);
        if (find(i)) res ++ ;
    }
    
    cout << res << endl;
    
    return 0;
}

这个算法的时间复杂度为O(mn)，因为理论上来说，每个男生都要考虑一遍所有女生，但是实际操作中不会出现这样坏的情况，所以一般时间复杂度远小于mn。

---

这两种算法的模板都比较简短且容易，但是不能忘记图论问题的难点：建图。所以不能只求掌握模板，还是要多多努力刷题，才能在遇到新的问题时游刃有余。