服务器开发设计之算法宝典

作者：lynhlzou，腾讯 IEG 后台开发工程师

孙子云：“上兵伐谋，其次伐交，其次伐兵，其下攻城”，最上乘行军打仗的方式是运用谋略，下乘的方式才是与敌人进行惨烈的厮杀。同样的，在程序设计中，解决问题的办法有很多种，陷入到与逻辑进行贴身肉搏的境况实属下下之策，而能运用优秀合理的算法才是”伐谋”的上上之策。

算法的思想精髓是值得深入研究和细细品味的，本宝典总结了服务器开发设计过程中涉及到的一些常用算法，试图尽量以简洁的文字和图表来解释和说明其中的思想原理，希望能给大家带来一些思考和启示。

思维导图

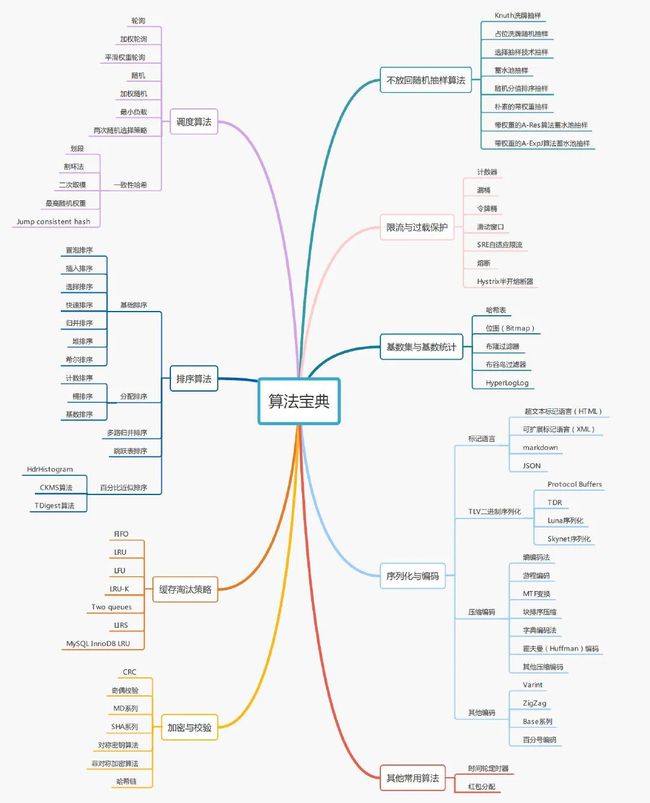
1. 调度算法

在服务器逻辑开发设计中，调度算法随处可见，资源的调度，请求的分配，负载均衡的策略等等都与调度算法相关。调度算法没有好坏之分，最适合业务场景的才是最好的。

1.1. 轮询

轮询是非常简单且常用的一种调度算法，轮询即将请求依次分配到各个服务节点，从第一个节点开始，依次将请求分配到最后一个节点，而后重新开始下一轮循环。最终所有的请求会均摊分配在每个节点上，假设每个请求的消耗是一样的，那么轮询调度是最平衡的调度（负载均衡）算法。

1.2. 加权轮询

有些时候服务节点的性能配置各不相同，处理能力不一样，针对这种的情况，可以根据节点处理能力的强弱配置不同的的权重值，采用加权轮询的方式进行调度。

加权轮询可以描述为：

1. 调度节点记录所有服务节点的当前权重值，初始化为配置对应值。

2. 当有请求需要调度时，每次分配选择当前权重最高的节点，同时被选择的节点权重值减一。

3. 若所有节点权重值都为零，则重置为初始化时配置的权重值。

最终所有请求会按照各节点的权重值成比例的分配到服务节点上。假设有三个服务节点{a,b,c}，它们的权重配置分别为{2,3,4}，那么请求的分配次序将是{c,b,c,a,b,c,a,b,c}，如下所示：

请求序号	当前权重	选中节点	调整后权重
1	{2,3,4}	c	{2,3,3}
2	{2,3,3}	b	{2,2,3}
3	{2,2,3}	c	{2,2,2}
4	{2,2,2}	a	{1,2,2}
5	{1,2,2}	b	{1,1,2}
6	{1,1,2}	c	{1,1,1}
7	{1,1,1}	a	{0,1,1}
8	{0,1,1}	b	{0,0,1}
9	{0,0,1}	c	{0,0,0}

1.3. 平滑权重轮询

加权轮询算法比较容易造成某个服务节点短时间内被集中调用，导致瞬时压力过大，权重高的节点会先被选中直至达到权重次数才会选择下一个节点，请求连续的分配在同一个节点上的情况，例如假设三个服务节点{a,b,c}，权重配置分别是{5,1,1}，那么加权轮询调度请求的分配次序将是{a,a,a,a,a,b,c}，很明显节点 a 有连续的多个请求被分配。

为了应对这种问题，平滑权重轮询实现了基于权重的平滑轮询算法。所谓平滑，就是在一段时间内，不仅服务节点被选择次数的分布和它们的权重一致，而且调度算法还能比较均匀的选择节点，不会在一段时间之内集中只选择某一个权重较高的服务节点。

平滑权重轮询算法可以描述为：

1. 调度节点记录所有服务节点的当前权重值，初始化为配置对应值。

2. 当有请求需要调度时，每次会先把各节点的当前权重值加上自己的配置权重值，然后选择分配当前权重值最高的节点，同时被选择的节点权重值减去所有节点的原始权重值总和。

3. 若所有节点权重值都为零，则重置为初始化时配置的权重值。

同样假设三个服务节点{a,b,c}，权重分别是{5,1,1}，那么平滑权重轮询每一轮的分配过程如下表所示：

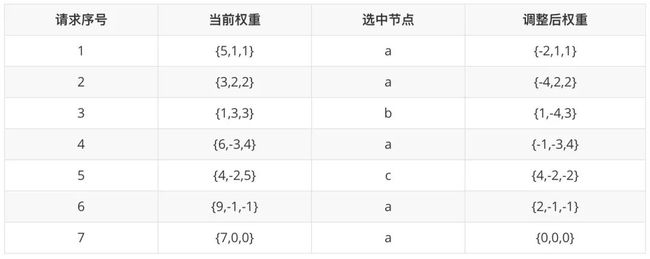最终请求分配的次序将是{ a, a, b, a, c, a, a}，相对于普通权重轮询算法会更平滑一些。

1.4. 随机

随机即每次将请求随机地分配到服务节点上，随机的优点是完全无状态的调度，调度节点不需要记录过往请求分配情况的数据。理论上请求量足够大的情况下，随机算法会趋近于完全平衡的负载均衡调度算法。

1.5. 加权随机

类似于加权轮询，加权随机支持根据服务节点处理能力的大小配置不同的的权重值，当有请求需要调度时，每次根据节点的权重值做一次加权随机分配，服务节点权重越大，随机到的概率就越大。最终所有请求分配到各服务节点的数量与节点配置的权重值成正比关系。

1.6. 最小负载

实际应用中，各个请求很有可能是异构的，不同的请求对服务器的消耗各不相同，无论是使用轮询还是随机的方式，都可能无法准确的做到完全的负载均衡。最小负载算法是根据各服务节点当前的真实负载能力进行请求分配的，当前负载最小的节点会被优先选择。

最小负载算法可以描述为：

1. 服务节点定时向调度节点上报各自的负载情况，调度节点更新并记录所有服务节点的当前负载值。

2. 当有请求需要调度时，每次分配选择当前负载最小（负载盈余最大）的服务节点。

负载情况可以统计节点正在处理的请求量，服务器的 CPU 及内存使用率，过往请求的响应延迟情况等数据，综合这些数据以合理的计算公式进行负载打分。

1.7. 两次随机选择策略

最小负载算法可以在请求异构情况下做到更好的均衡性。然而一般情况下服务节点的负载数据都是定时同步到调度节点，存在一定的滞后性，而使用滞后的负载数据进行调度会导致产生“群居”行为，在这种行为中，请求将批量地发送到当前某个低负载的节点，而当下一次同步更新负载数据时，该节点又有可能处于较高位置，然后不会被分配任何请求。再下一次又变成低负载节点被分配了更多的请求，一直处于这种很忙和很闲的循环状态，不利于服务器的稳定。

为应对这种情况，两次随机选择策略算法做了一些改进，该算法可以描述为：

1. 服务节点定时向调度节点上报各自的负载情况，调度节点更新并记录所有服务节点的当前负载值。

2. 从所有可用节点列表中做两次随机选择操作，得到两个节点。

3. 比较这两个节点负载情况，选择负载更低的节点作为被调度的节点。

两次随机选择策略结合了随机和最小负载这两种算法的优点，使用负载信息来选择节点的同时，避免了可能的“群居”行为。

1.8. 一致性哈希

为了保序和充分利用缓存，我们通常希望相同请求 key 的请求总是会被分配到同一个服务节点上，以保持请求的一致性，既有了一致性哈希的调度方式。

关于一致性哈希算法，笔者曾在 km 发表过专门的文章《一致性哈希方案在分布式系统中应用对比》，详细介绍和对比了它们的优缺点以及对比数据，有兴趣的同学可以前往阅读。

1.8.1. 划段

最简单的一致性哈希方案就是划段，即事先规划好资源段，根据请求的 key 值映射找到所属段，比如通过配置的方式，配置 id 为[1-10000]的请求映射到服务节点 1，配置 id 为[10001-20000]的请求映射到节点 2 等等，但这种方式存在很大的应用局限性，对于平衡性和稳定性也都不太理想，实际业务应用中基本不会采用。

1.8.2. 割环法

割环法的实现有很多种，原理都类似。割环法将 N 台服务节点地址哈希成 N 组整型值，该组整型即为该服务节点的所有虚拟节点，将所有虚拟节点打散在一个环上。

请求分配过程中，对于给定的对象 key 也哈希映射成整型值，在环上搜索大于该值的第一个虚拟节点，虚拟节点对应的实际节点即为该对象需要映射到的服务节点。

如下图所示，对象 K1 映射到了节点 2，对象 K2 映射到节点 3。

割环法实现复杂度略高，时间复杂度为 O(log(vn)),（其中，n 是服务节点个数，v 是每个节点拥有的虚拟节点数），它具有很好的单调性，而平衡性和稳定性主要取决于虚拟节点的个数和虚拟节点生成规则，例如 ketama hash 割环法采用的是通过服务节点 ip 和端口组成的字符串的 MD5 值，来生成 160 组虚拟节点。

1.8.3. 二次取模

取模哈希映射是一种简单的一致性哈希方式，但是简单的一次性取模哈希单调性很差，对于故障容灾非常不好，一旦某台服务节点不可用，会导致大部分的请求被重新分配到新的节点，造成缓存的大面积迁移，因此有了二次取模的一致性哈希方式。

二次取模算法即调度节点维护两张服务节点表：松散表（所有节点表）和紧实表（可用节点表）。请求分配过程中，先对松散表取模运算，若结果节点可用，则直接选取；若结果节点已不可用，再对紧实表做第二次取模运算，得到最终节点。如下图示：

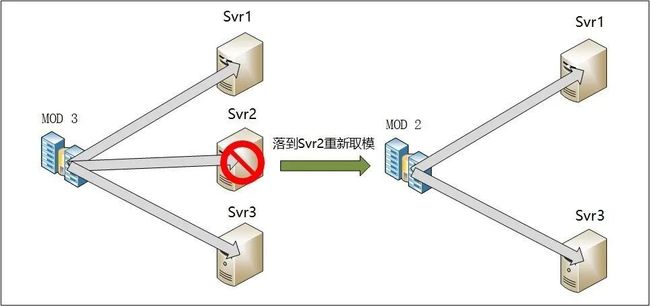
二次取模算法实现简单，时间复杂度为 O(1)，具有较好的单调性，能很好的处理缩容和节点故障的情况。平衡性和稳定性也比较好，主要取决于对象 key 的分布是否足够散列（若不够散列，也可以加一层散列函数将 key 打散）。

1.8.4. 最高随机权重

最高随机权重算法是以请求 key 和节点标识为参数进行一轮散列运算（如 MurmurHash 算法），得出所有节点的权重值进行对比，最终取最大权重值对应的节点为目标映射节点。可以描述为如下公式：

散列运算也可以认为是一种保持一致性的伪随机的方式，类似于前面讲到的普通随机的调度方式，通过随机比较每个对象的随机值进行选择。

这种方式需要 O(n)的时间复杂度，但换来的是非常好的单调性和平衡性，在节点数量变化时，只有当对象的最大权重值落在变化的节点上时才受影响，也就是说只会影响变化的节点上的对象的重新映射，因此无论扩容，缩容和节点故障都能以最小的代价转移对象，在节点数较少而对于单调性要求非常高的场景可以采用这种方式。

1.8.5. Jump consistent hash

jump consistent hash 通过一种非常简单的跳跃算法对给定的对象 key 算出该对象被映射的服务节点，算法如下：

int JumpConsistentHash(unsigned long long key, int num_buckets)
{
    long long  b = -1, j = 0;
    while (j < num_buckets) {
        b = j;
        key = key * 2862933555777941757ULL + 1;
        j = (b + 1) * (double(1LL << 31) / double((key >> 33) + 1));
    }
    return b;
}

这个算法乍看难以理解，它其实是下面这个算法的一个变种，只是将随机函数通过线性同余的方式改造而来的。

int ch(int key, int num_buckets) {
    random.seed(key) ;
    int b = -1; //  bucket number before the previous jump
    int j = 0; // bucket number before the current jump
    while(j < num_buckets){
        b = j;
        double r = random.next(); //  0

它也是一种伪随机的方式，通过随机保证了平衡性，而这里随机函数用到的种子是各个请求的 key 值，因此保证了一致性。它与最高随机权重的差别是这里的随机不需要对所有节点都进行一次随机，而是通过随机值跳跃了部分节点的比较。

jump consistent hash 实现简单，零内存消耗，时间复杂度为 O(log(n))。具有很高的平衡性，在单调性方面，扩容和缩容表现较好，但对于中间节点故障，理想情况下需要将故障节点与最后一个节点调换，需要将故障节点和最后的节点共两个节点的对象进行转移。###1.8.6. 小结

一致性哈希方式还有很多种类，通常结合不同的散列函实现。也有些或为了更简单的使用，或为了更好的单调性，或为了更好的平衡性等而对以上这些方式进行的改造等，如二次 Jump consistent hash 等方式。另外也有结合最小负载方式等的变种，如有限负载一致性哈希会根据当前负载情况对所有节点限制一个最大负载，在一致性哈希中对 hash 进行映射时跳过已达到最大负载限制的节点，实际应用过程中可根据业务情况自行做更好的调整和结合。

2. 不放回随机抽样算法

不放回随机抽样即从 n 个数据中抽取 m 个不重复的数据。关于不放回随机抽样算法，笔者曾在 km 发表过专门的文章详细演绎和实现了各种随机抽样算法的原理和过程，以及它们的优缺点和适用范围，有兴趣的同学可以前往阅读。

2.1. Knuth 洗牌抽样

不放回随机抽样可以当成是一次洗牌算法的过程，利用洗牌算法来对序列进行随机排列，然后选取前 m 个序列作为抽样结果。

Knuth 洗牌算法是在 Fisher-Yates 洗牌算法中改进而来的，通过位置交换的方式代替了删除操作，将每个被删除的数字交换为最后一个未删除的数字（或最前一个未删除的数字）。

Knuth 洗牌算法可以描述为：

• 生成数字 1 到 n 的随机排列（数组索引从 1 开始）

• for i from 1 to n-1 do

  j ← 随机一个整数值 i ≤ j < n

  交换 a[j] 和 a[i]

运用 Knuth 洗牌算法进行的随机抽样的方式称为 Knuth 洗牌随机抽样算法，由于随机抽样只需要抽取 m 个序列，因此洗牌流程只需洗到前 m 个数据即可。

2.2. 占位洗牌随机抽样

Knuth 洗牌算法是一种 in-place 的洗牌，即在原有的数组直接洗牌，尽管保留了原数组的所有元素，但它还是破坏了元素之间的前后顺序，有些时候我们希望原数组仅是可读的（如全局配置表），不会因为一次抽样遭到破坏，以满足可以对同一原始数组多次抽样的需求，如若使用 Knuth 抽样算法，必须对原数组先做一次拷贝操作，但这显然不是最好的做法，更好的办法在 Knuth 洗牌算法的基础上，不对原数组进行交换操作，而是通过一个额外的 map 来记录元素间的交换关系，我们称为占位洗牌算法。

占位洗牌算法过程演示如下：

最终，洗牌的结果为 3，5，2，4，1。

运用占位洗牌算法实现的随机抽样的方式称为占位洗牌随机抽样，同样的，我们依然可以只抽取到前 m 个数据即可。这种算法对原数组不做任何修改，代价是增加不大于 的临时空间。

2.3. 选择抽样技术抽样

洗牌算法是对一个已经预初始化好的数据列表进行洗牌，需要在内存中全量缓存数据列表，如果数据总量 n 很大，并且单条记录的数据也很大，那么在内存中缓存所有数据记录的做法会显得非常的笨拙。而选择选择抽样技术算法，它不需要预先全量缓存数据列表，从而可以支持流式处理。

选择抽样技术算法可以描述为：

1. 生成 1 到 n 之间的随机数 U

2. 如果 U≥m，则跳转到步骤 4

3. 把这个记录选为样本，m 减 1，n 减 1。如果 m>0，则跳转到步骤 1，否则取样完成，算法终止

4. 跳过这个记录，不选为样本，n 减 1，跳转到步骤 1

选择抽样技术算法过程演示如下：

最终，抽样的结果为 2，5。

可以证明，选择选择抽样技术算法对于每个数被选取的概率都是 。

选择抽样技术算法虽然不需要将数据流全量缓存到内存中，但他仍然需要预先准确的知道数据量的总大小即 n 值。它的优点是能保持输出顺序与输入顺序不变，且单个元素是否被抽中可以提前知道。

2.4. 蓄水池抽样

很多时候我们仍然不知道数据总量 n，上述的选择抽样技术算法就需要扫描数据两次，第一次先统计 n 值，第二次再进行抽样，这在流处理场景中仍然有很大的局限性。

Alan G. Waterman 给出了一种叫蓄水池抽样（Reservoir Sampling）的算法，可以在无需提前知道数据总量 n 的情况下仍然支持流处理场景。

蓄水池抽样算法可以描述为：

1. 数据游标 i←0，将 i≤m 的数据一次放入蓄水池，并置 pool[i] ←i

2. 生成 1 到 i 之间的随机数 j

3. 如果 j>m，则跳转到步骤 5

4. 把这个记录选为样本，删除原先蓄水池中 pool[j]数据，并置 pool[j] ←i

5. 游标 i 自增 1，若 i

蓄水池抽样算法过程演示如下：

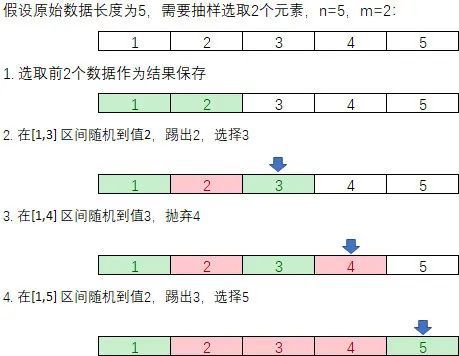
最终，抽样的结果为 1，5。

可以证明，每个数据被选中且留在蓄水池中的概率为 。

2.5. 随机分值排序抽样

洗牌算法也可以认为就是将数据按随机的方式做一个排序，从 n 个元素集合中随机抽取 m 个元素的问题就相当于是随机排序之后取前 m 排名的元素，基于这个原理，我们可以设计一种通过随机分值排序的方式来解决随机抽样问题。

随机分值排序算法可以描述为：

1. 系统维护一张容量为 m 的排行榜单

2. 对于每个元素都给他们随机一个（0,1] 区间的分值，并根据随机分值插入排行榜

3. 所有数据处理完成，最终排名前 m 的元素即为抽样结果

尽管随机分值排序抽样算法相比于蓄水池抽样算法并没有什么好处，反而需要增加额外的排序消耗，但接下来的带权重随机抽样将利用到它的算法思想。

2.6. 朴素的带权重抽样

很多需求场景数据元素都需要带有权重，每个元素被抽取的概率是由元素本身的权重决定的，诸如全服消费抽奖类活动，需要以玩家在一定时间段内的总消费额度为权重进行抽奖，消费越高，最后中奖的机会就越大，这就涉及到了带权重的抽样算法。

朴素的带权重随机算法也称为轮盘赌选择法，将数据放置在一个假想的轮盘上，元素个体的权重越高，在轮盘上占据的空间就越多，因此就更有可能被选中。

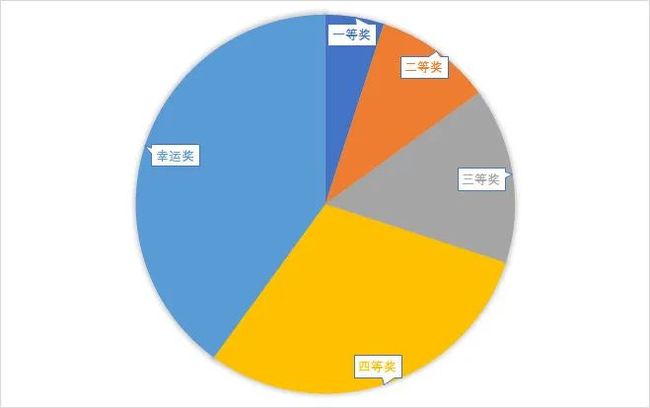
假设上面轮盘一到四等奖和幸运奖的权重值分别为 5,10,15,30,40，所有元素权重之和为 100，我们可以从[1, 100] 中随机得到一个值，假设为 45，而后从第一个元素开始，不断累加它们的权重，直到有一个元素的累加权重包含 45，则选取该元素。如下所示：

由于权重 45 处于四等奖的累加权重值当中，因此最后抽样结果为四等奖。

若要不放回的选取 m 个元素，则需要先选取一个，并将该元素从集合中踢除，再反复按同样的方法抽取其余元素。

这种抽样算法的复杂度是 ，并且将元素从集合中删除破坏了原数据的可读属性，更重要的是这个算法需要多次遍历数据，不适合在流处理的场景中应用。

2.7. 带权重的 A-Res 算法蓄水池抽样

朴素的带权重抽样算法需要内存足够容纳所有数据，破坏了原数据的可读属性，时间复杂度高等缺点，而经典的蓄水池算法高效的实现了流处理场景的大数据不放回随机抽样，但对于带权重的情况，就不能适用了。

A-Res（Algorithm A With a Reservoir） 是蓄水池抽样算法的带权重版本，算法主体思想与经典蓄水池算法一样都是维护含有 m 个元素的结果集，对每个新元素尝试去替换结果集中的元素。同时它巧妙的利用了随机分值排序算法抽样的思想，在对数据做随机分值的时候结合数据的权重大小生成排名分数，以满足分值与权重之间的正相关性，而这个 A-Res 算法生成随机分值的公式就是：

其中 为第 i 个数据的权重值， 是从（0,1]之间的一个随机值。

A-Res 算法可以描述为：

1. 对于前 m 个数, 计算特值 ，直接放入蓄水池中

2. 对于从 m+1,m+2,...,n 的第 i 个数，通过公式 计算特征值 ，如若特征值超过蓄水池中最小值，则替换最小值

该算法的时间复杂度为 ，且可以完美的运用在流式处理场景中。

2.8. 带权重的 A-ExpJ 算法蓄水池抽样

A-Res 需要对每个元素产生一个随机数，而生成高质量的随机数有可能会有较大的性能开销，《Weighted random sampling with a reservoir》论文中给出了一种更为优化的指数跳跃的算法 A-ExpJ 抽样（Algorithm A with exponential jumps），它能将随机数的生成量从 减少到 ，原理类似于通过一次额外的随机来跳过一段元素的特征值 的计算。

A-ExpJ 算法蓄水池抽样可以描述为：

1. 对于前 m 个数， 计算特征值 ，其中 为第 i 个数据的权重值， 是从（0,1]之间的一个随机值，直接放入蓄水池中

2. 对于从 m+1,m+2,...,n 的第 i 个数，执行以下步骤

3. 计算阈值 ， ，其中 r 为（0,1]之间的一个随机值， 为蓄水池中的最小特征值

4. 跳过部分元素并累加这些元素权重值 ，直到第 i 个元素满足

5. 计算当前元素特征值 ，其中 为(,1]之间的一个随机值，, 为蓄水池中的最小特征值， 为当前元素权重值

6. 使用当前元素替换蓄水池中最小特征值的元素

7. 更新阈值 ，

有点不好理解，show you the code:

function aexpj_weight_sampling(data_array, weight_array, n, m)
    local result, rank = {}, {}
    for i=1, m do
        local rand_score = math.random() ^ (1 / weight_array[i])
        local idx = binary_search(rank, rand_score)
        table.insert(rank, idx, {score = rand_score, data = data_array[i]})
    end

    local weight_sum, xw = 0, math.log(math.random()) / math.log(rank[m].score)
    for i=m+1, n do
        weight_sum = weight_sum + weight_array[i]
        if weight_sum >= xw then
            local tw = rank[m].score ^ weight_array[i]
            local rand_score = (math.random()*(1-tw) + tw) ^ (1 / weight_array[i])
            local idx = binary_search(rank, rand_score)
            table.insert(rank, idx, {score = rand_score, data = data_array[i]})
            table.remove(rank)
            weight_sum = 0
            xw = math.log(math.random()) / math.log(rank[m].score)
        end
    end

    for i=1, m do
        result[i] = rank[i].data
    end

    return result
end

3. 排序算法

3.1. 基础排序

基础排序是建立在对元素排序码进行比较的基础上进行的排序算法。

3.1.1. 冒泡排序

冒泡排序是一种简单直观的排序算法。它每轮对每一对相邻元素进行比较，如果相邻元素顺序不符合规则，则交换他们的顺序，每轮将有一个最小（大）的元素浮上来。当所有轮结束之后，就是一个有序的序列。

过程演示如下：

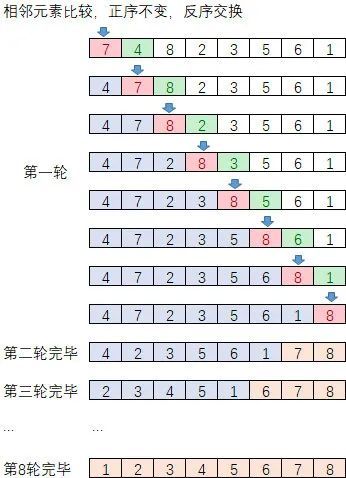
3.1.2. 插入排序

插入排序通过构建有序序列，初始将第一个元素看做是一个有序序列，后面所有元素看作未排序序列，从头到尾依次扫描未排序序列，对于未排序数据，在已排序序列中从后向前扫描，找到相应位置并插入。

过程演示如下：

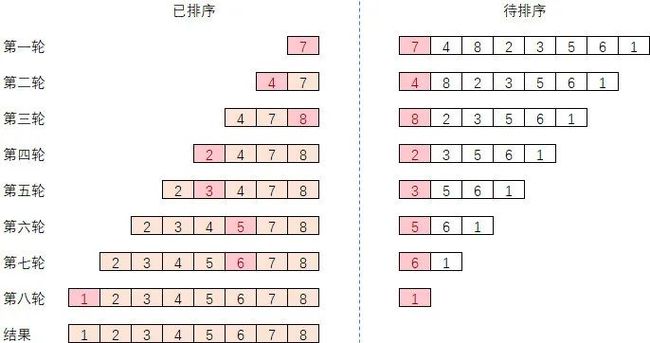
3.1.3. 选择排序

选择排序首先在未排序序列中找到最小（大）元素，存放到已排序序列的起始位置。再从剩余未排序元素中继续寻找最小（大）元素，然后放到已排序序列的末尾。直到所有元素处理完毕。

过程演示如下：

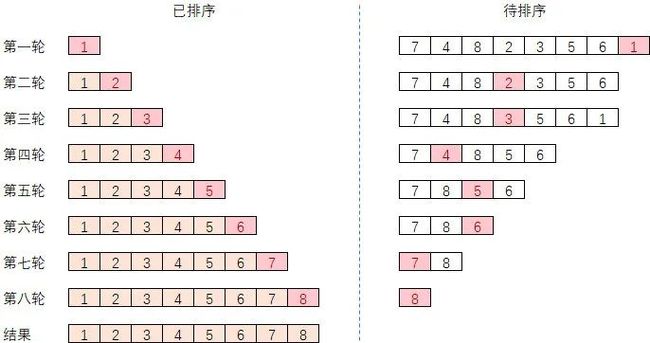
插入排序是每轮会处理好第一个未排序序列的位置，而选择排序是每轮固定好一个已排序序列的位置。冒泡排序也是每轮固定好一个已排序序列位置，它与选择排序之间的不同是选择排序直接选一个最小（大）的元素出来，而冒泡排序通过依次相邻交换的方式选择出最小（大）元素。

3.1.4. 快速排序

快速排序使用分治法策略来把一串序列分为两个子串序列。快速排序是一种分而治之的思想在排序算法上的典型应用。本质上来看，快速排序应该算是在冒泡排序基础上的递归分治法。

快速排序从数列中挑出一个元素，称为"基准"，所有元素比基准值小的摆放在基准前面，比基准值大的摆在基准的后面。一轮之后该基准就处于数列的中间位置。并递归地把小于基准值元素的子数列和大于基准值元素的子数列进行排序。

过程演示如下：

3.1.5. 归并排序

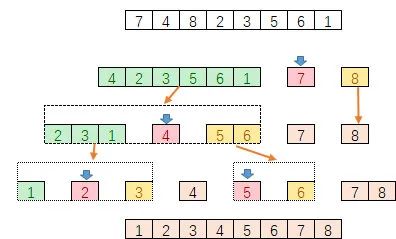
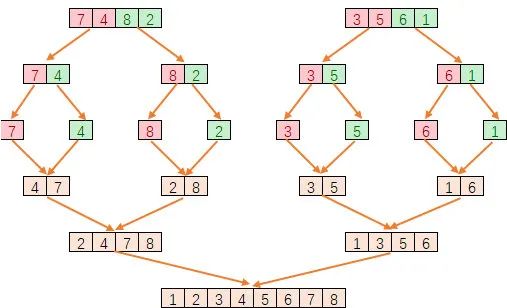
归并排序是建立在归并操作上的一种有效的排序算法，也是采用分治法的一个非常典型的应用。归并排序首先将序列二分成最小单元，而后通过归并的方式将两两已经有序的序列合并成一个有序序列，直到最后合并为一个最终有序序列。

过程演示如下：

3.1.6. 堆排序

堆排序（Heapsort）是利用堆这种数据结构所设计的一种排序算法。堆是一个近似完全二叉树的结构，并同时满足堆的性质：子结点的键值或索引总是小于（或者大于）它的父节点。

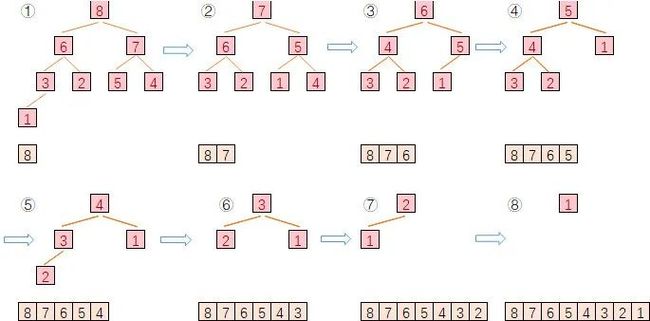
堆排序首先创建一个堆，每轮将堆顶元素弹出，而后进行堆调整，保持堆的特性。所有被弹出的元素序列即是最终排序序列。

过程演示如下：

3.1.7. 希尔排序

希尔排序，也称递减增量排序算法，是插入排序的一种更高效的改进版本，但希尔排序是非稳定排序算法。

插入排序在对几乎已经排好序的数据操作时，效率高，即可以达到线性排序的效率。但插入排序一般来说是低效的，因为插入排序每次只能将数据移动一位。

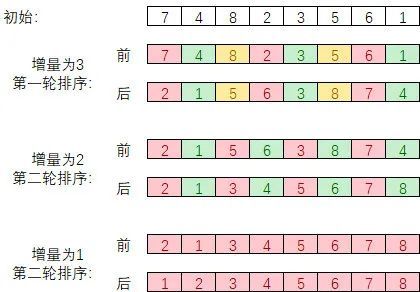
希尔排序通过将比较的全部元素分为几个区域来提升插入排序的性能。这样可以让一个元素可以一次性地朝最终位置前进一大步。然后算法再取越来越小的步长进行排序，算法的最后一步就是普通的插入排序，但是到了这步，需排序的数据几乎是已排好的了（此时插入排序较快）。

过程演示如下：

3.2. 分配排序

基础排序是建立在对元素排序码进行比较的基础上，而分配排序是采用“分配”与“收集”的办法。

3.2.1. 计数排序

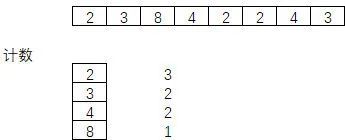
计数排序的核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。作为一种线性时间复杂度的排序，计数排序要求输入的数据必须是有确定范围的整数。

计数排序的特征：当输入的元素是 n 个 0 到 k 之间的整数时，它的运行时间是 。计数排序不是比较排序，排序的速度快于任何比较排序算法。

由于用来计数的数组的长度取决于待排序数组中数据的范围（等于待排序数组的最大值与最小值的差加上 1），这使得计数排序对于数据范围很大的数组，需要大量时间和空间。

过程演示如下：

3.2.2. 桶排序

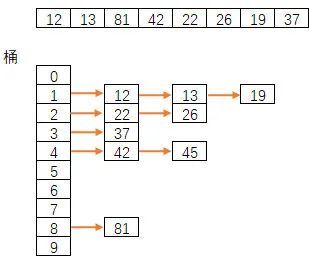
桶排序是计数排序的升级版，它利用了函数的映射关系，桶排序高效与否的关键就在于这个映射函数的确定。比如我们可以将排序数据进行除 10 运算，运算结果中具有相同的商值放入相同的桶中，即每十个数会放入相同的桶中。

过程演示如下：

为了使桶排序更加高效，我们需要做到这两点：

1. 在额外空间充足的情况下，尽量增大桶的数量

2. 使用的映射函数能够将输入的所有数据均匀的分配到所有桶中

计数排序本质上是一种特殊的桶排序，当桶的个数取最大值(max-min+1)的时候，桶排序就变成了计数排序。

3.2.3. 基数排序

基数排序的原理是将整数按位数切割成不同的数字，然后对每个位数分别比较。基数排序首先按最低有效位数字进行排序，将相同值放入同一个桶中，并按最低位值顺序叠放，然后再按次低有效位排序，重复这个过程直到所有位都进行了排序，最终即是一个有序序列。

过程演示如下：

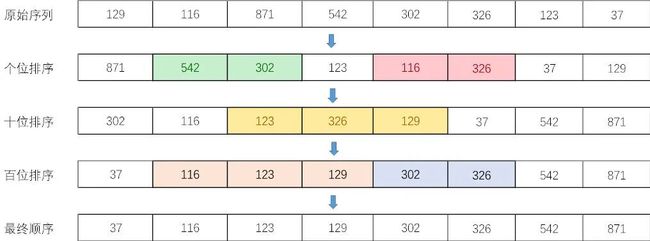
基数排序也是一种桶排序。桶排序是按值区间划分桶，基数排序是按数位来划分，基数排序可以看做是多轮桶排序，每个数位上都进行一轮桶排序。

3.3. 多路归并排序

多路归并排序算法是将多个已经有序的列表进行归并排序，合成为一组有序的列表的排序过程。

k 路归并排序可以描述为：

1. 初始时取出 k 路有序列表中首个元素放入比较池。

2. 从比较池中取最小（大）的元素加入到结果列表，同时将该元素所在有序列表的下一个元素放入比较池（若有）。

3. 重新复进行步骤 2，直到所有队列的所有元素都已取出。

每次在比较池中取最小（大）的元素时，需要进行一次 k 个数据的比较操作，当 k 值较大时，会严重影响多路归并的效率，为提高效率，可以使用“败者树”来实现这样的比较过程。

败者树是完全二叉树，败者树相对的是胜者树，胜者树每个非终端结点（除叶子结点之外的其它结点）中的值都表示的是左右孩子相比较后的胜者。

如下图所示是一棵胜者树：

而败者树双亲结点表示的是左右孩子比较之后的失败者，但在上一层的比较过程中，仍然是拿前一次的胜者去比较。

如下图所示是一颗败者树：

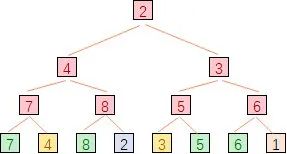
叶子节点的值是：{7,4,8,2,3,5,6,1}，7 与 4 比较，7 是败者，4 是胜者，因此他们的双亲节点是 7，同样 8 与 2 比较，8 是败者，表示在他们双亲节点上，而 7 与 8 的双亲节点需要用他们的胜者去比较，即用 4 与 2 比较，4 是败者，因此 7 与 8 的双亲节点记录的是 4，依此类推。

假设 k=8，败者树归并排序的过程演示如下所示：

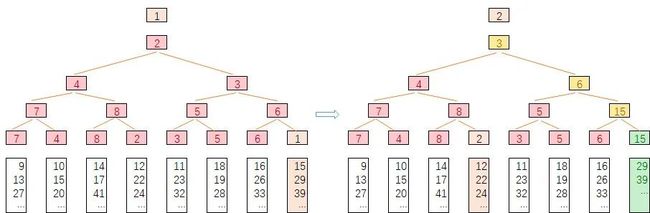
首先构建起败者数，最后的胜者是 1，第二次将 1 弹出，取 1 所在的第 8 列的第二个数 15 放入 1 所在的叶子节点位置，并进行败者树调整，此时只需调整原 1 所在分支的祖先节点，最后胜者为 2，后续过程依此类推。最后每轮的最终胜者序列即是最后的归并有序序列。

胜者树和败者树的本质是利用空间换时间的做法，通过辅助节点记录两两节点的比较结果来达到新插入节点后的比较和调整性能。

笔者曾经基于 lua 语言利用败者树实现多路归并排序算法，有兴趣可以前往阅读。

3.4. 跳跃表排序

跳跃表（Skip Lists）是一种有序的数据结构，它通过在每个节点中随机的建立上层辅助查找节点，从而达到快速访问节点的目的（与败者树的多路归并排序有异曲同工之妙）。

跳跃列表按层建造，底层是一个普通的有序链表，包含所有元素。每个更高层都充当下面列表的“快速通道”，第 i 层中的元素按某个固定的概率 p（通常为 1/2 或 1/4）随机出现在第 i+1 层中。每个元素平均出现在 1/(1-p)个列表中，而最高层的元素在 个列表中出现。

如下是四层跳跃表结构的示意：

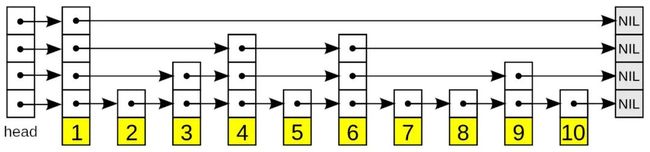
在查找目标元素时，从顶层列表、头元素起步，沿着每层链表搜索，直至找到一个大于或等于目标的元素，或者到达当前层列表末尾。如果该元素等于目标元素，则表明该元素已被找到；如果该元素大于目标元素或已到达链表末尾，则退回到当前层的上一个元素，然后转入下一层进行搜索。依次类推，最终找到该元素或在最底层底仍未找到（不存在）。

当 p 值越大，快速通道就越稀疏，占用空间越小，但查找速度越慢，反之，则占用空间大查找速度快，通过选择不同 p 值，就可以在查找代价和存储代价之间获取平衡。

由于跳跃表使用的是链表，加上增加了近似于以二分方式的辅助节点，因此查询，插入和删除的性能都很理想。在大部分情况下，跳跃表的效率可以和平衡树相媲美，它是一种随机化的平衡方案，在实现上比平衡树要更为简单，因而得到了广泛的应用，如 redis 的 zset，leveldb，我司的 apollo 排行榜等都使用了跳跃表排序方案。

3.5. 百分比近似排序

在流处理场景中，针对大容量的排序榜单，全量存储和排序需要消耗的空间及时间都很高，不太现实。实际应用中，对于长尾数据的排序，一般也只需要显示百分比近似排名，通过牺牲一定的精确度来换取高性能和高实时性。

3.5.1. HdrHistogram 算法

HdrHistogram 使用的是直方图统计算法，直方图算法类似于桶排序，原理就是创建一个直方图，以一定的区间间隔记录每个区间上的数据总量，预测排名时只需统计当前值所在区间及之前区间的所有数量之和与总数据量之间的比率。

区间分割方式可以采用线性分割和指数分割方式：

1. 线性分割，数据以固定长度进行分割，假设数据范围是[1-1000000]，以每 100 的间隔划分为 1 个区间，总共需要划分 10000 个区间桶。

2. 指数分割，基于指数倍的间隔长度进行分割，假设数据范围是[1-1000000]，以 2 的幂次方的区间[, ]进行划分，总共只需要划分 20 个区间桶。

HdrHistogram 为了兼顾内存和估算的准确度，同时采用了线性分割和指数分割的方式，相当于两层的直方图算法，第一层使用指数分割方式，可以粗略的估算数据的排名范围位置，第二层使用线性分割方式，更加精确的估算出数据的排名位置。线性区间划分越小结果越精确，但需要的内存越多，可以根据业务精确度需求控制线性区间的大小。

直方图算法需要预先知道数据的最大值，超过最大值的数据将存不进来。HdrHistogram 提供了一个自动扩容的功能，以解决数据超过预估值的问题，但是这个自动扩容方式存在一个很高的拷贝成本。

3.5.2. CKMS 算法

HdrHistogram 是一种静态分桶的算法，当数据序列是均匀分布的情况下，有比较好的预测效果，然而实际应用中数据有可能并不均匀，很有可能集中在某几个区间上，CKMS 采用的是动态分桶的方式，在数据处理过程中不断调整桶的区间间隔和数量。

CKMS 同时引入一个可配置的错误率的概念，在抉择是否开辟新桶时，根据用户设置的错误率进行计算判定。判定公式为：区间间隔=错误率* 数据总量。

下图是一个桶合并的例子：

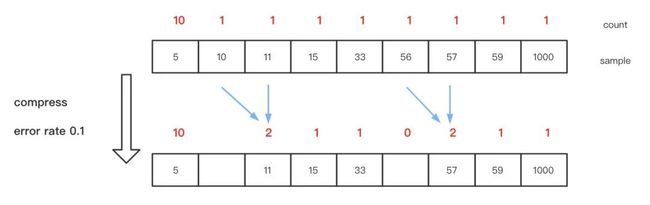
如上所示，假设错误率设置为 0.1，当数据总量大于 10 个时，通过判定公式计算出区间间隔为 1，因此将会对区间间隔小于等于 1 的相邻桶进行合并。

CKMS 算法不需要预知数据的范围，用户可以根据数据的性质设置合适的错误率，以控制桶的空间占用和精确度之间的平衡关系。

3.5.3. TDigest 算法

Tdigest 算法的思想是近似算法常用的素描法（Sketch），用一部分数据来刻画整体数据集的特征，就像我们日常的素描画一样，虽然和实物有差距，但是却看着和实物很像，能够展现实物的特征。它本质上也是一种动态分桶的方式。

TDigest 算法估计具体的百分位数时，都是根据百分位数对应的两个质心去线性插值计算的，和精准百分位数的计算方式一样。首先我们根据百分位 q 和所有质心的总权重计算出索引值；其次找出和对应索引相邻的两个质心；最终可以根据两个质心的均值和权重用插值的方法计算出对应的百分位数。（实际的计算方法就是加权平均）。

由此我们可以知道，百分位数 q 的计算误差要越小，其对应的两个质心的均值应该越接近。TDigest 算法的关键就是如何控制质心的数量，质心的数量越多，显然估计的精度就会越高，但是需要的内存就会越多，计算效率也越低；但是质心数量越少，估计的精度就很低，所以就需要一个权衡。

一种 TDigest 构建算法 buffer-and-merge 可以描述为：

1. 将新加入的数据点加入临时数组中，当临时数组满了或者需要计算分位数时，将临时数组中的数据点和已经存在的质心一起排序。（其中数据点和质心的表达方式是完全一样的：平均值和权重，每个数据点的平均值就是其本身，权重默认是 1）。

2. 遍历所有的数据点和质心，满足合并条件的数据点和质心就进行合并，如果超出权重上限，则创建新的质心数，否则修改当前质心数的平均值和权重。

假设我们有 200 个质心，那么我们就可以将 0 到 1 拆分 200 等份，则每个质心就对应 0.5 个百分位。假如现在有 10000 个数据点，即总权重是 10000，我们按照大小对 10000 个点排序后，就可以确定每个质心的权重（相当于质心代表的数据点的个数）应该在 10000/200 = 500 左右，所以说当每个质心的权重小于 500 时，我们就可以将当前数据点加入当前的质心，否则就新建一个质心。

实际应用中，我们可能更加关心 90%，95%，99%等极端的百分位数，所以 TDigest 算法特意优化了 q=0 和 q=1 附近的百分位精度，通过专门的映射函数 K 保证了 q=0 和 q=1 附近的质心权重较小，数量较多。

另外一种 TDigest 构建算法是 AVL 树的聚类算法，与 buffer-and-merge 算法相比，它通过使用 AVL 二叉平衡树的方式来搜索数据点最靠近的质心数，找到最靠近的质心数后，将二者进行合并。

4. 限流与过载保护

复杂的业务场景中，经常容易遇到瞬时请求量的突增，很有可能会导致服务器占用过多资源，发生了大量的重试和资源竞争，导致响应速度降低、超时、乃至宕机，甚至引发雪崩造成整个系统不可用的情况。

为应对这种情况，通常需要系统具备可靠的限流和过载保护的能力，对于超出系统承载能力的部分的请求作出快速拒绝、丢弃处理，以保证本服务或下游服务系统的稳定。

4.1. 计数器

计数器算法是限流算法里最简单也是最容易实现的一种算法。计数器算法可以针对某个用户的请求，或某类接口请求，或全局总请求量进行限制。

比如我们设定针对单个玩家的登录协议，每 3 秒才能请求一次，服务器可以在玩家数据上记录玩家上一次的登录时间，通过与本次登录时间进行对比，判断是否已经超过了 3 秒钟来决定本次请求是否需要继续处理。

又如针对某类协议，假设我们设定服务器同一秒内总登录协议请求次数不超过 100 条，我们可以设置一个计数器，每当一个登录请求过来的时候，计数器加 1，如果计数器值大于 100 且当前请求与第一个请求间隔时间还在 1 秒内，那么就判定为达到请求上限，拒绝服务，如果该请求与第一个请求间隔已经超过 1 秒钟，则重置计数器的值为 0，并重新计数。

计数器算法存在瞬时流量的临界问题，即在时间窗口切换时，前一个窗口和后一个窗口的请求量都集中在时间窗口切换的前后，在最坏的情况下，可能会产生两倍于阈值流量的请求。

为此也可以使用多个不同间隔的计数器相结合的方式进行限频，如可以限制登录请求 1 秒内不超过 100 的同时 1 分钟内不超过 1000 次。

4.2. 漏桶

漏桶算法原理很简单，假设有一个水桶，所有水（请求）都会先丢进漏桶中，漏桶则以固定的速率出水（处理请求），当请求量速率过大，水桶中的水则会溢出（请求被丢弃）。漏桶算法能保证系统整体按固定的速率处理请求。

如下图所示：

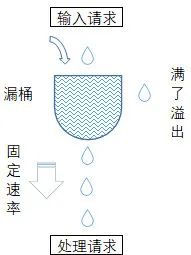
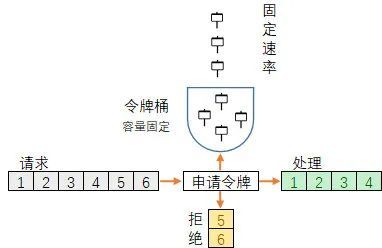
4.3. 令牌桶

对于很多应用场景来说，除了要求能够限制请求的固定处理速率外，还要求允许某种程度的突发请求量，这时候漏桶算法可能就不合适了。

令牌桶算法的原理是系统会以一个恒定的速度往桶里放入令牌，而如果请求需要被处理，则需要先从桶里获取一个令牌，当桶里没有令牌可取时，则拒绝服务。

令牌桶算法大概描述如下：

1. 所有的请求在处理之前都需要拿到一个可用的令牌才会被处理。

2. 根据限流大小，设置按照一定的速率往桶里添加令牌。

3. 桶设置最大的放置令牌限制，当桶满时、新添加的令牌就被丢弃。

4. 请求达到后首先要获取令牌桶中的令牌，拿着令牌才可以进行其他的业务逻辑，处理完业务逻辑之后，将令牌直接删除。

如下图所示：

4.4. 滑动窗口

计数器，漏桶和令牌桶算法是在上游节点做的限流，通过配置系统参数做限制，不依赖于下游服务的反馈数据，对于异构的请求不太适用，且需要预估下游节点的处理能力。

滑动窗口限频类似于 TCP 的滑动窗口协议，设置一个窗口大小，这个大小即当前最大在处理中的请求量，同时记录滑动窗口的左右端点，每次发送一个请求时滑动窗口右端点往前移一格，每次收到请求处理完毕响应后窗口左端点往前移一格，当右端点与左端点的差值超过最大窗口大小时，等待发送或拒绝服务。

如下图所示：

4.5. SRE 自适应限流

滑动窗口是以固定的窗口大小限制请求，而 Google 的 SRE 自适应限流相当于是一个动态的窗口，它根据过往请求的成功率动态调整向后端发送请求的速率，当成功率越高请求被拒绝的概率就越小；反之，当成功率越低请求被拒绝的概率就相应越大。

SRE 自适应限流算法需要在应用层记录过去两分钟内的两个数据信息：

1. requests：请求总量，应用层尝试的请求数

2. accepts：成功被后端处理的请求数

请求被拒绝的概率 p 的计算公式如下：

1. 其中 K 为倍率因子，由用户设置（比如 2），从算法公式可以看出：

2. 在正常情况下 requests 等于 accepts，新请求被决绝的概率 p 为 0，即所有请求正常通过

3. 当后端出现异常情况时，accepts 的数量会逐渐小于 requests，应用层可以继续发送请求直到 requests 等于 ，一旦超过这个值，自适应限流启动，新请求就会以概率 p 被拒绝。

4. 当后端逐渐恢复时，accepts 逐渐增加，概率 p 会增大，更多请求会被放过，当 accepts 恢复到使得 大于等于 requests 时，概率 p 等于 0，限流结束。

我们可以针对不同场景中处理更多请求带来的风险成本与拒绝更多请求带来的服务损失成本之间进行权衡，调整 K 值大小：

• 降低 K 值会使自适应限流算法更加激进（拒绝更多请求，服务损失成本升高，风险成本降低）。

• 增加 K 值会使自适应限流算法不再那么激进（放过更多请求，服务损失成本降低，风险成本升高）。

如对于某些处理该请求的成本与拒绝该请求的成本的接近场景，系统高负荷运转造成很多请求处理超时，实际已无意义，然而却还是一样会消耗系统资源的情况下，可以调小 K 值。

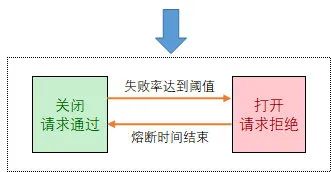
4.6. 熔断

熔断算法原理是系统统计并定时检查过往请求的失败（超时）比率，当失败（超时）率达到一定阈值之后，熔断器开启，并休眠一段时间，当休眠期结束后，熔断器关闭，重新往后端节点发送请求，并重新统计失败率。如此周而复始。

如下图所示：

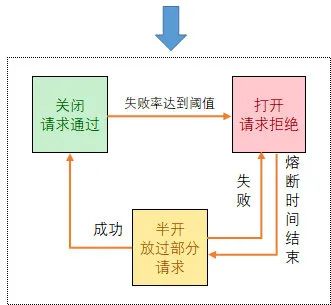
4.7. Hystrix 半开熔断器

Hystrix 中的半开熔断器相对于简单熔断增加了一种半开状态，Hystrix 在运行过程中会向每个请求对应的节点报告成功、失败、超时和拒绝的状态，熔断器维护计算统计的数据，根据这些统计的信息来确定熔断器是否打开。如果打开，后续的请求都会被截断。然后会隔一段时间，尝试半开状态，即放入一部分请求过去，相当于对服务进行一次健康检查，如果服务恢复，熔断器关闭，随后完全恢复调用，如果失败，则重新打开熔断器，继续进入熔断等待状态。

如下图所示：

5. 序列化与编码

数据结构序列化是指将数据结构或对象状态转换成可取用格式（例如存成文件，存于缓冲，或经由网络传输），以留待后续在相同或另一台计算机环境中，能恢复原先状态的过程。经过依照序列化格式重新获取字节的结果时，可以利用它来产生与原始对象相同语义的副本。

5.1. 标记语言

标记语言是一种将文本（Text）以及文本相关的其他信息结合起来，展现出关于文档结构和数据处理细节的计算机文字编码。

5.1.1. 超文本标记语言（HTML）

HTML 是一种用于创建网页的标准标记语言。HTML 是一种基础技术，常与 CSS、JavaScript 一起被众多网站用于设计网页、网页应用程序以及移动应用程序的用户界面。网页浏览器可以读取 HTML 文件，并将其渲染成可视化网页。HTML 描述了一个网站的结构语义随着线索的呈现，使之成为一种标记语言而非编程语言。

5.1.2. 可扩展标记语言（XML）

XML 是一种标记语言，设计用来传送及携带数据信息。每个 XML 文档都由 XML 声明开始，在前面的代码中的第一行就是 XML 声明。这一行代码会告诉解析器或浏览器这个文件应该按照 XML 规则进行解析。

XML 文档的字符分为标记（Markup）与内容（content）两类。标记通常以<开头，以>结尾；或者以字符&开头，以;结尾。不是标记的字符就是内容。一个 tag 属于标记结构，以<开头，以>结尾。

元素是文档逻辑组成，或者在 start-tag 与匹配的 end-tag 之间，或者仅作为一个 empty-element tag。

属性是一种标记结构，在 start-tag 或 empty-element tag 内部的“名字-值对”。例如：每个元素中，一个属性最多出现一次，一个属性只能有一个值。

5.1.3. Markdown

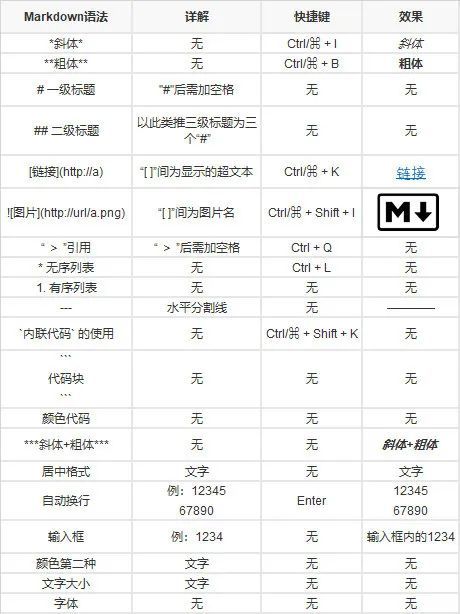
Markdown 是一种轻量级标记语言，创始人为约翰·格鲁伯。它允许人们使用易读易写的纯文本格式编写文档，然后转换成有效的 XHTML（或者 HTML）文档。这种语言吸收了很多在电子邮件中已有的纯文本标记的特性。

由于 Markdown 的轻量化、易读易写特性，并且对于图片，图表、数学式都有支持，目前许多网站都广泛使用 Markdown 来撰写帮助文档或是用于论坛上发表消息。如 GitHub、Reddit、Diaspora、Stack Exchange、OpenStreetMap 、SourceForge、简书等，甚至还能被用来撰写电子书。当然还有咱们的 KM 平台，很强大。

Markdown 语法格式如下：

5.1.4. JSON

JSON 是以数据线性化为目标的轻量级标记语言，相比于 XML，JSON 更加简洁、轻量和具有更好的可读性。

JSON 的基本数据类型和编码规则：

• 数值：十进制数，不能有前导 0，可以为负数，可以有小数部分。还可以用 e 或者 E 表示指数部分。不能包含非数，如 NaN。不区分整数与浮点数。

• 字符串：以双引号""括起来的零个或多个 Unicode 码位。支持反斜杠开始的转义字符序列。

• 布尔值：表示为 true 或者 false。

• 数组：有序的零个或者多个值。每个值可以为任意类型。序列表使用方括号[，]括起来。元素之间用逗号,分割。形如：[value, value]

• 对象：若干无序的“键-值对”（key-value pairs），其中键只能是字符串。建议但不强制要求对象中的键是独一无二的。对象以花括号{开始，并以}结束。键-值对之间使用逗号分隔。键与值之间用冒号:分割。

• 空值：值写为 null

5.2. TLV 二进制序列化

很多高效得数据序列化方式都是采用类 TLV（Tag+Length+Value）的方式对数据进行序列化和反序列化，每块数据以 Tag 开始，Tag 即数据标签，标识接下来的数据类型是什么，Length 即长度，标识接下来的数据总长，Value 即数据的实际内容，结合 Tag 和 Length 的大小即可获取当前这块数据内容。

5.2.1. Protocol Buffers

Protocol Buffers（简称：ProtoBuf）是一种开源跨平台的序列化数据结构的协议，它是一种灵活，高效，自动化的结构数据序列化方法，相比 XML 和 JSON 更小、更快、更为简单。

Protocol Buffers 包含一个接口描述语言.proto 文件，描述需要定义的一些数据结构，通过程序工具根据这些描述产生.cc 和.h 文件代码，这些代码将用来生成或解析代表这些数据结构的字节流。

Protocol Buffers 编码后的消息都是 Key-Value 形式，Key 的值由 field_number（字段标号）和 wire_type（编码类型）组合而成，规则为：key = field_number << 3 | wire type。

field_number 部分指示了当前是哪个数据成员，通过它将 cc 和 h 文件中的数据成员与当前的 key-value 对应起来。

wire type 为字段编码类型，有以下几类：

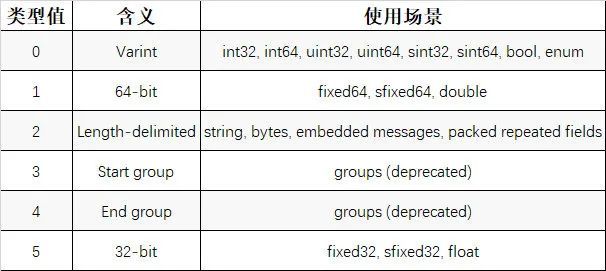
Protocol Buffers 编码特征：

• 整型数据采用 varint 编码（见 5.4.1 节），以节省序列化后数据大小。

• 对于有符号整型，先进行 zigzag 编码（见 5.4.2 节）调整再进行 varint 数据编码，以减小负整数序列化后数据大小。

• string、嵌套结构以及 packed repeated fields 的编码类型是 Length-delimited，它们的编码方式统一为 tag+length+value。

5.2.2. TDR

TDR 是腾讯互娱研发部自研跨平台多语言数据表示组件，主要用于数据的序列化反序列化以及数据的存储。TDR 通过 XML 文件来定义接口和结构的描述，通过程序工具根据这些描述产生.tdr 和.h 文件代码，用于序列化和反序列化这些数据结构。

TDR1.0 的版本是通过版本剪裁方式来序列化反序列化，需要事先维护好字段版本号，序列化反序列化时通过剪裁版本号来完成兼容的方式，只支持单向的高版本兼容低版本数据。

TDR2.0 整体上与 Protocol Buffers 相似，TDR2.0 支持消息协议的前后双向兼容，整型数据同样支持 varint 编码和 zigzag 调整的方式，在对 TLV 中 Length 部分进行处理时，采用定长编解码方式，以浪费序列化空间的代价来获取更高性能，避免了类似 Protocol Buffers 中不必要的内存拷贝（或者是预先计算大小）的过程。

Protocol Buffers 和 TDR 都有接口描述语言，这使得它们的序列化更高效，数据序列化后也更加紧凑。

5.2.3. Luna 序列化

luna 库是开源的基于 C++17 的 lua/C++绑定库，它同时也实现了针对 lua 数据结构的序列化和反序列化功能，用于 lua 结构数据的传输和存储。

Lua 语言中需要传输和存储的数据类型主要有：nil，boolean，number，string，table。因此在序列化过程中，luna 将类型定义为以下九种类型。

序列化方式如下：

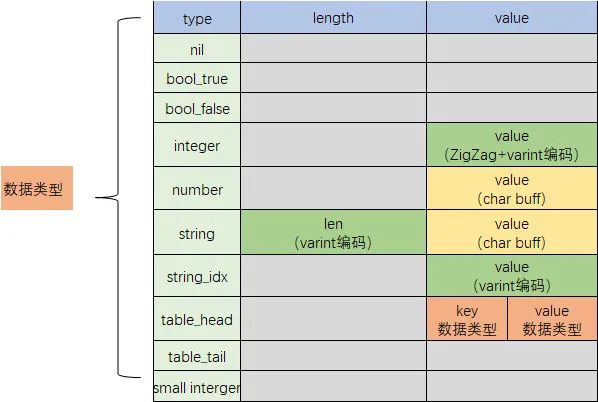
整体上也是类似于 Protocol Buffers 和 TDR 的 TLV 编码方式，同时针对 lua 类型结构的特性做了一些效率上的优化。

主要特性如下：

• Boolean 类型区分为 bool_true 和 bool_false，只需在增加 2 种 type 值就可以解决。

• 整型 integer 同样采用 varint 压缩编码方式，无需额外字节记录长度。

• 有符号整型，同样是先进行 zigzag 调整再进行 varint 数据编码。

• 字符串类型分为 string 和 string_idx，编码过程中会缓存已经出现过的字符串，对于后续重复出现的字符串记录为 string_idx 类型，value 值记录该字符串第一次出现的序号，节约字符串占用的空间。

• 对于小于 246（255 减去类型数量 9）的小正整型数，直接当成不同类型处理，加上数值 9 之后记录在 type 中，节约空间。

• Table 为嵌套结构，用 table_head 和 table_tail 两种类型表示开始和结束。key 和 value 分别进行嵌套编码。

5.2.4. Skynet 序列化

Skynet 是一个应用广泛的为在线游戏服务器打造的轻量级框架。但实际上它也不仅仅使用在游戏服务器领域。skynet 的核心是由 C 语言编写，但大多数 skynet 服务使用 lua 编写，因此它也实现了针对 lua 数据结构的序列化和反序列化功能。

序列化方式如下：

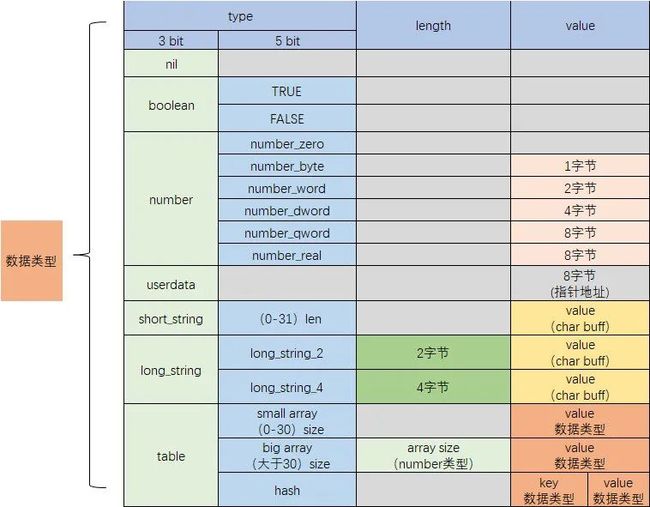
主要特性如下：

• Type 类型通过低 3 位和高 5 位来区分主类型和子类型。

• Boolean 单独主类型，子类型字段用 1 和 0 区分 true 和 false。

• 整型使用 number 主类型，子类型分为 number_zero（0 值），number_byte（小于 8 位的正整数），number_word（小于 16 位的正整数），number_dword（小于 32 位的正负整数），number_qword（其他整数），number_real（浮点数）。

• 字符串类型分为短字符串 short_string 和长字符串 long_string，小于 32 字节长度的字符串记录为 short_string 主类型，低 5 位的子类型记录长度。long_string 又分为 2 字节（长度小于 0x1000）和 4 字节（长度大于等于 0x1000）长字符串，分别用 2 字节 length 和 4 字节 length 记录长度。

• Table 类型会区分 array 部分和 hash 部分，先将 array 部分序列化，array 部分又分为小 array 和大 array，小 array（0-30 个元素）直接用 type 的低 5 位的子类型记录大小，大 array 的子类型固定为 31，大小通过 number 类型编码。Hash 部分需要将 key 和 value 分别进行嵌套编码。

• Table 的结束没有像 luna 一样加了专门的 table_tail 标识，而是通过 nil 类型标识。

5.3. 压缩编码

压缩算法从对数据的完整性角度分有损压缩和无损压缩。

有损压缩算法通过移除在保真前提下需要的必要数据之外的其小细节，从而使文件变小。在有损压缩里，因部分有效数据的移除，恢复原文件是不可能的。有损压缩主要用来存储图像和音频文件，通过移除数据达到比较高的压缩率。

无损压缩，也能使文件变小，但对应的解压缩功能可以精确的恢复原文件，不丢失任何数据。无损数据压缩被广泛的应用于计算机领域，数据的传输和存储系统中均使用无损压缩算法。

接下来我们主要是介绍几种无损压缩编码算法。

5.3.1. 熵编码法

一种主要类型的熵编码方式是对输入的每一个符号，创建并分配一个唯一的前缀码，然后，通过将每个固定长度的输入符号替换成相应的可变长度前缀无关（prefix-free）输出码字替换，从而达到压缩数据的目的。每个码字的长度近似与概率的负对数成比例。因此，最常见的符号使用最短的码。

霍夫曼编码和算术编码是两种最常见的熵编码技术。如果预先已知数据流的近似熵特性（尤其是对于信号压缩），可以使用简单的静态码。

5.3.2. 游程编码

又称行程长度编码或变动长度编码法，是一种与资料性质无关的无损数据压缩技术，基于“使用变动长度的码来取代连续重复出现的原始资料”来实现压缩。举例来说，一组资料串"AAAABBBCCDEEEE"，由 4 个 A、3 个 B、2 个 C、1 个 D、4 个 E 组成，经过变动长度编码法可将资料压缩为 4A3B2C1D4E（由 14 个单位转成 10 个单位）。

5.3.3. MTF 变换

MTF（Move-To-Front）是一种数据编码方式，作为一个额外的步骤，用于提高数据压缩技术效果。MTF 主要使用的是数据“空间局部性”，也就是最近出现过的字符很可能在接下来的文本附近再次出现。

过程可以描述为：

1. 首先维护一个文本字符集大小的栈表，“recently used symbols”（最近访问过的字符），其中每个不同的字符在其中占一个位置，位置从 0 开始编号。

2. 扫描需要重新编码的文本数据，对于每个扫描到的字符，使用该字符在“recently used symbols”中的 index 替换，并将该字符提到“recently used symbols”的栈顶的位置（index 为 0 的位置）。重复上一步骤，直到文本扫描结束。

5.3.4. 块排序压缩

当一个字符串用该算法转换时，算法只改变这个字符串中字符的顺序而并不改变其字符。如果原字符串有几个出现多次的子串，那么转换过的字符串上就会有一些连续重复的字符，这对压缩是很有用的。

块排序变换（Burrows-Wheeler Transform）算法能使得基于处理字符串中连续重复字符的技术（如 MTF 变换和游程编码）的编码更容易被压缩。

块排序变换算法将输入字符串的所有循环字符串按照字典序排序，并以排序后字符串形成的矩阵的最后一列为其输出。

5.3.5. 字典编码法

由 Abraham Lempel 和 Jacob Ziv 独创性的使用字典编码器的 LZ77/78 算法及其 LZ 系列变种应用广泛。

LZ77 算法通过使用编码器或者解码器中已经出现过的相应匹配数据信息替换当前数据从而实现压缩功能。这个匹配信息使用称为长度-距离对的一对数据进行编码，它等同于“每个给定长度个字符都等于后面特定距离字符位置上的未压缩数据流。”编码器和解码器都必须保存一定数量的缓存数据。保存这些数据的结构叫作滑动窗口，因为这样所以 LZ77 有时也称作滑动窗口压缩。编码器需要保存这个数据查找匹配数据，解码器保存这个数据解析编码器所指代的匹配数据。

LZ77 算法针对过去的数据进行处理，而 LZ78 算法却是针对后来的数据进行处理。LZ78 通过对输入缓存数据进行预先扫描与它维护的字典中的数据进行匹配来实现这个功能，在找到字典中不能匹配的数据之前它扫描进所有的数据，这时它将输出数据在字典中的位置、匹配的长度以及找不到匹配的数据，并且将结果数据添加到字典中。

5.3.6. 霍夫曼（Huffman）编码

霍夫曼编码把文件中一定位长的值看作是符号，比如把 8 位长的 256 种值，也就是字节的 256 种值看作是符号。根据这些符号在文件中出现的频率，对这些符号重新编码。对于出现次数非常多的，用较少的位来表示，对于出现次数非常少的，用较多的位来表示。这样一来，文件的一些部分位数变少了，一些部分位数变多了，由于变小的部分比变大的部分多，所以整个文件的大小还是会减小，所以文件得到了压缩。

要进行霍夫曼编码，首先要把整个文件读一遍，在读的过程中，统计每个符号（我们把字节的 256 种值看作是 256 种符号）的出现次数。然后根据符号的出现次数，建立霍夫曼树，通过霍夫曼树得到每个符号的新的编码。对于文件中出现次数较多的符号，它的霍夫曼编码的位数比较少。对于文件中出现次数较少的符号，它的霍夫曼编码的位数比较多。然后把文件中的每个字节替换成他们新的编码。

5.3.7. 其他压缩编码

• deflate 是同时使用了 LZ77 算法与霍夫曼编码的一个无损数据压缩算法。

• gzip 压缩算法的基础是 deflate。

• bzip2 使用 Burrows-Wheeler transform 将重复出现的字符序列转换成同样字母的字符串，然后用 move-to-front 变换进行处理，最后使用霍夫曼编码进行压缩。

• LZ4 着重于压缩和解压缩速度，它属于面向字节的 LZ77 压缩方案家族。

• Snappy（以前称 Zippy）是 Google 基于 LZ77 的思路用 C++语言编写的快速数据压缩与解压程序库，并在 2011 年开源，它的目标并非最大压缩率或与其他压缩程序库的兼容性，而是非常高的速度和合理的压缩率。

转自网络的压缩率和性能对比：

Format	Size Before(byte)	Size After(byte)	Compress Expend(ms)	UnCompress Expend(ms)	MAX CPU(%)
bzip2	35984	8677	11591	2362	29.5
gzip	35984	8804	2179	389	26.5
deflate	35984	9704	680	344	20.5
lzo	35984	13069	581	230	22
lz4	35984	16355	327	147	12.6
snappy	35984	13602	424	88	11

5.4. 其他编码

5.4.1. Varint

前文所提到的 Varint 整型压缩编码方式，它使用一个或多个字节序列化整数的方法，把整数编码为变长字节。

Varint 编码将每个字节的低 7bit 位用于表示数据，最高 bit 位表示后面是否还有字节，其中 1 表示还有后续字节，0 表示当前是最后一个字节。当整型数值很小时，只需要极少数的字节进行编码，如数值 9，它的编码就是 00001001，只需一个字节。

如上图所示，假设要编码的数据 123456，二进制为：11110001001000000，按 7bit 划分后，每 7bit 添加高 1 位的是否有后续字节标识，编码为 110000001100010000000111，占用 3 个字节。

对于 32 位整型数据经过 Varint 编码后需要 1~5 个字节，小的数字使用 1 个字节，大的数字使用 5 个字节。64 位整型数据编码后占用 1~10 个字节。在实际场景中小数字的使用率远远多于大数字，因此通过 Varint 编码对于大部分场景都可以起到很好的压缩效果。

5.4.2. ZigZag

zigzag 编码的出现是为了解决 varint 对负数编码效率低的问题。对于有符号整型，如果数值为负数，二进制就会非常大，例如-1 的 16 进制：0xffff ffff ffff ffff，对应的二进制位全部是 1，使用 varint 编码需要 10 个字节，非常不划算。

zigzag 编码的原理是将有符号整数映射为无符号整数，使得负数的二进制数值也能用较少的 bit 位表示。它通过移位来实现映射。

由于补码的符号位在最高位，对于负数，符号位为 1，这导致 varint 压缩编码无法压缩，需要最大变长字节来存储，因此首先将数据位整体循环左移 1 位，最低位空出留给符号位使用，另外，对于实际使用中，绝对值小的负数应用场景比绝对值大的负数应用场景大的多，但绝对值小的负数的前导 1 更多（如-1，全是 1），因此对于负整数，再把数据位按取反规则操作，将前导 1 置换为 0，以达到可以通过 varint 编码能有效压缩的目的。

最终经过 zigzag 编码后绝对值小的正负整数都能编码为绝对值相对小的正整数，编码效果如下：

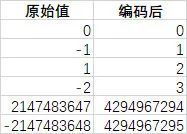
5.4.3. Base 系列

有的字符在一些环境中是不能显示或使用的，比如&, =等字符在 URL 被保留为特殊作用的字符，比如一些二进制码如果转成对应的字符的话，会有很多不可见字符和控制符（如换行、回车之类），这时就需要对数据进行编码。Base 系列的就是用来将字节编码为 ASCII 中的可见字符的，以便能进行网络传输和打印等。

Base 系列编码的原理是将字节流按固定步长切片，然后通过映射表为每个切片找一个对应的、可见的 ASCII 字符，最终重组为新的可见字符流。

Base16 也称 hex，它使用 16 个可见字符来表示二进制字符串，1 个字符使用 2 个可见字符来表示，因此编码后数据大小将翻倍。

Base32 使用 32 个可见字符来表示二进制字符串，5 个字符使用 8 个可见字符表示，最后如果不足 8 个字符，将用“=”来补充，编码后数据大小变成原来的 8/5。

Base64 使用 64 个可见字符来表示二进制字符串， 3 个字符使用 4 个可见字符来表示，编码后数据大小变成原来的 4/3。

Base64 索引表如下：

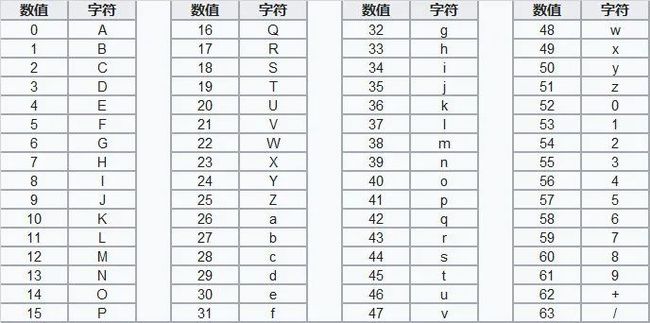
笔者曾经用 lua 实现过Base64 算法，有兴趣可以前往阅读。

5.4.4. 百分号编码

百分号编码又称 URL 编码（URL encoding），是特定上下文的统一资源定位符（URL）的编码机制，实际上也适用于统一资源标志符（URI）的编码。

百分号编码同样也是为了使 URL 具有可传输性，可显示性以及应对二进制数据的完整性而进行的一种编码规则。

百分号编码规则为把字符的 ASCII 的值表示为两个 16 进制的数字，然后在其前面放置转义字符百分号“%”。

URI 所允许的字符分作保留与未保留。保留字符是那些具有特殊含义的字符，例如：斜线字符用于 URL（或 URI）不同部分的分界符；未保留字符没有这些特殊含义。

以下是 RFC3986 中对保留字符和未保留字符的定义：

百分号编码可描述为：

• 未保留字符不需要编码

• 如果一个保留字符需要出现在 URI 一个路径成分的内部, 则需要进行百分号编码

• 除了保留字符和未保留字符（包括百分号字符本身）的其它字符必须用百分号编码

• 二进制数据表示为 8 位组的序列，然后对每个 8 位组进行百分号编码

6. 加密与校验

6.1. CRC

CRC 循环冗余校验（Cyclic redundancy check）是一种根据网络数据包或电脑文件等数据产生简短固定位数校验码的一种散列函数，主要用来检测或校验数据传输或者保存后可能出现的错误。生成的数字在传输或者存储之前计算出来并且附加到数据后面，然后接收方进行检验确定数据是否发生变化。它是一类重要的线性分组码，编码和解码方法简单，检错和纠错能力强，在通信领域广泛地用于实现差错控制。

CRC 是两个字节数据流采用二进制除法（没有进位，使用 XOR 来代替减法）相除所得到的余数。其中被除数是需要计算校验和的信息数据流的二进制表示；除数是一个长度为（n+1）的预定义（短）的二进制数，通常用多项式的系数来表示。在做除法之前，要在信息数据之后先加上 n 个 0。CRC 是基于有限域 GF（2）（即除以 2 的同余）的多项式环。简单的来说，就是所有系数都为 0 或 1（又叫做二进制）的多项式系数的集合，并且集合对于所有的代数操作都是封闭的。

6.2. 奇偶校验

奇偶校验(Parity Check)是一种校验代码传输正确性的方法。根据被传输的一组二进制代码的数位中“1”的个数是奇数或偶数来进行校验。采用奇数的称为奇校验，反之，称为偶校验。通常专门设置一个奇偶校验位，用它使这组代码中“1”的个数为奇数或偶数。若用奇校验，则当接收端收到这组代码时，校验“1”的个数是否为奇数，从而确定传输代码的正确性。

以偶校验位来说，如果一组给定数据位中 1 的个数是奇数，补一个 bit 为 1，使得总的 1 的个数是偶数。例：0000001, 补一个 bit 为 1 即 00000011。

以奇校验位来说，如果给定一组数据位中 1 的个数是奇数，补一个 bit 为 0，使得总的 1 的个数是奇数。例：0000001, 补一个 bit 为 0 即 00000010。

偶校验实际上是循环冗余校验的一个特例，通过多项式 x + 1 得到 1 位 CRC。

6.3. MD 系列

MD 系列算法（Message-Digest Algorithm）用于生成信息摘要特征码，具有不可逆性和高度的离散性，可以看成是一种特殊的散列函数（见 8.1 节），一般认为可以唯一地代表原信息的特征，通常用于密码的加密存储，数字签名，文件完整性验证等。

MD4 是麻省理工学院教授 Ronald Rivest 于 1990 年设计的一种信息摘要算法，它是一种用来测试信息完整性的密码散列函数的实现，其摘要长度为 128 位。它是基于 32 位操作数的位操作来实现的。这个算法影响了后来的算法如 MD5、SHA 家族和 RIPEMD 等

MD5 消息摘要算法是一种被广泛使用的密码散列函数，可以产生出一个 128 位（16 个字符）的散列值，用于确保信息传输完整一致。MD5 由美国密码学家罗纳德·李维斯特（Ronald Linn Rivest）设计，于 1992 年公开，用以取代 MD4 算法。MD5 是输入不定长度信息，输出固定长度 128-bits 的算法。经过程序流程，生成四个 32 位数据，最后联合起来成为一个 128-bits 散列。基本方式为，求余、取余、调整长度、与链接变量进行循环运算，得出结果。

MD6 消息摘要算法使用默克尔树形式的结构，允许对很长的输入并行进行大量散列计算。该算法的 Block size 为 512 bytes(MD5 的 Block Size 是 512 bits), Chaining value 长度为 1024 bits, 算法增加了并行 机制，适合于多核 CPU。相较于 MD5，其安全性大大改进，加密结构更为完善，但其有证明的版本速度太慢，而效率高的版本并不能给出类似的证明。

6.4. SHA 系列

SHA（Secure Hash Algorithm）是一个密码散列函数家族，是 FIPS 所认证的安全散列算法。

SHA1 是由 NISTNSA 设计为同 DSA 一起使用的，它对长度小于 264 的输入，产生长度为 160bit 的散列值，因此抗穷举性更好。SHA-1 设计时基于和 MD4 相同原理,并且模仿了该算法。SHA-1 的安全性在 2010 年以后已经不被大多数的加密场景所接受。2017 年荷兰密码学研究小组 CWI 和 Google 正式宣布攻破了 SHA-1。

SHA-2 由美国国家安全局研发，由美国国家标准与技术研究院（NIST）在 2001 年发布。属于 SHA 算法之一，是 SHA-1 的后继者。包括 SHA-224、SHA-256、SHA-384、SHA-512、SHA-512/224、SHA-512/256。SHA-256 和 SHA-512 是很新的杂凑函数，前者以定义一个 word 为 32 位元，后者则定义一个 word 为 64 位元。它们分别使用了不同的偏移量，或用不同的常数，然而，实际上二者结构是相同的，只在循环执行的次数上有所差异。SHA-224 以及 SHA-384 则是前述二种杂凑函数的截短版，利用不同的初始值做计算。

SHA-3 第三代安全散列算法之前名为 Keccak 算法，Keccak 使用海绵函数，此函数会将资料与初始的内部状态做 XOR 运算，这是无可避免可置换的（inevitably permuted）。在最大的版本，算法使用的内存状态是使用一个 5×5 的二维数组，资料类型是 64 位的字节，总计 1600 比特。缩版的算法使用比较小的，以 2 为幂次的字节大小 w 为 1 比特，总计使用 25 比特。除了使用较小的版本来研究加密分析攻击，比较适中的大小（例如从 w=4 使用 100 比特，到 w=32 使用 800 比特）则提供了比较实际且轻量的替代方案。

6.5. 对称密钥算法

对称密钥算法（Symmetric-key algorithm）又称为对称加密、私钥加密、共享密钥加密，是密码学中的一类加密算法。这类算法在加密和解密时使用相同的密钥，或是使用两个可以简单地相互推算的密钥。事实上，这组密钥成为在两个或多个成员间的共同秘密，以便维持专属的通信联系。与公开密钥加密相比，要求双方获取相同的密钥是对称密钥加密的主要缺点之一。

常见的对称加密算法有 AES、ChaCha20、3DES、Salsa20、DES、Blowfish、IDEA、RC5、RC6、Camellia 等。

对称加密的速度比公钥加密快很多，在很多场合都需要对称加密。

6.6. 非对称加密算法

非对称式密码学（Asymmetric cryptography）也称公开密钥密码学（Public-key cryptography），是密码学的另一类加密算法，它需要两个密钥，一个是公开密钥，另一个是私有密钥。公钥用作加密，私钥则用作解密。使用公钥把明文加密后所得的密文，只能用相对应的私钥才能解密并得到原本的明文，最初用来加密的公钥不能用作解密。由于加密和解密需要两个不同的密钥，故被称为非对称加密，不同于加密和解密都使用同一个密钥的对称加密。

公钥可以公开，可任意向外发布，私钥不可以公开，必须由用户自行严格秘密保管，绝不透过任何途径向任何人提供，也不会透露给被信任的要通信的另一方。

常用的非对称加密算法是 RSA 算法。

6.7. 哈希链

哈希链是一种由单个密钥或密码生成多个一次性密钥或密码的一种方法。哈希链是将密码学中的哈希函数 循环地用于一个字符串。（即将所得哈希值再次传递给哈希函数得至其哈希值）。

例：，是一个长度为 4 哈希链，记为：。

相比较而言，一个提供身份验证的服务器储存哈希字符串，比储存纯文本密码，更能防止密码在传输或储存时被泄露。举例来说，一个服务器一开始存储了一个由用户提供的哈希值 。进行身份验证时，用户提供给服务器 。服务器计算 即 ，并与已储存的哈希值 进行比较。然后服务器将存储 以用来对用户进行下次验证。

窃听者即使嗅探到 送交服务器，也无法将 用来认证，因为现在服务器验证算法传入的参数是 。由于安全的哈希函数有一种单向的加密属性，对于想要算出前一次哈希值的窃听者来说它的值是不可逆的。在本例中，用户在整个哈希链用完前可以验证 1000 次之多。每次哈希值是不同的，不能被攻击者再次使用。

7. 缓存淘汰策略

服务器常用缓存提升数据访问性能，但由于缓存容量有限，当缓存容量到达上限，就需要淘汰部分缓存数据挪出空间，这样新数据才可以添加进来。好的缓存应该是在有限的内存空间内尽量保持最热门的数据在缓存中，以提高缓存的命中率，因此如何淘汰数据有必要进行一番考究。缓存淘汰有多种策略，可以根据不同的业务场景选择不同淘汰的策略。

7.1. FIFO

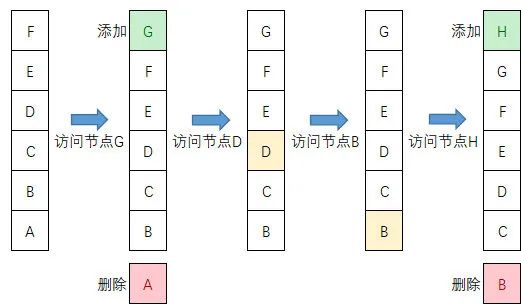
FIFO（First In First Out）是一种先进先出的数据缓存器，先进先出队列很好理解，当访问的数据节点不在缓存中时，从后端拉取节点数据并插入在队列头，如果队列已满，则淘汰最先插入队列的数据。

假设缓存队列长度为 6，过程演示如下：

7.2. LRU

LRU（Least recently used）是最近最少使用缓存淘汰算法，可它根据数据的历史访问记录来进行淘汰数据，其核心思想认为最近使用的数据是热门数据，下一次很大概率将会再次被使用。而最近很少被使用的数据，很大概率下一次不再用到。因此当缓存容量的满时候，优先淘汰最近很少使用的数据。因此它与 FIFO 的区别是在访问数据节点时，会将被访问的数据移到头结点。

假设缓存队列长度为 6，过程演示如下：

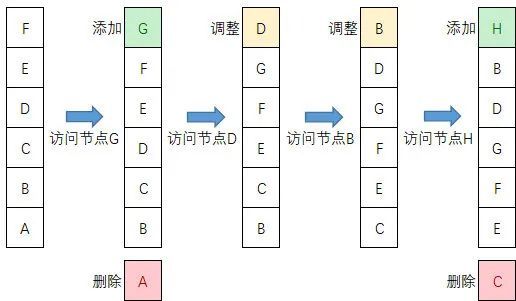
LRU 算法有个缺陷在于对于偶发的访问操作，比如说批量查询某些数据，可能使缓存中热门数据被这些偶发使用的数据替代，造成缓存污染，导致缓存命中率下降。

7.3. LFU

LFU 是最不经常使用淘汰算法，其核心思想认为如果数据过去被访问多次，那么将来被访问的频率也更高。LRU 的淘汰规则是基于访问时间，而 LFU 是基于访问次数。LFU 缓存算法使用一个计数器来记录数据被访问的次数，最低访问数的条目首先被移除。

假设缓存队列长度为 4，过程演示如下：

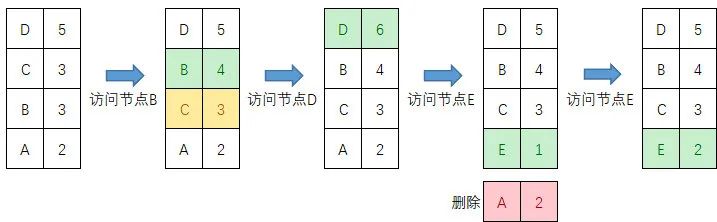
LFU 能够避免偶发性的操作导致缓存命中率下降的问题，但它也有缺陷，比如对于一开始有高访问率而之后长时间没有被访问的数据，它会一直占用缓存空间，因此一旦数据访问模式改变，LFU 可能需要长时间来适用新的访问模式，即 LFU 存在历史数据影响将来数据的"缓存污染"问题。另外对于对于交替出现的数据，缓存命中不高。

7.4. LRU-K

无论是 LRU 还是 LFU 都有各自的缺陷，LRU-K 算法更像是结合了 LRU 基于访问时间和 LFU 基于访问次数的思想，它将 LRU 最近使用过 1 次的判断标准扩展为最近使用过 K 次，以提高缓存队列淘汰置换的门槛。LRU-K 算法需要维护两个队列：访问列表和缓存列表。LRU 可以认为是 LRU-K 中 K 等于 1 的特化版。

LRU-K 算法实现可以描述为：

1. 数据第一次被访问，加入到访问列表，访问列表按照一定规则（如 FIFO，LRU）淘汰。

2. 当访问列表中的数据访问次数达到 K 次后，将数据从访问列表删除，并将数据添加到缓存列表头节点，如果数据已经在缓存列表中，则移动到头结点。

3. 若缓存列表数据量超过上限，淘汰缓存列表中排在末尾的数据，即淘汰倒数第 K 次访问离现在最久的数据。

假设访问列表长度和缓存列表长度都为 4，K=2，过程演示如下：

LRU-K 具有 LRU 的优点，同时能够降低缓存数据被污染的程度，实际应用可根据业务场景选择不同的 K 值，K 值越大，缓存列表中数据置换的门槛越高。

7.5. Two queues

Two queues 算法可以看做是 LRU-K 算法中 K=2，同时访问列表使用 FIFO 淘汰算法的一个特例。如下图所示：

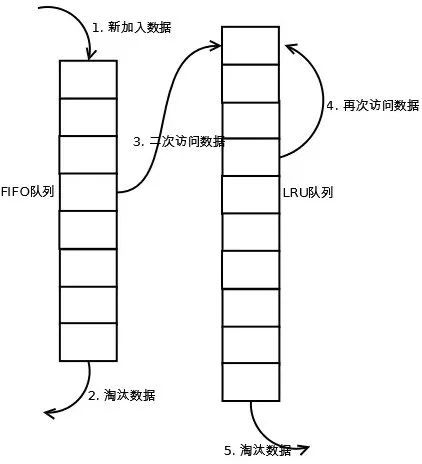
7.6. LIRS

LIRS（Low Inter-reference Recency Set）算法将缓存分为两部分区域：热数据区与冷数据区。LIRS 算法利用冷数据区做了一层隔离，目的是即使在有偶发性的访问操作时，保护热数据区的数据不会被频繁地被置换，以提高缓存的命中。

LIRS 继承了 LRU 根据时间局部性对冷热数据进行预测的思想，并在此之上 LIRS 引入了两个衡量数据块的指标：

1. IRR（Inter-Reference Recency）：表示数据最近两次访问之间访问其它数据的非重复个数

2. R （Recency）：表示数据最近一次访问到当前时间内访问其它数据的非重复个数，也就是 LRU 的维护的数据。

如下图，从左往右经过以下 8 次访问后，A 节点此时的 IRR 值为 3，R 值为 1。

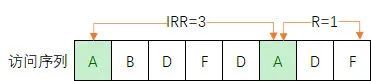
IRR 可以由 R 值计算而来，具体公式为：IRR=上一时刻的 R-当前时刻的 R，如上图当前时刻访问的节点是 F，那么当前时刻 F 的 R 值为 0，而上一个 F 节点的 R 值为 2，因此 F 节点的 IRR 值为 2。

LIRS 动态维护两个集合：

1. LIR（low IRR block set）：具有较小 IRR 的数据块集合，可以将这部分数据块理解为热数据，因为 IRR 低说明访问的频次高。

2. HIR（high IRR block set）：具有较高 IRR 的数据块集合，可以将这部分数据块理解为冷数据。

LIR 集合所有数据都在缓存中，而 HIR 集合中有部分数据不在缓存中，但记录了它们的历史信息并标记为未驻留在缓存中，称这部分数据块为 nonresident-HIR，另外一部分驻留在缓存中的数据块称为 resident-HIR。

LIR 集合在缓存中，所以访问 LIR 集合的数据是百分百会命中缓存的。而 HIR 集合分为 resident-HIR 和 nonresident-HIR 两部分，所以会遇到未命中情况。当发生缓存未命中需要置换缓存块时，会选择优先淘汰置换 resident-HIR。如果 HIR 集合中数据的 IRR 经过更新比 LIR 集合中的小，那么 LIR 集合数据块就会被 HIR 集合中 IRR 小的数据块挤出并转换为 HIR。

LIRS 通过限制 LIR 集合的长度和 resident-HIR 集合长度来限制整体大小，假设设定 LIR 长度为 2，resident-HIR 长度为 1 的 LIRS 算法过程演示如下：

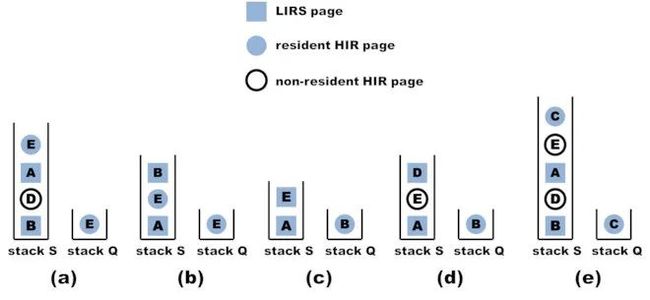
1. 所有最近访问的数据都放置在称为 LIRS 堆栈的 FIFO 队列中（图中的堆栈 S），所有常驻的 resident-HIR 数据放置在另一个 FIFO 队列中（图中的堆栈 Q）。

2. 当栈 S 中的一个 LIR 数据被访问时，被访问的数据会被移动到堆栈 S 的顶部，并且堆栈底部的任何 HIR 数据都被删除，因为这些 HIR 数据的 IRR 值不再有可能超过任何 LIR 数据了。例如，图（b）是在图（a）上访问数据 B 之后生成的。

3. 当栈 S 中的一个 resident-HIR 数据被访问时，它变成一个 LIR 数据，相应地，当前在栈 S 最底部的 LIR 数据变成一个 HIR 数据并移动到栈 Q 的顶部。例如，图（c）是在图（a）上访问数据 E 之后生成的。

4. 当栈 S 中的一个 nonresident-HIR 数据被访问时，它变成一个 LIR 数据，此时将选择位于栈 Q 底部的 resident-HIR 数据作为替换的牺牲品，降级为 nonresident-HIR，而栈 S 最底部的 LIR 数据变成一个 HIR 数据并移动到栈 Q 的顶部。例如，图（d）是在图（a）上访问数据 D 之后生成的。

5. 当访问一个不在栈 S 中的数据时，它会成为一个 resident-HIR 数据放入栈 Q 的顶部，同样的栈 Q 底部的 resident-HIR 数据会降级为 nonresident-HIR。例如，图（e）是在图（a）上访问数据 C 之后生成的。

解释一下当栈 S 中的一个 HIR 数据被访问时，它为什么一定会变成一个 LIR 数据：这个数据被访问时，需要更新 IRR 值（即为当前的 R 值），使用这个新的 IRR 与 LIR 集合数据中最大的 R 值进行比较（即栈 S 最底部的 LIR 数据），新的 IRR 一定会比栈 S 最底部的 LIR 数据的 IRR 小（因为栈 S 最底部的数据一定是 LIR 数据，步骤 2 已经保证了），所以它一定会变成一个 LIR 数据。

7.7. MySQL InnoDB LRU

MySQL InnoDB 中的 LRU 淘汰算法采用了类似的 LIRS 的分级思想，它的置换数据方式更加简单，通过判断冷数据在缓存中存在的时间是否足够长（即还没有被 LRU 淘汰）来实现。数据首先进入冷数据区，如果数据在较短的时间内被访问两次或者以上，则成为热点数据进入热数据区，冷数据和热数据部分区域内部各自还是采用 LRU 替换算法。

MySQL InnoDB LRU 算法流程可以描述为：

1. 访问数据如果位于热数据区，与 LRU 算法一样，移动到热数据区的头结点。

2. 访问数据如果位于冷数据区，若该数据已在缓存中超过指定时间，比如说 1s，则移动到热数据区的头结点；若该数据存在时间小于指定的时间，则位置保持不变。

3. 访问数据如果不在热数据区也不在冷数据区，插入冷数据区的头结点，若冷数据缓存已满，淘汰尾结点的数据。

8. 基数集与基数统计

基数集即不重复元素的集合，基数统计即统计基数集中元素的个数。比如说 18 号晚微信视频号西城男孩直播夜的累积观看人数统计就是一个基数统计的应用场景。

8.1. 哈希表

哈希表是根据关键码（Key）而直接进行访问的数据结构，它把关键码映射到一个有限的地址区间上存放在哈希表中，这个映射函数叫做散列函数。哈希表的设计最关键的是使用合理的散列函数和冲突解决算法。

好的散列函数应该在输入域中较少出现散列冲突，数据元素能被更快地插入和查找。常见的散列函数算法有：直接寻址法，数字分析法，平方取中法，折叠法，随机数法，除留余数法等。

然而即使再好的散列函数，也不能百分百保证没有冲突，因此必须要有冲突的应对方法，常见的冲突解决算法有：

1. 开放定址法：从发生冲突的那个单元起，按照一定的次序，从哈希表中找到一个空闲的单元。然后把发生冲突的元素存入到该单元的一种方法。开放定址法需要的表长度要大于等于所需要存放的元素。而查询一个对象时，则需要从对应的位置开始向后找，直到找到或找到空位。根据探查步长决策规则不同，开放定址法中一般有：线行探查法（步长固定为 1，依次探查）、平方探查法（步长为探查次数的平方值）、双散列函数探查法（步长由另一个散列函数计算决定）。

2. 拉链法：在每个冲突处构建链表，将所有冲突值链入链表（称为冲突链表），如同拉链一般一个元素扣一个元素。

3. 再哈希法：就是同时构造多个不同的哈希函数，当前面的哈希函数发生冲突时，再用下一个哈希函数进行计算，直到冲突不再产生。

4. 建立公共溢出区：哈希表分为公共表和溢出表，当溢出发生时，将所有溢出数据统一放到溢出区。

使用哈希表统计基数值即将所有元素存储在一个哈希表中，利用哈希表对元素进行去重，并统计元素的个数，这种方法可以精确的计算出不重复元素的数量。

但使用哈希表进行基数统计，需要存储实际的元素数据，在数据量较少时还算可行，但是当数据量达到百万、千万甚至上亿时，使用哈希表统计会占用大量的内存，同时它的查找过滤成本也很高。如 18 号晚微信视频号西城男孩直播夜有 2000 万多的用户观看，假设记录用户的 id 大小需要 8 字节，那么使用哈希表结构至少需要 152.6M 内存，而为了降低哈希冲突率，提高查找性能，实际需要开辟更大的内存空间。

8.2. 位图（Bitmap）

位图就是用每一比特位来存放真和假状态的一种数据结构，使用位图进行基数统计不需要去存储实际元素信息，只需要用相应位置的 1bit 来标识某个元素是否出现过，这样能够极大地节省内存。

如下图所示，假设要存储的数据范围是 0-15，我们只需要使用 2 个字节组建一个拥有 16bit 位的比特数组，所有 bit 位的值初始化为 0，需要存储某个值时只需要将相应位置的的 bit 位设置为 1，如下图存储了{2,5,6,9,11,14}六个数据。

假设观看西城男孩直播的微信 id 值域是[0-2000 万]，采用位图统计观看人数所需要的内存就只需 2.38M 了。

位图统计方式内存占用确实大大减少了，但位图占用的内存和元素的值域有关，因为我们需要把值域映射到这个连续的大比特数组上。实际上观看西城男孩直播的微信 id 不可能是连续的 2000 万个 id 值，而应该按微信的注册量级开辟长度，可能至少需要 20 亿的 bit 位（238M 内存）。

8.3. 布隆过滤器

位图的方式有个很大的局限性就是要求值域范围有限，比如我们统计观看西城男孩直播的微信 id 总计 2000 万个，但实际却需要按照微信 id 范围上限 20 亿来开辟空间，假如有一个完美散列函数，能正好将观看了直播的这 2000 万个微信 id 映射成[0-2000 万]的不重复散列值，而其余没有观看直播的 19.8 亿微信 id 都被映射为超过 2000 万的散列值，那事情就好办了，但事实是我们无法提前知道哪 2000 万的微信号会观看直播，因此这样的散列函数是不可能存在的。

但这个思想是对的，布隆过滤器就是类似这样的思想，它能将 20 亿的 id 值映射到更小数值范围内，然后使用位图来记录元素是否存在，因为值域范围被压缩了，必然会存在大面积的冲突，为了降低冲突导致的统计错误率，它通过 K 个不同的散列函数将元素映射成一个位图中的 K 个 bit 位，并把它们都置为 1，只有当某个元素对应的这 K 个 bit 位同时为 1，才认为这个元素已经存在过。

假设 K=3，3 个哈希函数将数据映射到 0-15 的位图中存储，过程演示如下：

类似百分比近似排序，布隆过滤器也是牺牲一定的精确度来换取高性能的做法。它仍然存在一定的错误率，不能保证完全准确，比如上图示例中，假设接下来要插入数据 123，它通过 3 个哈希函数分别被映射为：{2,3,6}，此时会误判为 123 已经存在了，将过滤掉该数据的统计。

但实际上只要 K 值和位图数组空间设置合理，就能保证错误率在一定范围，这对于大数据量的基数统计，完全能接受这样的统计误差。

8.4. 布谷鸟过滤器

布谷鸟过滤器是另外一种通过牺牲一定的精确度来换取高性能的做法，也是非常之巧妙。在解释布谷鸟过滤器之前我们先来看下布谷鸟哈希算法。

布谷鸟哈希算法是 8.1 节中讲到的解决哈希冲突的另一种算法，它的思想来源于布谷鸟“鸠占鹊巢”的生活习性。布谷鸟哈希算法会有两个散列函数将元素映射到哈希表的两个不同位置。如果两个位置中有一个位置为空，那么就可以将元素直接放进去。但是如果这两个位置都满了，它就随机踢走一个，然后自己霸占了这个位置。

被踢走的那个元素会去查看它的另外一个散列值的位置是否是空位，如果是空位就占领它，如果不是空位，那就把受害者的角色转移出去，挤走对方，让对方再去找安身之处，如此循环直到某个元素找到空位为止。布谷鸟哈希算法有个缺点是当空间本身很拥挤时，出现“鸠占鹊巢”的现象会很频繁，插入效率很低，一种改良的优化方案是让每个散列值对应的位置上可以放置多个元素。

8.1 节讲到，哈希表可以用来做基数统计，因此布谷鸟哈希表当然也可以用来基数统计，而布谷鸟过滤器基于布谷鸟哈希算法来实现基数统计，布谷鸟哈希算法需要存储数据的整个元素信息，而布谷鸟过滤器为了减少内存，将存储的元素信息映射为一个简单的指纹信息，例如微信的用户 id 大小需要 8 字节，我们可以将它映射为 1 个字节甚至几个 bit 的指纹信息来进行存储。

由于只存储了指纹信息，因此谷鸟过滤器的两个散列函数的选择比较特殊，当一个位置上的元素被挤走之后，它需要通过指纹信息计算出另一个对偶位置（布谷鸟哈希存储的是元素的完整信息，必然能找到另一个散列值位置），因此它采用异或的方式达到目的，公式如下：

h1(x) = hash(x)
h2(x) = h1(x) ⊕ hash(x的指纹)

位置 h2 可以通过位置 h1 和 h1 中存储的指纹信息计算出来，同样的位置 h1 也可以通过 h2 和指纹信息计算出来。

布谷鸟过滤器实现了哈希表过滤和基数统计的能力，同时存储元素信息改为存储更轻量指纹信息节约了内存，但它损失了一些精确度，比如会出现两个元素的散列位置相同，指纹也正好相同的情况，那么插入检查会认为它们是相等的，只会统计一次。但同样这个误差率是可以接受的。

8.5. HyperLogLog

说到基数统计，就不得不提 Redis 里面的 HyperLogLog 算法了，前文所说的哈希表，位图，布隆过滤器和布谷鸟过滤器都是基于记录元素的信息并通过过滤（或近似过滤）相同元素的思想来进行基数统计的。

而 HyperLogLog 算法的思想不太一样，它的基础是观察到可以通过计算集合中每个数字的二进制表示中的前导零的最大数目来估计均匀分布的随机数的多重集的基数。如果观察到的前导零的最大数目是 n，则集合中不同元素的数量的估计是 。

怎么理解呢？其实就是运用了数学概率论的理论，以抛硬币的伯努利试验为例，假设一直尝试抛硬币，直到它出现正面为止，同时记录第一次出现正面时共尝试的抛掷次数 k，作为一次完整的伯努利试验。那么对于 n 次伯努利试验，假设其中最大的那次抛掷次数为 。结合极大似然估算的方法，n 和 中存在估算关联关系即：。

对应于基数统计的场景，HyperLogLog 算法通过散列函数，将数据转为二进制比特串，从低位往高位看，第一次出现 1 的时候认为是抛硬币的正面，因此比特串中前导零的数目即是抛硬币的抛掷次数。因此可以根据存入数据中，转化后的二进制串集中最大的首次出现 1 的位置 来估算存入了多少不同的数据。

这种估算方式存在一定的偶然性，比如当某次抛硬币特别不幸时，抛出了很大的值，数据会偏差的厉害，为了降低这种极端偶然性带来的误差影响，在 HyperLogLog 算法中，会将集合分成多个子集（分桶计算），分别计算这些子集中的数字中的前导零的最大数量，最后使用调和平均数的计算方式将所有子集的这些估计值计算为全集的基数。例如 redis 会分为 16384 个子集进行分桶求平均统计。

9. 其他常用算法

9.1. 时间轮定时器

定时器的实现方式有很多，比如用有序链表或堆都可以实现，但是他们或插入或运行或删除的性能不太好。时间轮定时器是一种插入，运行和删除都比较理想的定时器。

时间轮定时器将按照到期时间分桶放入缓存队列中，系统只需按照每个桶到期顺序依次执行到期的时间桶节点中的所有定时任务。

如下图所示：

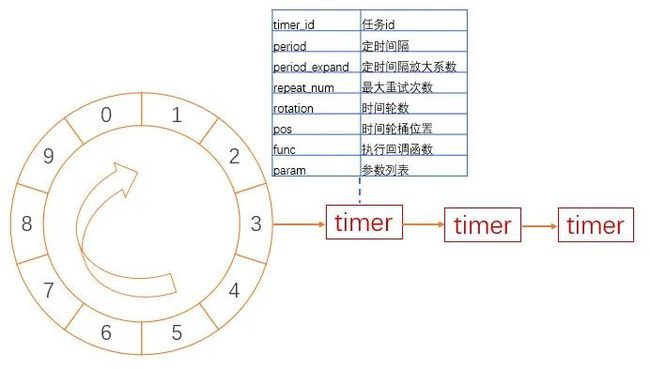
而针对定时任务时间跨度大，且精度要求较高的场景，使用单层时间轮消耗的内存可能比较大，因此还可以进一步优化为采用层级时间轮来实现，层级时间轮就类似我们的时钟，秒针转一圈后，分针才进一格的原理，当内层时间轮运转完一轮后，外层时间轮进一格，接下来运行下一格的内层时间轮。

9.2. 红包分配

算法很简洁，该算法没有预先随机分配好红包金额列表，而是在每个用户点击抢红包时随机生成金额，该算法只需传入当前剩余的总金额和剩余需要派发的总人数，算法的基本原理是以剩余单个红包的平均金额的 2 倍为上限，随机本次分配的金额。

这个算法的公平性在于每个领红包的人能领取到的金额是从 0 到剩余平均金额的 2 倍之间的随机值，所以期望就是剩余平均金额，假设 100 元发给 5 个人，那么第一个人领取到的期望是 20 元，第 2 个人领取到的期望是（100-20）/ 4 = 20 元，通过归纳法可以证明每个人领取到的期望都是 20 元。但是由于每个人领取到的金额随机范围是不一样的，如第一个人能领取到的范围是 0 到 40 元，而最后一个人能领取到的范围是 0 到 100 元，因此方差跟领取的顺序是有关系。这也告诉我们抢微信红包想稳的人可以先抢，想博的人可以后抢。

这种分配算法的好处是无状态化，不需要在创建红包时预先分配并存储金额列表，在某些场景可能会对性能带来好处。

9.3. 有缘再续

优秀的算法还有很多，有缘再续。

10. 总结

笔者曾经写过一篇《服务器开发设计词汇宝典》，讲述了一些后台程序架构和系统方面的设计知识，如果把架构设计比做程序员的内功修炼的话，那么算法就是战斗中的招式，选择合适的算法能让你的代码化繁为简，或高效或优雅，见招拆招，起到四两拨千斤的效果的同时震撼心灵。

很多算法的思想都有一些共通性，他们用到的基础思想都有相似之处，如随机，分治递归，多策略相结合，一次不行再来一次等思想。比如随机，这个在服务器开发设计中随处可见的策略，yyds，随机带来的是一种个体偶然性与总体必然性的结合，在 jump consistent hash 算法，跳表排序算法、带权重的 A-ExpJ 算法蓄水池抽样等算法中都使用了随机跳跃的思想，实现了在无需统计状态数据的情况下，利用随机的整体均衡性来保证算法正确性的同时极大的简化了算法和提高了效率。

学习和研究优秀的算法目的是希望能在实际应用场景中做到灵活运用，取长补短，甚至能结合不同算法思想启发创造出适合各种问题场景的算法策略。

由于个人水平有限，文中难免有所纰漏，欢迎指正。

参考文章

1. 《The Power of Two Random Choices》

2. 《The Art of Computer Programming （vol. 2_ Seminumerical Algorithms） （3rd ed.）》

3. 《Fisher–Yates shuffle》wikipedia

4. 《Random Sampling with a Reservoir》JEFFREY SCOTT VITTER

5. 《Weighted Random Sampling》（Efraimidis, Spirakis）

6. 《Weighted random sampling with a reservoir》（Efraimidis, Spirakis）

7. 《Reservoir sampling》wikipedia

8. 《十大经典排序算法》菜鸟教程

9. 《多路平衡归并排序算法》

10. 《TDigest 算法原理》

11. 《ElasticSearch 如何使用 TDigest 算法计算亿级数据的百分位数？》

12. 《分位数算法总结》

13. 《Handling Overload》

14. 《zigzag 算法详解》

15. 《数据序列化格式》wikipedia

16. 《markdown》百度百科

17. 《拥抱 protobuf，迎接 TDR 2.0 时代》 km 文章

18. 《Compress》https://gitee.com/yu120/compress

19. 《无损压缩算法》wikipedia

20. 《LZ77 与 LZ78》 wikipedia

21. 《公开密钥加密》wikipedia

22. 《哈希链》wikipedia

23. 《常用缓存淘汰算法 LFU/LRU/ARC/FIFO/MRU》

24. 《LIRS caching algorithm》wikipedia

25. 《缓存淘汰算法 LIRS 原理与实现》

26. 《MySQL 5.7 Reference Manual》

27. 《布隆过滤器过时了，未来属于布谷鸟过滤器？》

28. 《HyperLogLog 算法的原理讲解以及 Redis 是如何应用它的》

29. 《关于基数统计》

30. 《算法导论（第 2 版）》

31. 其他网络资料

最近好文：

微信图片翻译技术优化之路

C++ 智能指针最佳实践&源码分析

Golang 并发编程指南