你好_Ä

ACM2021辽宁省赛：CDEFGILM

C-传染病统计_

问题解析

一开始没注意到n只有8。。。当1e5的范围来写的。

这题就是说，所有相隔距离小于等于2的是一个集体，然后我们要选一个集体感染病毒，问最多的感染人数和最小的感染人数。

先对所有人进行升序排序（因为不知道给的输入是不是有序的）。然后遍历一遍数组，把相隔距离不超过2的都当作一个集体，如果B和A的距离超过2了，说明B是另一个集体，我们重新计算。在此过程中维护集体人数的最大值和最小值。

分别输出最小值和最大值即可。

时间复杂度：（T*nlogn）;

AC代码

#include
using namespace std;
#include
#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#pragma GCC optimize(2)
#pragma GCC optimize(3)

#define endl '\n'
#define int ll
#define PI acos(-1)
#define INF 0x3f3f3f3f
typedef long long ll;
typedef unsigned long long ull;
typedef pairPII;
const int N = 1e6 + 50;

void solve()
{
    int n;
    cin >> n;
    vectorv(n);
    for (int i = 0; i < n; i++)cin >> v[i];
    sort(v.begin(), v.end());
    int mx = 0, mn = 1e9, len = 1;
    for (int i = 1; i < n; i++)
    {
        if (v[i] - v[i - 1] <= 2)len++;
        else
        {
            mx = max(mx, len);
            mn = min(mn, len);
            len = 1;
        }
    }
    mx = max(mx, len);
    mn = min(mn, len);
    cout << mn << " " << mx << endl;
}

signed main()
{

    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    cin >> t;

    while (t--)
    {
        solve();
    }
    return 0;
}

D-阿强与网格

问题解析

一开始下意识的想BFS，后来发现根本不用那么麻烦（而且也过不了）。

题目已经给定了我们每次操作所花成本，我们可以根据x和y的大小，与网格的形状直接计算得出结果，为了方便，我们认定n比m大：

如果网格是n *1的形状，此时显然只能用x的方式移动，成本为：*（n-1）x;
因为y走一步等于x走两步，所以如果x的两倍小于等于y，我们直接用x走，成本为：*（n+m-2）x

剩下的情况，我们显然是能用y走就用y走，问题是y该怎么走呢？

一开始想着先对角线移动到底部，然后剩下的用x平移过去：（红色路线）

后来发现，其实剩下的位置也是可以斜着走的：（蓝色路线）

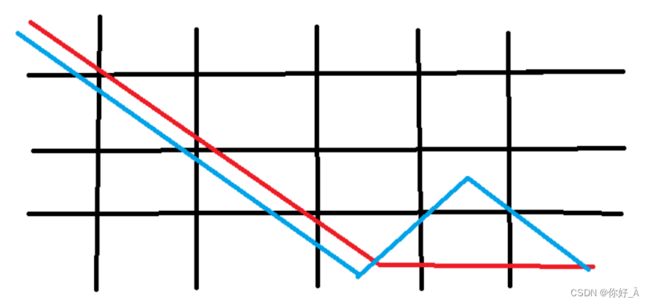
只不过这么走有约束，即到了底边后，距离终点的距离如果是奇数，则会停在终点的前一格，而这时我们只能用x走了：（橙色路线）

那么对于其它的情况：我们先走m次y，如果距离终点的距离：n-m是奇数，我们走了（n-m-1)次y后，还要走一次x，成本为：m*y+(n-m-1) * y+x；如果n-m是偶数，我们直接全走y即可，成本为：m*y+(n-m) * y.

AC代码

#include
using namespace std;
#include
#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#pragma GCC optimize(2)
#pragma GCC optimize(3)

#define endl '\n'
#define int ll
#define PI acos(-1)
#define INF 0x3f3f3f3f
typedef long long ll;
typedef unsigned long long ull;
typedef pairPII;
const int N = 4e5 + 50;

void solve()
{
    int n, m, x, y,ans;
    cin >> n >> m >> x >> y;
    //为了方便，我们保证n比m大
    if(n> t;

    while (t--)
    {
        solve();
    }
    return 0;
}

E-生活大爆炸

问题解析

这道题主要思路就是我们高中就学过的组合数计算。

男生有n人，女生有m人，需要组成总人数为t的队伍，其中男生人数不能少于4人，女生人数不能少于1人。

那么可能的排列组合就是：4个男生和t-4名女生，5个男生和t-5名女生，……，t-1名男生和1名女生。

对于第一个组合来说，就是n个男生中随机选出4个，搭配上m个女生中随机选出t-4个，即：C(n,4)*C(m,t-4)。其余的以此类推，把所有的组合数相加即可。

AC代码

#include
using namespace std;
#include
#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#pragma GCC optimize(2)
#pragma GCC optimize(3)

#define endl '\n'
#define int ll
#define PI acos(-1)
#define INF 0x3f3f3f3f
typedef long long ll;
typedef unsigned long long ull;
typedef pairPII;
const int N = 4e5 + 50;

int C[70][70];
void init()
{
    for (int i = 0; i <= 70; i++)
        for (int j = 0; j <= i; j++) {
            if (!j)
                C[i][j] = 1;
            else
                C[i][j] = C[i - 1][j - 1] + C[i - 1][j];
        }
}

void solve()
{
    int n, m, t;
    cin >> n >> m >> t;
    init();
    int res = 0;
    for (int i = 4; i <= min(n, t - 1); i++)
    {
        res += C[n][i] * C[m][t - i];
    }
    cout << res;
}

signed main()
{

    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    //cin >> t;

    while (t--)
    {
        solve();
    }
    return 0;
}

F-Capslock

问题解析

只要看第2到第n个字符是不是都是大写字母，如果是，遍历一遍数组把大写字母变成小写字母，把小写字母变成大写字母。如果不是，直接原样输出。

AC代码

#include
using namespace std;
#include
#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#pragma GCC optimize(2)
#pragma GCC optimize(3)

#define endl '\n'
#define int ll
#define PI acos(-1)
#define INF 0x3f3f3f3f
typedef long long ll;
typedef unsigned long long ull;
typedef pairPII;
const int N = 1e6 + 50;

void solve()
{
    string s;
    cin >> s;
    int n = s.size();
    bool flag = true;
    for (int i = 1; i < n; i++)
    {
        if (!(s[i] >= 'A' && s[i] <= 'Z'))
        {
            flag = false;
            break;
        }
        
    }
    if (!flag)
    {
        cout << s << endl;
        return;
    }
    if (s[0] >= 'A' && s[0] <= 'Z')
    {
        s[0] += 32;
    }
    else s[0] -= 32;
    for (int i = 1; i < n; i++)
    {
        s[i] += 32;
    }
    cout << s;
}

signed main()
{

    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    //cin >> t;

    while (t--)
    {
        solve();
    }
    return 0;
}

G-字节类型

问题解析

可以用字符串来接收输入。

根据字符串的长度和转换成整数后的大小进行比较即可。

如果担心longlong会炸，就用unsigned long long来存储结果。字符串长度要是大于19，直接就是BigInteger。

AC代码

#include
using namespace std;
#include
#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#pragma GCC optimize(2)
#pragma GCC optimize(3)

#define endl '\n'
#define int ll
#define PI acos(-1)
#define INF 0x3f3f3f3f
typedef long long ll;
typedef unsigned long long ull;
typedef pairPII;
const int N = 1e6 + 50;

ull check(string s)
{
    ull num = 0;
    int n = s.size();
    for (int i = 0; i < n; i++)
    {
        num *= 10;
        num += s[i] - '0';
    }
    return num;
}

void solve()
{
    string s;
    cin >> s;
    int n = s.size();
    if (n > 19)cout << "BigInteger" << endl;
    else if (n <= 3)
    {
        int num = stoi(s);
        if (num <= 127)cout << "byte" << endl;
        else cout << "short" << endl;
    }
    else if (n <= 5)
    {
        int num = stoi(s);
        if (num <= 32767)cout << "short" << endl;
        else cout << "int" << endl;
    }
    else if (n <= 10)
    {
        int num = stoi(s);
        if (num <= 2147483647)cout << "int" << endl;
        else cout << "long" << endl;
    }
    else if (n <= 19)
    {
        ull num = check(s);
        if (num <= 9223372036854775807)cout << "long" << endl;
        else cout << "BigInteger" << endl;
    }
}

signed main()
{

    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    //cin >> t;

    while (t--)
    {
        solve();
    }
    return 0;
}

I-完美主义

问题解析

开一个单点修改+区间查询的线段树。

st[k]表示，st[k]为true，表示当前区间是完美区间，反之不是；
right[k]表示当前区间最右边的元素；
left[k]表示当前区间最右边的元素；

对于一个区间，如果它的左右子区间的st都为true，且左区间的right小于等于右区间的left，那么当前区间也是一个true；反之是false。由此类推，我们每次更新时，只要维护区间的left和right，再根据他们的大小判断st的值，就可以快速得出当前区间是否是完美的。

AC代码

#include
using namespace std;
#include
#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#pragma GCC optimize(2)
#pragma GCC optimize(3)

#define endl '\n'
#define int ll
#define PI acos(-1)
#define INF 0x3f3f3f3f
typedef long long ll;
typedef unsigned long long ull;
typedef pairPII;
const int N = 4e5 + 50;

int myleft[4 * N], myright[4 * N], a[N];
bool st[4 * N];
void build_tree(int k, int l, int r)
{
    if (l == r)
    {
        myleft[k] = a[l];
        myright[k] = a[l];
        st[k] = true;
        return;
    }
    int m = (l + r) / 2;
    build_tree(k + k, l, m);
    build_tree(k + k + 1, m + 1, r);
    if (myleft[k + k + 1] >= myright[k + k])
    {
        st[k] = st[k + k] && st[k + k + 1];
    }
    else st[k] = false;
    myleft[k] = myleft[k + k];
    myright[k] = myright[k + k + 1];
}

void revise(int k, int l, int r, int x, int y)
{
    if (l == r)
    {
        myleft[k] = y;
        myright[k] = y;
        return;
    }
    int m = (l + r) / 2;
    if (x <= m)revise(k + k, l, m, x, y);
    else revise(k + k + 1, m + 1, r, x, y);
    if (myleft[k + k + 1] >= myright[k + k])
    {
        st[k] = st[k + k] && st[k + k + 1];
    }
    else st[k] = false;
    myleft[k] = myleft[k + k];
    myright[k] = myright[k + k + 1];
}

//对于pair>，first表示这个区间的st。
//second。first是left；second。second是right
pair> calc(int k, int l, int r, int x, int y)
{
    if (l == x && r == y)return { st[k],{myleft[k],myright[k]} };
    int m = (l + r) / 2;
    if (y <= m)return calc(k + k, l, m, x, y);
    else
        if (x > m)return calc(k + k + 1, m + 1, r, x, y);
        else
        {
            auto ans1 = calc(k + k, l, m, x, m);
            auto ans2 = calc(k + k + 1, m + 1, r, m + 1, y);
            if (ans1.first == false || ans2.first == false)
            {
                return { false,{-1,-1} };
            }
            else
            {
                if (ans1.second.second <= ans2.second.first)
                {
                    return { true,{ans1.second.first,ans2.second.second} };
                }
                else return { false,{-1,-1} };
            }
        }
}

void solve()
{
    int n, m, t, x, y;
    cin >> n >> m;
    for (int i = 1; i <= n; i++)cin >> a[i];
    build_tree(1, 1, n);
    while (m--)
    {
        cin >> t >> x >> y;
        if (t == 1)
        {
            revise(1, 1, n, x, y);
        }
        else
        {
            if (calc(1, 1, n, x, y).first)
            {
                cout << "Yes" << endl;
            }
            else cout << "No" << endl;
        }
    }
}

signed main()
{

    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    //cin >> t;

    while (t--)
    {
        solve();
    }
    return 0;
}

L-神奇的回答

问题解析

大于18的输出18，小于等于18的原样输出。

AC代码

#include
using namespace std;
#include
#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#pragma GCC optimize(2)
#pragma GCC optimize(3)

#define endl '\n'
#define int ll
#define PI acos(-1)
#define INF 0x3f3f3f3f
typedef long long ll;
typedef unsigned long long ull;
typedef pairPII;
const int N = 1e6 + 50;

void solve()
{
    int n;
    cin >> n;
    if (n >= 18)cout << 18 << endl;
    else cout << n << endl;
}

signed main()
{

    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    cin >> t;

    while (t--)
    {
        solve();
    }
    return 0;
}

M-比赛!

问题解析

拓扑排序。

根据每个人的回答，我们把它看成“A：BC”，转化成关系就是，B->A->C。我们以此来建图，同时记录每个点的入度。

建图之后来一遍拓扑排序，用一个字符串s来存储结果，因为入度为0的点，相当于它的前面没有别的选手，我们就可以把它加入到字符串的尾部。

如果拓扑排序后，所有的选手都在字符串里了，我们就把他输出；否则输出No Answer。

AC代码

#include
using namespace std;
#include
#include
#include
#include
#include 
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include

#pragma GCC optimize(2)
#pragma GCC optimize(3)

#define endl '\n'
#define int ll
#define PI acos(-1)
#define INF 0x3f3f3f3f
typedef long long ll;
typedef unsigned long long ull;
typedef pairPII;
const int N = 4e5 + 50;

vectorgraph[300];
unordered_mapmymap;
void solve()
{
    int n;
    cin >> n;
    string s;
    for (int i = 1; i <= n; i++)
    {
        cin >> s;
        graph[s[2]].push_back(s[0]);
        graph[s[0]].push_back(s[3]);
        if (!mymap.count(s[2]))mymap[s[2]] = 0;
        mymap[s[0]]++;
        mymap[s[3]]++;
    }
    queueque;
    string str;
    for (auto& i : mymap)
    {
        if (i.second == 0)
        {
            str += i.first;
            que.push(i.first);
        }
    }
    
    if (que.size() == 0)
    {
        cout << "No Answer" << endl;
        return;
    }
    while (!que.empty())
    {
        auto t = que.front();
        que.pop();
        bool flag = false;
        for (auto i : graph[t])
        {
            mymap[i]--;
            if (mymap[i] == 0)
            {
                str+=i;
                que.push(i);
            }
        }
    }
    if(mymap.size()!=str.size())
    {
        cout << "No Answer" << endl;
    }
    else cout << str << endl;
}

signed main()
{

    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);
    int t = 1;
    //cin >> t;

    while (t--)
    {
        solve();
    }
    return 0;
}

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
10月|愿你的青春不负梦想-读书笔记-01 Tracy的小书斋
本书的作者是俞敏洪，大家都很熟悉他了吧。俞敏洪老师是我行业的领头羊吧，也是我事业上的偶像。本日摘录他书中第一章中的金句：『一个人如果什么目标都没有，就会浑浑噩噩，感觉生命中缺少能量。能给我们能量的，是对未来的期待。第一件事，我始终为了进步而努力。与其追寻全世界的骏马，不如种植丰美的草原，到时骏马自然会来。第二件事，我始终有阶段性的目标。什么东西能给我能量？答案是对未来的期待。』读到这里的时候，我便
c++ 的iostream 和 c++的stdio的区别和联系黄卷青灯77 c++算法开发语言 iostream stdio
在C++中，iostream和C语言的stdio.h都是用于处理输入输出的库，但它们在设计、用法和功能上有许多不同。以下是两者的区别和联系：区别1.编程风格iostream（C++风格）：C++标准库中的输入输出流类库，支持面向对象的输入输出操作。典型用法是cin（输入）和cout（输出），使用>操作符来处理数据。更加类型安全，支持用户自定义类型的输入输出。#includeintmain(){in
《投行人生》读书笔记小蘑菇的树洞
《投行人生》----作者詹姆斯-A-朗德摩根斯坦利副主席40年的职业洞见-很短小精悍的篇幅，比较适合初入职场的新人。第一部分成功的职业生涯需要规划1.情商归为适应能力分享与协作同理心适应能力，更多的是自我意识，你有能力识别自己的情并分辨这些情绪如何影响你的思想和行为。2.对于初入职场的人的建议，细节，截止日期和数据很重要截止日期，一种有效的方法是请老板为你所有的任务进行优先级排序。和老板喝咖啡的好
【一起学Rust | 设计模式】习惯语法——使用借用类型作为参数、格式化拼接字符串、构造函数广龙宇一起学Rust #Rust设计模式 rust 设计模式开发语言
提示：文章写完后，目录可以自动生成，如何生成可参考右边的帮助文档文章目录前言一、使用借用类型作为参数二、格式化拼接字符串三、使用构造函数总结前言Rust不是传统的面向对象编程语言，它的所有特性，使其独一无二。因此，学习特定于Rust的设计模式是必要的。本系列文章为作者学习《Rust设计模式》的学习笔记以及自己的见解。因此，本系列文章的结构也与此书的结构相同（后续可能会调成结构），基本上分为三个部分
git常用命令笔记咩酱-小羊 git 笔记
###用习惯了idea总是不记得git的一些常见命令，需要用到的时候总是担心旁边站了人~~~记个笔记@_@，告诉自己看笔记不丢人初始化初始化一个新的Git仓库gitinit配置配置用户信息gitconfig--globaluser.name"YourName"gitconfig--globaluser.email"[email protected]"基本操作克隆远程仓库gitclone查看
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
509. 斐波那契数(每日一题) lzyprime
lzyprime博客(github)创建时间：2021.01.04qq及邮箱：2383518170leetcode笔记题目描述斐波那契数，通常用F(n)表示，形成的序列称为斐波那契数列。该数列由0和1开始，后面的每一项数字都是前面两项数字的和。也就是：F(0)=0，F(1)=1F(n)=F(n-1)+F(n-2)，其中n>1给你n，请计算F(n)。示例1：输入：2输出：1解释：F(2)=F(1)+
拥有断舍离的心态，过精简生活--《断舍离》读书笔记爱吃丸子的小樱桃
不知不觉间房间里的东西越来越多，虽然摆放整齐，但也时常会觉得空间逼仄，令人心生烦闷。抱着断舍离的态度，我开始阅读《断舍离》这本书，希望从书中能找到一些有效的方法，帮助我实现空间、物品上的断舍离。《断舍离》是日本作家山下英子通过自己的经历、思考和实践总结而成的，整体内涵也从刚开始的私人生活哲学的“断舍离”升华成了“人生实践哲学”，接着又成为每个人都能实行的“改变人生的断舍离”，从“哲学”逐渐升华成“
四章-32-点要素的聚合彩云飘过
本文基于腾讯课堂老胡的课《跟我学Openlayers--基础实例详解》做的学习笔记，使用的openlayers5.3.xapi。源码见1032.html，对应的官网示例https://openlayers.org/en/latest/examples/cluster.htmlhttps://openlayers.org/en/latest/examples/earthquake-clusters.
高端密码学院笔记285 柚子_b4b4
高端幸福密码学院（高级班）幸福使者：李华第（598）期《幸福》之回归内在深层生命原动力基础篇——揭秘“激励”成长的喜悦心理案例分析主讲：刘莉一，知识扩充:成功=艰苦劳动+正确方法+少说空话。贪图省力的船夫，目标永远下游。智者的梦再美，也不如愚人实干的脚印。幸福早课堂2020.10.16星期五一笔记:1，重视和珍惜的前提是知道它的价值非常重要，当你珍惜了，你就真正定下来，真正的学到身上。2，大家需要
Day17笔记-高阶函数 ~在杰难逃~ Python 笔记 python 开发语言 pycharm 数据分析
高阶函数【重点掌握】函数的本质：函数是一个变量，函数名是一个变量名，一个函数可以作为另一个函数的参数或返回值使用如果A函数作为B函数的参数，B函数调用完成之后，会得到一个结果，则B函数被称为高阶函数常用的高阶函数：map(),reduce(),filter(),sorted()1.map()map(func,iterable)，返回值是一个iterator【容器，迭代器】func:函数iterab
Day1笔记-Python简介&标识符和关键字&输入输出 ~在杰难逃~ Python python 开发语言大数据数据分析数据挖掘
大家好，从今天开始呢，杰哥开展一个新的专栏，当然，数据分析部分也会不定时更新的，这个新的专栏主要是讲解一些Python的基础语法和知识，帮助0基础的小伙伴入门和学习Python，感兴趣的小伙伴可以开始认真学习啦！一、Python简介【了解】1.计算机工作原理编程语言就是用来定义计算机程序的形式语言。我们通过编程语言来编写程序代码，再通过语言处理程序执行向计算机发送指令，让计算机完成对应的工作，编程
121. 买卖股票的最佳时机薄荷糖的味道_fb40
给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
【JS】执行时长(100分) |思路参考+代码解析（C++） l939035548 JS 算法数据结构 c++
题目为了充分发挥GPU算力，需要尽可能多的将任务交给GPU执行，现在有一个任务数组，数组元素表示在这1秒内新增的任务个数且每秒都有新增任务。假设GPU最多一次执行n个任务，一次执行耗时1秒，在保证GPU不空闲情况下，最少需要多长时间执行完成。题目输入第一个参数为GPU一次最多执行的任务个数，取值范围[1,10000]第二个参数为任务数组长度，取值范围[1,10000]第三个参数为任务数组，数字范围
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
node.js学习小猿L node.js node.js 学习 vim
node.js学习实操及笔记温故node.js，node.js学习实操过程及笔记~node.js学习视频node.js官网node.js中文网实操笔记githubcsdn笔记为什么学node.js可以让别人访问我们编写的网页为后续的框架学习打下基础，三大框架vuereactangular离不开node.jsnode.js是什么官网：node.js是一个开源的、跨平台的运行JavaScript的运行
回溯算法-重新安排行程 chirou_ 算法数据结构图论 c++图搜索
leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
数据仓库——维度表一致性墨染丶eye 背诵数据仓库
数据仓库基础笔记思维导图已经整理完毕，完整连接为：数据仓库基础知识笔记思维导图维度一致性问题从逻辑层面来看，当一系列星型模型共享一组公共维度时，所涉及的维度称为一致性维度。当维度表存在不一致时，短期的成功难以弥补长期的错误。维度时确保不同过程中信息集成起来实现横向钻取货活动的关键。造成横向钻取失败的原因维度结构的差别，因为维度的差别，分析工作涉及的领域从简单到复杂，但是都是通过复杂的报表来弥补设计
基于CODESYS的多轴运动控制程序框架：逻辑与运动控制分离，快速开发灵活操作 GPJnCrbBdl python 开发语言
基于codesys开发的多轴运动控制程序框架，将逻辑与运动控制分离，将单轴控制封装成功能块，对该功能块的操作包含了所有的单轴控制（归零、点动、相对定位、绝对定位、设置当前位置、伺服模式切换等等）。程序框架由主程序按照状态调用分归零模式、手动模式、自动模式、故障模式，程序状态的跳转都已完成，只需要根据不同的工艺要求完成所需的动作即可。变量的声明、地址的规划都严格按照C++的标准定义，能帮助开发者快速
C++ | Leetcode C++题解之第409题最长回文串 Ddddddd_158 经验分享 C++Leetcode 题解
题目：题解：classSolution{public:intlongestPalindrome(strings){unordered_mapcount;intans=0;for(charc:s)++count[c];for(autop:count){intv=p.second;ans+=v/2*2;if(v%2==1andans%2==0)++ans;}returnans;}};
C++菜鸟教程 - 从入门到精通第二节 DreamByte c++
一.上节课的补充(数据类型)1.前言继上节课,我们主要讲解了输入,输出和运算符,我们现在来补充一下数据类型的知识上节课遗漏了这个知识点,非常的抱歉顺便说一下,博主要上高中了,更新会慢,2-4周更新一次对了,正好赶上中秋节,小编跟大家说一句:中秋节快乐!2.int类型上节课,我们其实只用了int类型int类型,是整数类型,它们存贮的是整数,不能存小数(浮点数)定义变量的方式很简单inta;//定义一
Faiss：高效相似性搜索与聚类的利器网络·魚大数据 faiss
Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
【Git】常见命令(仅笔记) 好想有猫猫 Git Linux学习笔记 git 笔记 elasticsearch linux c++
文章目录创建/初始化本地仓库添加本地仓库配置项提交文件查看仓库状态回退仓库查看日志分支删除文件暂存工作区代码远程仓库使用`.gitigore`文件让git不追踪一些文件标签创建/初始化本地仓库gitinit添加本地仓库配置项gitconfig-l#以列表形式显示配置项gitconfiguser.name"ljh"#配置user.namegitconfiguser.email"[email protected]
insert into select 主键自增_mybatis拦截器实现主键自动生成 weixin_39521651 insert into select 主键自增 mybatis delete返回值 mybatis insert返回主键 mybatis insert返回对象 mybatis plus insert返回主键 mybatis plus 插入生成id
前言前阵子和朋友聊天，他说他们项目有个需求，要实现主键自动生成，不想每次新增的时候，都手动设置主键。于是我就问他，那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成，因此为了项目稳定性，不会切换id的生成方式。朋友问我有没有什么实现思路，他们公司的orm框架是mybatis，我就建议他说，不然让你老大把mybatis切换成mybatis-plus。mybat
k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
最超值的Mac——Mac mini 初心么么哒
你知道最超值的Mac是什么吗？自2005年以来，Macmini一直是Apple台式机产品线中的主要产品。最初推出是为了让对Mac好奇的Mac进入Apple生态系统的一种简单方式，现在新的AppleSiliconMacmini可能是任何寻找新Mac的人的最有吸引力的购买。什么是AppleSiliconMacmini？M1Macmini是Apple最小的台式电脑，同时也是最快的台式电脑之一。最新型号由
为什么你总是对下属不满意? ZhaoWu1050
【ZhaoWu的听课笔记】大多数公司，都存在两种问题。我创业四年，更是体会深切。这两种问题就是：老板经常不满意下属的表现；下属总是不知道老板想要什么；虽然这两种问题普遍存在，其实解决方法并不复杂。这节课，我们再聊聊第一个问题：为什么老板经常不满意下属表现?其实，这背后也是一条管理常识。管理学家德鲁克先生早就说过：管理者的任务，不是去改变人。*来自《卓有成效的管理者》只是大多数老板和我一样，都是一边
母亲节如何做小红书营销美橙传媒
小红书的一举一动引起了外界的高度关注。通过爆款笔记和流行话题，我们可以看到“干货”类型的内容在小红书中偏向实用的生活经验共享和生活指南非常受欢迎。根据运营社的分析，这种现象是由小红书用户心智和内容社区背后机制共同决定的。首先，小红书将使用“强搜索”逻辑为用户提供特定的“搜索场景”。在“我必须这样生活”中，大量使用了满足小红书站用户喜好和需求的内容。内容社区自制的高质量内容也吸引了寻找营销新途径的品
辗转相处求最大公约数沐刃青蛟 C++漏洞
无言面对”江东父老“了，接触编程一年了，今天发现还不会辗转相除法求最大公约数。惭愧惭愧！为此，总结一下以方便日后忘了好查找。 1.输入要比较的两个数a,b 忽略：2.比较大小（因为后面要的是大的数对小的数做%操作） 3.辗转相除（用循环不停的取余，如a%b,直至b=0） 4.最后的a为两数的最大公约数 &
F5负载均衡会话保持技术及原理技术白皮书 bijian1013 F5 负载均衡
一.什么是会话保持？在大多数电子商务的应用系统或者需要进行用户身份认证的在线系统中，一个客户与服务器经常经过好几次的交互过程才能完成一笔交易或者是一个请求的完成。由于这几次交互过程是密切相关的，服务器在进行这些交互过程的某一个交互步骤时，往往需要了解上一次交互过程的处理结果，或者上几步的交互过程结果，服务器进行下
Object.equals方法：重载还是覆盖 Cwind java generics override overload
本文译自StackOverflow上对此问题的讨论。原问题链接在阅读Joshua Bloch的《Effective Java（第二版）》第8条“覆盖equals时请遵守通用约定”时对如下论述有疑问： “不要将equals声明中的Object对象替换为其他的类型。程序员编写出下面这样的equals方法并不鲜见，这会使程序员花上数个小时都搞不清它为什么不能正常工作：” pu
初始线程 15700786134
暑假学习的第一课是讲线程，任务是是界面上的一条线运动起来。既然是在界面上，那必定得先有一个界面，所以第一步就是，自己的类继承JAVA中的JFrame，在新建的类中写一个界面，代码如下： public class ShapeFr
Linux的tcpdump 被触发 tcpdump
用简单的话来定义tcpdump，就是：dump the traffic on a network，根据使用者的定义对网络上的数据包进行截获的包分析工具。 tcpdump可以将网络中传送的数据包的“头”完全截获下来提供分析。它支持针对网络层、协议、主机、网络或端口的过滤，并提供and、or、not等逻辑语句来帮助你去掉无用的信息。实用命令实例默认启动 tcpdump 普通情况下，直
安卓程序listview优化后还是卡顿肆无忌惮_ ListView
最近用eclipse开发一个安卓app，listview使用baseadapter，里面有一个ImageView和两个TextView。使用了Holder内部类进行优化了还是很卡顿。后来发现是图片资源的问题。把一张分辨率高的图片放在了drawable-mdpi文件夹下，当我在每个item中显示，他都要进行缩放，导致很卡顿。解决办法是把这个高分辨率图片放到drawable-xxhdpi下。 &nb
扩展easyUI tab控件，添加加载遮罩效果知了ing jquery
(function () { $.extend($.fn.tabs.methods, { //显示遮罩 loading: function (jq, msg) { return jq.each(function () { var panel = $(this).tabs(&
gradle上传jar到nexus 矮蛋蛋 gradle
原文地址： https://docs.gradle.org/current/userguide/maven_plugin.html configurations { deployerJars } dependencies { deployerJars "org.apache.maven.wagon
千万条数据外网导入数据库的解决方案。 alleni123 sql mysql
从某网上爬了数千万的数据，存在文本中。然后要导入mysql数据库。悲剧的是数据库和我存数据的服务器不在一个内网里面。。 ping了一下， 19ms的延迟。于是下面的代码是没用的。 ps = con.prepareStatement(sql); ps.setString(1, info.getYear())............; ps.exec
JAVA IO InputStreamReader和OutputStreamReader 百合不是茶 JAVA.io操作字符流
这是第三篇关于java.io的文章了，从开始对io的不了解-->熟悉--->模糊，是这几天来对文件操作中最大的感受，本来自己认为的熟悉了的，刚刚在回想起前面学的好像又不是很清晰了，模糊对我现在或许是最好的鼓励我会更加的去学加油！： JAVA的API提供了另外一种数据保存途径，使用字符流来保存的，字符流只能保存字符形式的流字节流和字符的难点：a,怎么将读到的数据
MO、MT解读 bijian1013 GSM
MO= Mobile originate，上行，即用户上发给SP的信息。MT= Mobile Terminate，下行，即SP端下发给用户的信息；上行:mo提交短信到短信中心下行:mt短信中心向特定的用户转发短信，你的短信是这样的，你所提交的短信，投递的地址是短信中心。短信中心收到你的短信后，存储转发，转发的时候就会根据你填写的接收方号码寻找路由，下发。在彩信领域是一样的道理。下行业务：由SP
五个JavaScript基础问题 bijian1013 JavaScript call apply this Hoisting
下面是五个关于前端相关的基础问题，但却很能体现JavaScript的基本功底。问题1：Scope作用范围考虑下面的代码： (function() { var a = b = 5; })(); console.log(b); 什么会被打印在控制台上？回答：上面的代码会打印 5。 &nbs
【Thrift二】Thrift Hello World bit1129 Hello world
本篇，不考虑细节问题和为什么，先照葫芦画瓢写一个Thrift版本的Hello World，了解Thrift RPC服务开发的基本流程 1. 在Intellij中创建一个Maven模块，加入对Thrift的依赖，同时还要加上slf4j依赖，如果不加slf4j依赖，在后面启动Thrift Server时会报错 <dependency>
【Avro一】Avro入门 bit1129 入门
本文的目的主要是总结下基于Avro Schema代码生成，然后进行序列化和反序列化开发的基本流程。需要指出的是，Avro并不要求一定得根据Schema文件生成代码，这对于动态类型语言很有用。 1. 添加Maven依赖 <?xml version="1.0" encoding="UTF-8"?> <proj
安装nginx+ngx_lua支持WAF防护功能 ronin47
需要的软件:LuaJIT-2.0.0.tar.gz nginx-1.4.4.tar.gz &nb
java-5.查找最小的K个元素-使用最大堆 bylijinnan java
import java.util.Arrays; import java.util.Random; public class MinKElement { /** * 5.最小的K个元素 * I would like to use MaxHeap. * using QuickSort is also OK */ public static void
TCP的TIME-WAIT bylijinnan socket
原文连接： http://vincent.bernat.im/en/blog/2014-tcp-time-wait-state-linux.html 以下为对原文的阅读笔记说明：主动关闭的一方称为local end，被动关闭的一方称为remote end 本地IP、本地端口、远端IP、远端端口这一“四元组”称为quadruplet，也称为socket 1、TIME_WA
jquery ajax 序列化表单 coder_xpf Jquery ajax 序列化
checkbox 如果不设定值，默认选中值为on；设定值之后，选中则为设定的值 <input type="checkbox" name="favor" id="favor" checked="checked"/> $("#favor&quo
Apache集群乱码和最高并发控制 cuisuqiang apache tomcat 并发集群乱码
都知道如果使用Http访问，那么在Connector中增加URIEncoding即可，其实使用AJP时也一样，增加useBodyEncodingForURI和URIEncoding即可。最大连接数也是一样的，增加maxThreads属性即可，如下，配置如下： <Connector maxThreads="300" port="8019" prot
websocket dalan_123 websocket
一、低延迟的客户端-服务器和服务器-客户端的连接很多时候所谓的http的请求、响应的模式，都是客户端加载一个网页，直到用户在进行下一次点击的时候，什么都不会发生。并且所有的http的通信都是客户端控制的，这时候就需要用户的互动或定期轮训的，以便从服务器端加载新的数据。通常采用的技术比如推送和comet（使用http长连接、无需安装浏览器安装插件的两种方式：基于ajax的长
菜鸟分析网络执法官 dcj3sjt126com 网络
最近在论坛上看到很多贴子在讨论网络执法官的问题。菜鸟我正好知道这回事情.人道"人之患好为人师" 手里忍不住,就写点东西吧. 我也很忙.又没有MM,又没有MONEY....晕倒有点跑题. OK,闲话少说,切如正题. 要了解网络执法官的原理. 就要先了解局域网的通信的原理. 前面我们看到了.在以太网上传输的都是具有以太网头的数据包.
Android相对布局属性全集 dcj3sjt126com android
RelativeLayout布局android:layout_marginTop="25dip" //顶部距离android:gravity="left" //空间布局位置android:layout_marginLeft="15dip //距离左边距 // 相对于给定ID控件android:layout_above 将该控件的底部置于给定ID的
Tomcat内存设置详解 eksliang jvm tomcat tomcat内存设置
Java内存溢出详解一、常见的Java内存溢出有以下三种： 1. java.lang.OutOfMemoryError: Java heap space ----JVM Heap（堆）溢出JVM在启动的时候会自动设置JVM Heap的值，其初始空间(即-Xms)是物理内存的1/64，最大空间(-Xmx)不可超过物理内存。可以利用JVM提
Java6 JVM参数选项 greatwqs java HotSpot jvm jvm参数 JVM Options
Java 6 JVM参数选项大全（中文版）作者：Ken Wu Email: [email protected] 转载本文档请注明原文链接 http://kenwublog.com/docs/java6-jvm-options-chinese-edition.htm！本文是基于最新的SUN官方文档Java SE 6 Hotspot VM Opt
weblogic创建JMC i5land weblogic jms
进入 weblogic控制太 1.创建持久化存储 --Services--Persistant Stores--new--Create FileStores--name随便起--target默认--Directory写入在本机建立的文件夹的路径--ok 2.创建JMS服务器 --Services--Messaging--JMS Servers--new--name随便起--Pers
基于 DHT 网络的磁力链接和BT种子的搜索引擎架构 justjavac DHT
上周开发了一个磁力链接和 BT 种子的搜索引擎 {Magnet & Torrent}，本文简单介绍一下主要的系统功能和用到的技术。系统包括几个独立的部分：使用 Python 的 Scrapy 框架开发的网络爬虫，用来爬取磁力链接和种子；使用 PHP CI 框架开发的简易网站；搜索引擎目前直接使用的 MySQL，将来可以考虑使
sql添加、删除表中的列 macroli sql
添加没有默认值：alter table Test add BazaarType char(1) 有默认值的添加列：alter table Test add BazaarType char(1) default(0) 删除没有默认值的列：alter table Test drop COLUMN BazaarType 删除有默认值的列：先删除约束（默认值）alter table Test DRO
PHP中二维数组的排序方法 abc123456789cba 排序二维数组 PHP
<?php/*** @package BugFree* @version $Id: FunctionsMain.inc.php,v 1.32 2005/09/24 11:38:37 wwccss Exp $*** Sort an two-dimension array by some level
hive优化之------控制hive任务中的map数和reduce数 superlxw1234 hive hive优化
一、控制hive任务中的map数: 1. 通常情况下，作业会通过input的目录产生一个或者多个map任务。主要的决定因素有： input的文件总个数，input的文件大小，集群设置的文件块大小(目前为128M, 可在hive中通过set dfs.block.size;命令查看到，该参数不能自定义修改)；2.
Spring Boot 1.2.4 发布 wiselyman spring boot
Spring Boot 1.2.4已于6.4日发布，repo.spring.io and Maven Central可以下载(推荐使用maven或者gradle构建下载)。这是一个维护版本，包含了一些修复small number of fixes,建议所有的用户升级。 Spring Boot 1.3的第一个里程碑版本将在几天后发布，包含许多

ACM2021辽宁省赛：CDEFGILM